提高组
A. 丹钓战
直接做,对于每个位置求出后面那个弹掉它的位置,容易发现不管询问的开始位置在哪,这个都会被那个弹掉。然后从左端点开始每次跳到下一个弹空的位置,直到右端点,跳的次数就是答案。倍增或者离线排序并查集即可,后者上个基排就是线性。
B. 讨论
考虑枚举一个元素,把所有包含它的集合拿出来,按大小从小到大排序,如果有大小相同的,随便用个啥去重一下,去重之后这两个肯定不相互包含。接下来只需要判断是不是每一个包含前一个,如果是那么这个形成了一条偏序链,这里必然无解,否则我们直接就找到了一个解。看起来需要回答\(O(m)\)次 一个集合是否包含另一个 这样的问题。
爆力做法是根号分治。对于超过根号的我们直接爆力和所有集合都跑一遍,对于不超过根号的我们可以现跑。
能否进一步优化?注意到如果一个集合包含另一个,那么我们会查询小集合的大小次,如果我们可以把复杂度做到只跟小集合的大小相关那就成功了。直接枚举小集合的元素,在大集合中反复二分查找看是否出现就行了,从小到大处理并限制二分长度可以获得一定的常数优化。换个hash table可以做到期望线性。
C. 如何正确地排序
看起来是说,有四个序列,求(所有(两个点的和的min)的和)和(所有(两个点的和的max)的和)的和。
显然min和max是对偶的。这里考虑max。
考虑我们枚举哪个是max,比如是第一个序列,那么我们枚举一个位置\(i\),要计算它的贡献,设\(x_k=a_{k,i},y_k=a_{k,j}\),其中\(j\)是我们要算的那个和\(i\)拼起来之后第一个序列中取到max的另一个位置,那么问题是要限制\(x_1-x_2>y_1-y_2,x_1-x_3>y_1-y_3,x_1-x_4>y_1-y_4\)。问题变成静态三维偏序,总复杂度是\(O(nm\log^2 n)\)。
然后据说可以一个\(\log\),考虑一下。注意到这个题是min+max,我们对max做min-max容斥,然后注意到三项的min和max居然离奇抵消了,所以就变成一堆二维偏序了。
普及组
A. 模拟。
B. 数学游戏
kdw秒了,但是我不理解。
考虑一个素因子\(p\),我们得到\(z=x+y+\min(x,y)\)。也就是说现在我们知道\(x,z-x=y+\min(x,y)\),要求\(y\)。重新设\(z=z-x\)。
看起来这是一个带\(\min\)的方程组,我们应该如何解呢/yun,如果希望在\(\log\)时间内解决这个问题,除了乘除之外我们的工具只有\(\gcd,\operatorname{lcm}\),也就是说我们只能计算一个包含\(+,-,\min,\max,\frac{1}{c}\)的式子。
讨论就行了。当\(x\leq y\),我们得到\(z=y+x,y=z-x\)。当\(x\geq y\),我们得到\(z=2y,y=\frac{z}{2}\)。
考虑如何才能搞出一个东西,它在\(x\leq y\)的时候得到\(z-x\),在\(x\geq y\)的时候得到\(\frac{z}{2}\)。这个\(\frac{1}{2}\)看起来不是很好,我们最后开根号,问题变成凑一个\(2z-2x,z\)。注意到这个分段函数在\(x\)较小的时候是\(2z-2x\),较大的时候是\(z\),而这两段是相交的,并且看起来是下凸的,于是我们所要的东西就是(扔掉范围限制后)两段的\(\max\),如果你不是很理解可以看看这个图的感觉 :
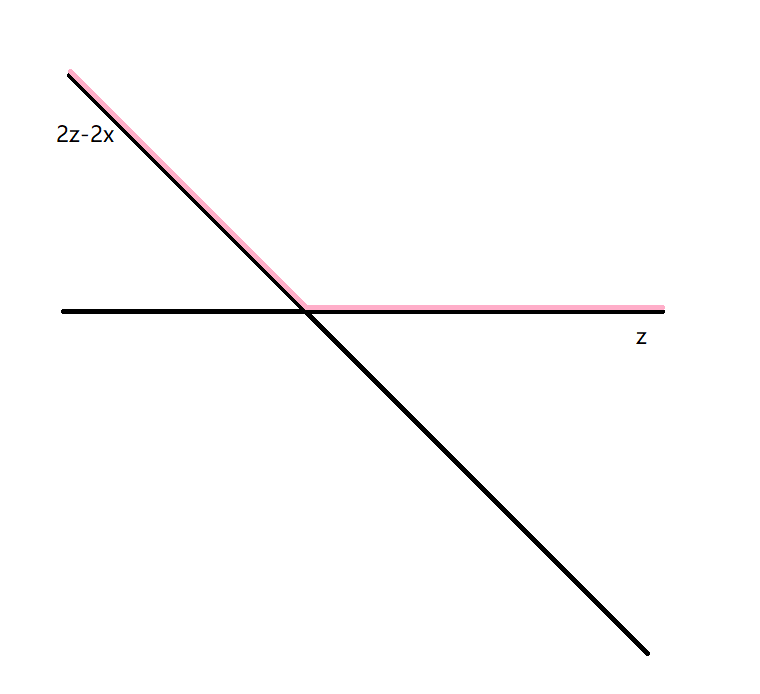
,然后你应该就大概理解了。所以答案就是\(\sqrt{\operatorname{lcm}(\frac{z^2}{x^2},z)}\),但是现在还有问题,也就是\(x\)不一定整除\(z\),并且这个不知道会不会爆精度,所以我们把它改成\(\sqrt{\frac{z\operatorname{lcm}(z,x^2)}{x^2}}\)。然后就无敌了。
这个题是不是比较的mo啊/yun
C. 字符串
直接dp。设\(dp(i,j,k)\)表示前\(i\)次操作使得\(r\)前面有长\(j\)的无用段,然后有长\(k\)的有用段(也就是钦点后面不再会被删了),然后有长\(p_i-j-k\)的无用段,其中\(p_i\)是前\(i\)次操作后剩下的字符个数,也就是前\(i\)次操作中字符的数量减去减号的数量。如果接下来是一个减号,则决策是删开头还是结尾,并且不能删有用的;如果接下来是一个字符,则决策它无用还是有用,只有后面无用段为空并且这个字符恰好匹配才能有用。复杂度\(O(n^3)\)。