海草。海草。
Semi-local string comparison: Algorithmic techniques and applications 的翻译,以及一些oi里的例题。
monge, unit-monge, simple unit-monge
现在有一个矩阵$M$,它的下标是整数。定义它的分布矩阵$M^\square$是它的二维差分。这里分布矩阵的下标是整数$+\frac{1}{2}$,称为半奇数,用带帽的变量如$\hat i,\hat j$表示,并记$i^+=i+\frac{1}{2},i^-=i-\frac{1}{2}$,这里$i$也可能是$\hat i$。那么这个二维差分的具体定义就是$M^\square(\hat i,\hat j)=M(\hat i^+,\hat j^-)+M(\hat i^-,\hat j^+)-M(\hat i^-,\hat j^-)-M(\hat i^+,\hat j^+)$。
现在有一个分布矩阵$M$,它的密度矩阵$M^\Sigma$是它的二维前缀和,具体就是$M^\Sigma(i,j)=\sum_{\hat i<i,\hat j<j}M(i,j)$。
如果我们把$(0,0)$这个位置写在左上角,那么这个二维前缀和就是左下方的二维前缀和。看看dengyaotriangle的slide里的图:
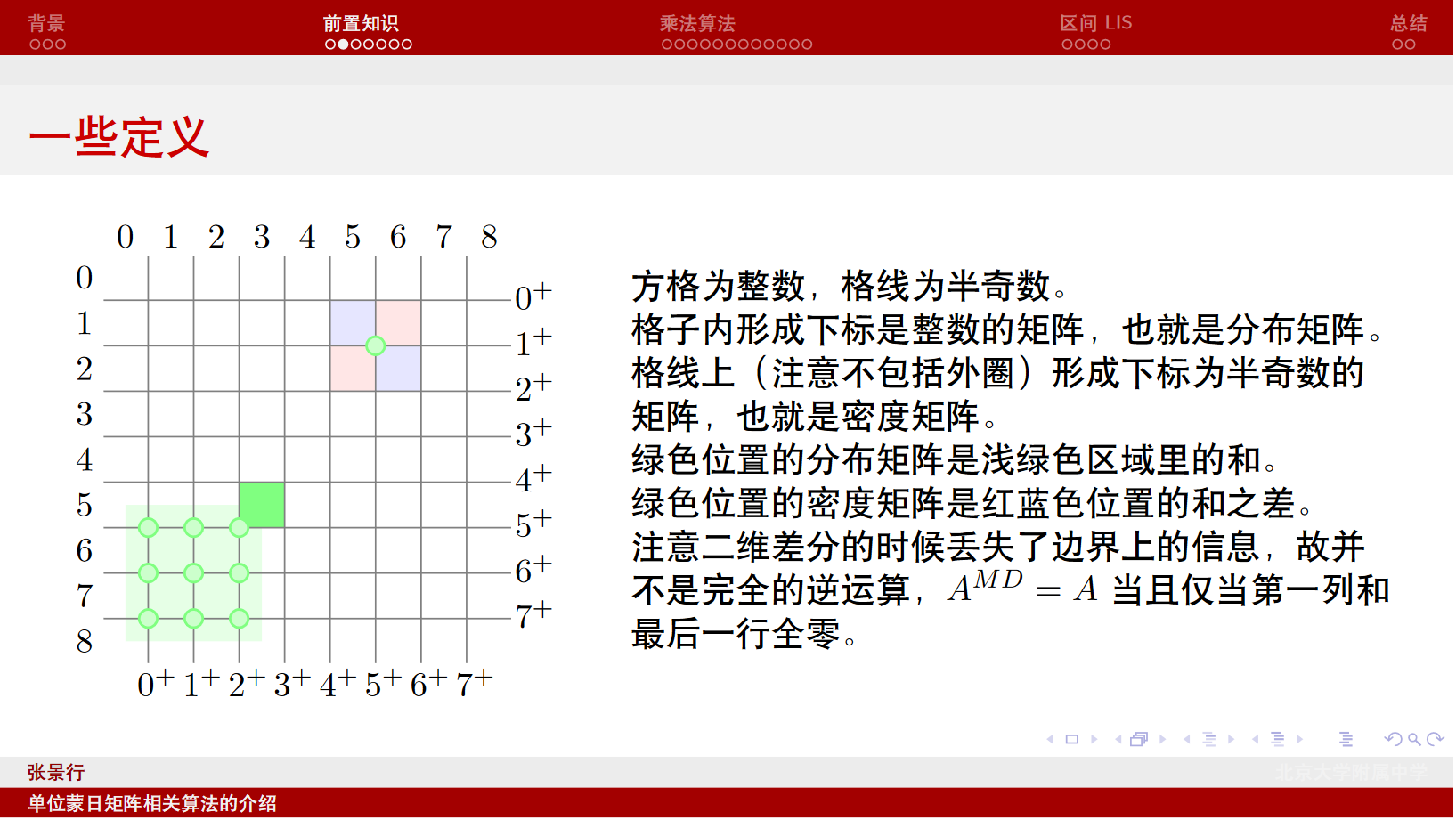
一个下标是整数的矩阵是simple 简单的,当且仅当它的$\square$的$\Sigma$就是它,也就是说它的第一列和最后一行全$0$。
一个矩阵是monge 蒙日的,当且仅当它的$\square$非负。
一个矩阵是unit-monge 单位蒙日的,当且仅当它的$\square$是排列矩阵。一个矩阵是subunit-monge 亚单位蒙日的,当且仅当它是一个亚排列矩阵(允许一些行/列没有$1$的排列矩阵)的$\Sigma$。
以下用$A\times B=C$,或$A^\square\boxdot B^\square=C^\square$表示矩阵乘法。
几个简单结论是,monge矩阵,unit-monge矩阵,subunit-monge矩阵,simple矩阵,对乘法都是封闭的。monge矩阵的和还是monge矩阵,simple矩阵的和还是simple矩阵,因为$\square$是线性变换,但(sub)unit-monge显然不满足这个。
monge矩阵乘法可以二维决策单调性做到$O(n^2)$,也就是 石子合并。如果可以$O(1)$查询一个位置,那么monge矩阵乘向量可以smawk做到$O(n)$。用$\square$表示的simple (sub)unit-monge乘法可以做到$O(n\log n)$;不管是否simple,只要(sub)unit-monge,乘向量都可以$O(n)$。如果不simple的话,矩阵乘矩阵就不好做了。
以下对于(sub)unit-monge矩阵$A$,我们会用到记号$P_A=A^\square$。一般用每行那个$1$的列下标表示$P_A$。
一些基本的东西
unit-monge乘法的封闭性:
所以怎么做乘法??
给定$P_A,P_B$,$A=P_A^\Sigma,B=P_B^\Sigma$是simple unit-monge的,要算$P_C$满足$P_C=P_A\boxdot P_B$,或者说$C=A\times B$。
如果想$O(n\log n)$,先猜可以分治,所以我们分治;但是多少也得有点根据吧,我们看看$C$的定义
\[C(i,j)=\min_k A(i,k)+B(k,j)\]取$m=\lfloor\frac{n}{2}\rfloor$,把$k$分成两部分$k\leq m,k\geq m$,所以我们就把$A$分成了左右两部分$A_{lo},A_{hi}$,$B$分成了上下两部分$B_{lo},B_{hi}$。(这里$m$确实被同时分到两边了,但其实我们是操作$P_A,P_B$,你想象一下,确实应该同时把$m$分到两边。)
对应地把$P_A$分成左右两半$P_{A,lo},P_{A,hi}$(列标号在$[1^+,m^-],[m^+,n^-]$),$B$分成上下两半$P_{B,lo},P_{B,hi}$,定义$P_{C,lo}=P_{A,lo}\boxdot P_{B,lo},P_{C,hi}=P_{A,hi}\boxdot P_{B,hi}$。
Theorem 3.4 若$P_A\boxdot P_B=P_C$,$P_A$的第$\hat k$行全为$0$,则$P_C$的第$\hat k$行也全为$0$。同理,若$P_B$的第$\hat k$列全为$0$,则$P_C$的第$\hat k$列也全为$0$。
Proof 考虑$P_A$的第$\hat k$行全为$0$,等价于$A$的$\hat k^-,\hat k^+$两行是一样的,那么我们乘出来,$C$的这两行肯定也是一样的,所以$P_C$的$\hat k$行也全为$0$。
所以$P_{C,lo},P_{C,hi}$可以递归求出,也就是把$A_{lo},A_{hi}$的全零行和$B_{lo},B_{hi}$的全零列删掉再递归,递归完了再把这些行列插回去。
但是这里$P_{C,lo},P_{C,hi}$其实并不是我们一开始想要的那些项,因为直接把$P_A$分成左右两半,$P_{A,lo}^\Sigma$确实是$A_{lo}$,但$P_{A,hi}^\Sigma$并不是$A_{hi}$,它在$\Sigma$的时候应该考虑$A_{lo}$中的项,但是我们没有这么做。同理$P_{B,lo}^\Sigma$也不是$B_{lo}$。
还好这里我们忽略了的部分的影响是容易考虑的。记$M_{lo}(i,j)=\min_{k\leq m}A(i,k)+B(k,j),M_{hi}=\min_{k\geq m}A(i,k)+B(k,j)$是我们本来想要的东西,那么现在我们要用已经计算出的$P_{C,lo},P_{C,hi}$表示$M_{lo},M_{hi}$。
仔细瞪这个式子:
\[M_{lo}(i,j)=\min_{k\leq m}A_{lo}(i,k)+B_{lo}(k,j)\]刚才说问题出在$B_{lo}$并不是$P_{B,lo}^\Sigma$,要修这个问题,因为$\Sigma$是二维前缀和,有$B_{lo}(i,j)=P_{B,lo}^\Sigma(i,j)+P_{B,hi}^\Sigma(m,j)$。所以
\[\begin{aligned} M_{lo}(i,j)&=\min_{k\leq m}P_{A,lo}^\Sigma(i,k)+P_{B,lo}^\Sigma(k,j)+P_{B,hi}^\Sigma(m,j)\\ &=P_{C,lo}^\Sigma(i,j)+P_{B,hi}^\Sigma(m,j) \end{aligned}\]然后还可以注意到$P_{B,hi}^\Sigma(m,j)=P_{C,hi}^\Sigma(0,j)$,因为
\[P_{C,hi}^\Sigma(0,j)=\min_{k\geq m}P_{A,hi}^\Sigma(0,k)+P_{B,hi}^\Sigma(k,j)\]因为$\Sigma$是左下方的点数,$P_{A,hi}^\Sigma(0,k)$在$k$增加$1$时也增加$1$,$P_{B,hi}$在$k$增加$1$时最多减少$1$,所以$\min$里面的东西随$k$增加是单增的,所以这个$\min$必然在$k=m$处取得,此时$P_{A,hi}=0$,所以就有$P_{B,hi}^\Sigma(m,j)=P_{C,hi}^\Sigma(0,j)$。那么代回上面的式子,我们知道$M_{lo}(i,j)=P_{C,lo}^\Sigma(i,j)+P_{C,hi}^\Sigma(0,j)$。
同理有$M_{hi}(i,j)=P_{C,hi}^\Sigma(i,j)+P_{C,lo}^\Sigma(i,n)$。
现在我们要考虑$P_C^\Sigma(i,j)=\min(M_{lo}(i,j),M_{hi}(i,j))$,那么直接设$\delta(i,j)=M_{lo}(i,j)-M_{hi}(i,j)$,根据$\delta$的符号来判断$\min$取哪边。代入上面算出来的东西,得到
\[\begin{aligned} \delta(i,j)&=P_{C,lo}^\Sigma(i,j)+P_{C,hi}^\Sigma(0,j)-P_{C,hi}^\Sigma(i,j)-P_{C,lo}^\Sigma(i,n)\\ &=(P_{C,hi}^\Sigma(0,j)-P_{C,hi}^\Sigma(i,j))-(P_{C,lo}^\Sigma(i,n)-P_{C,lo}^\Sigma(i,j)) \end{aligned}\]还是从$\Sigma$是左下方点数的角度考虑,我们知道$P_{C,lo}^\Sigma(i,n)-P_{C,lo}^\Sigma(i,j)$就是$P_{C,lo}^\Sigma$中$(i,j)$右下方的点数,$P_{C,hi}^\Sigma(0,j)-P_{C,hi}^\Sigma(i,j)$就是$P_{C,hi}^\Sigma$中$(i,j)$左上方的点数,这个式子就是后者减前者。看一下论文里的图,我们把$P_{C,lo}^\Sigma$中的点标为红的,$P_{C,hi}^\Sigma$标为蓝的,那么$\delta$就是左上方蓝点数减去右下方红点数。
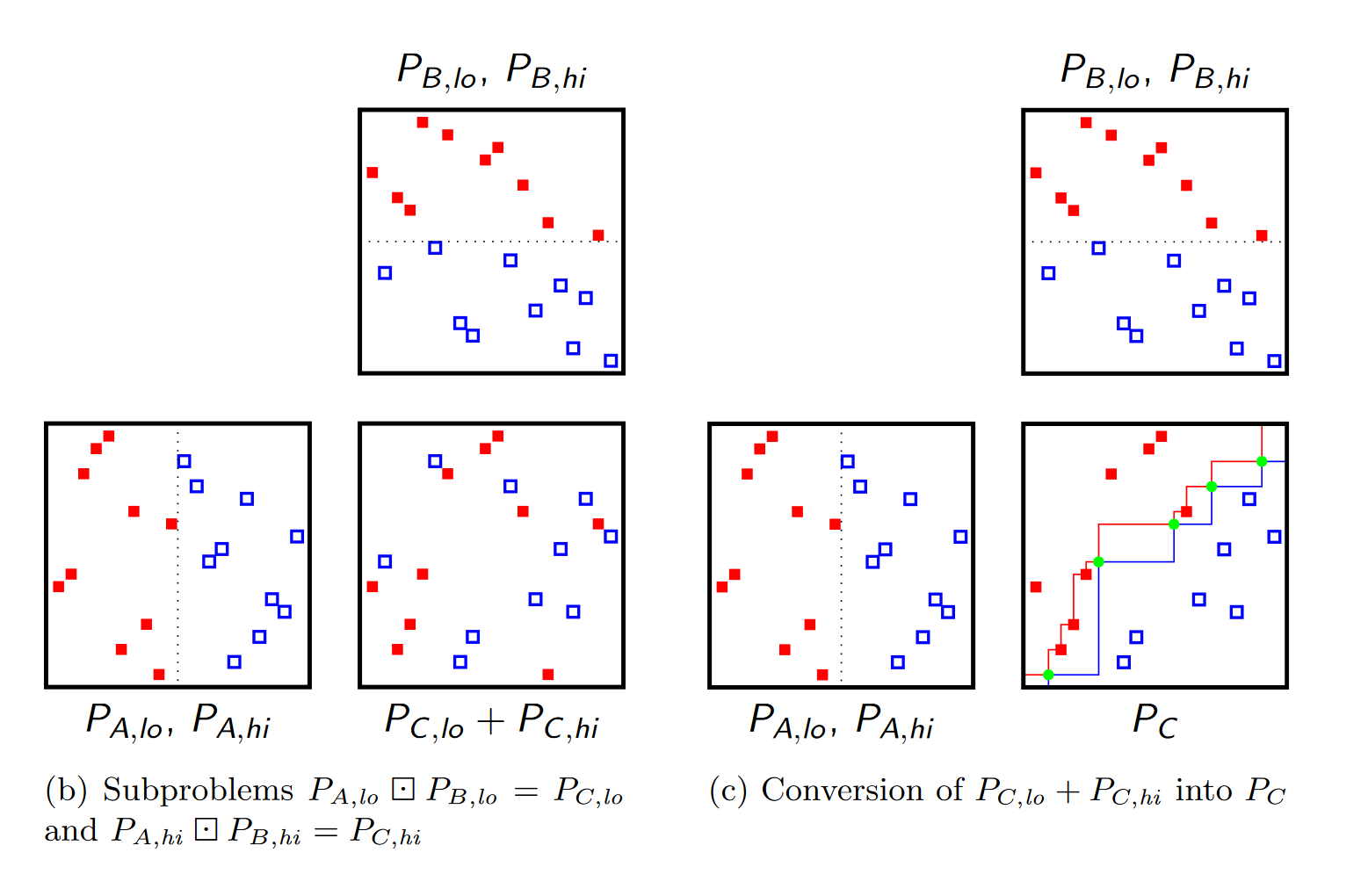
注意到$P_{C,lo}+P_{C,hi}$的和是一个排列矩阵,因为我们递归之后,把子问题的答案拿上来又插了一堆空行/列,而根据我们生成的子问题,$P_{C,lo}$插的空行/列恰好是$P_{C,hi}$非空的那些,反之亦然。
所以我们知道$\delta$的相邻两项差不超过$1$。
然后显然$\delta(i,j)$关于$i,j$都是单增的,因为左上方蓝点数随$i,j$单增,右下方红点数则单减,差肯定还是单增的。所以我们知道可以画两条单调的分界线把$\delta$分成$<0,=0,>0$的三部分。
双指针求出这两条分界线。只需要每次移动一步,维护$M_{lo},M_{hi}$,根据定义容易做到每次$O(1)$。然后考虑怎么求出$P_C(\hat i,\hat j)$。
如果$\delta(\hat i^+,\hat j^+)\leq 0$,那么根据单调性,$(\hat i^+,\hat j^+),(\hat i^+,\hat j^-),(\hat i^-,\hat j^+),(\hat i^-,\hat j^-)$都$\leq 0$。那么我们都可以取$M_{lo}=P_{C,lo}^\Sigma(i,j)+P_{C,hi}^\Sigma(0,j)$,容易知道此时$P_C(\hat i,\hat j)=P_{C,lo}(\hat i,\hat j)$。
如果$\delta(\hat i^-,\hat j^-)\geq 0$则反过来,$P_C(\hat i,\hat j)=P_{C,hi}(\hat i,\hat j)$。
现在只剩下$\delta(\hat i^+,\hat j^+)>0,\delta(\hat i^-,\hat j^-)<0$的情况。根据单调性和相邻位置最多差$1$,容易知道这四个位置的$\delta$一定是
\[\begin{array}{cc}-1&0\\0&1\end{array}\]这样的。那么两条分界线就交于$(\hat i,\hat j)$这个点。代入$\delta$的定义,四个位置的$C$是
\[\begin{array}{cc}M_{lo}(\hat i^-,\hat j^-)&M_{lo}(\hat i^-,\hat j^+)\\M_{lo}(\hat i^+,\hat j^-)&M_{lo}(\hat i^+,\hat j^+)-1\end{array}\]所以$P_C(\hat i,\hat j)=M_{lo}^\square(\hat i,\hat j)+1=P_{C,lo}(\hat i,\hat j)+1$。由于$P_{C,lo}$是排列矩阵,$P_C$也是排列矩阵,所以$P_C(\hat i,\hat j)$必须是$1$。
那么我们知道$P_C(\hat i,\hat j)=1$当且仅当以下三种情况发生任意一个(事实上也不会发生超过一个):
-
$P_{C,lo}(\hat i,\hat j)=1$,且$(\hat i,\hat j)$不在$=0,>0$分界线的右下方(含分界线本身)。
-
$P_{C,hi}(\hat i,\hat j)=1$,且$(\hat i,\hat j)$不在$<0,=0$分界线的左上方(含分界线本身)。
-
$(\hat i,\hat j)$是两条分界线的公共点。
依此算出$P_C$即可。总复杂度$O(n\log n)$。
semi-local lcs
我们都知道lcs是一个网格状dag上的最长路,也就是说$(i,j)\stackrel{0}{\rightarrow}(i+1,j),(i,j+1)$,如果$a_i=b_j$则还有一条$(i,j)\stackrel{1}{\rightarrow}(i+1,j+1)$。
现在我们要求边界上任意两个点之间的最长路。可以在左边和右边加满边转化成上边任意一个点到下边任意一个点的最长路。这里可以看看那个概要里的图。
答案$A$必然是monge的。考虑我们在上边选择$i,i+1$,下边选择$j,j+1$,要证明$a_{i,j+1}+a_{i+1,j}\leq a_{i,j}+a_{i+1,j+1}$,那么我们找到$i$到$j+1$的路径,$i+1$到$j$的路径,它们必然相交于至少一点,随便取一点,把前后交换,就得到$i$到$j$,$i+1$到$j+1$的一个方案,非常对对吧。但是这里只有$i<j$的情况,如果$i>j$,我们定义$a_{i,j}=j-i$,可以发现这让它是monge的。
不过monge的定义是$\geq$,不过关系不大,把所有数取反就好了。
更进一步的,$b_{i,j}=j-i-a_{i,j}$是单位蒙日的。显然它的$\square$是整数。考虑左边和下边,有$b_{n,j}=0,b_{i,0}=0$,所以它是简单的。继续考虑右边和上边,以右边为例,有$b_{i,n+m}-b_{i+1,n+m}=1-a_{i,n+m}+a_{i+1,n+m}$,那么根据定义有$a_{i,n+m}=a_{i+1,n+m}=m$,上边类似。所以其$\square$的行之和和列之和都是$1$,所以它必然是一个排列,所以$A$是单位蒙日的。看起来补的这部分把它从亚单位蒙日变成了单位蒙日。
试看看! 例题1.7
ur25 C. 装配序列
一个排列循环无穷次,多次查询前缀(严格)lis长度。
显然lis长度不超过$n$,并且循环$n$次则必然到达$n$,那么我们只需要对于每个长度求出最短的前缀即可。
pa20 Tekstówka
容易做到$O(n^2\log n+qn)$,因为海草其实可以做一个串的区间和另一个串的所有前缀,分治一下就好了。
但是还可以$O(n^{2.5}+q\sqrt{n})$。考虑分块,