劲爆题。uoj 差评榜 rk3!我找到的所有题解都好像说了什么又好像什么也没说,所以打算自己胡乱写一个。可能是错的,欢迎交流讨论。
注意 匹配 和 增广 的区别。
我们把链横着放,餐馆放在上面,送餐员放在下面。
先在左边加一个$c,w=\infty$的餐馆保证每个送餐员都能匹配。先考虑$c=1$怎么做。
加入一个送餐员的时候,可能的增广路就是从他走到前面的一个餐馆,而如果选择最短增广路,就不会有负环。加入一个餐馆的时候,没有可能的增广路,负环是替换掉之前的一个餐馆,选择最小的负环就不会产生新的负环。为了方便,以下直接用增广路指加入送餐员时产生的增广路,负环指加入餐馆时产生的负环。
问题是增广可能会进行大量的反悔。
但是画一画可以注意到一个牛逼性质。加入一个送餐员$i$的时候,如果他的增广路经过了反悔边,设其意义是反悔了餐馆$j$和送餐员$k$的匹配(也就是说$j$是右数第一条反悔边的右端点),那么这次增广的影响恰好相当于撤销加入餐馆$j$时增广的负环,并拿$i$和$j$匹配。
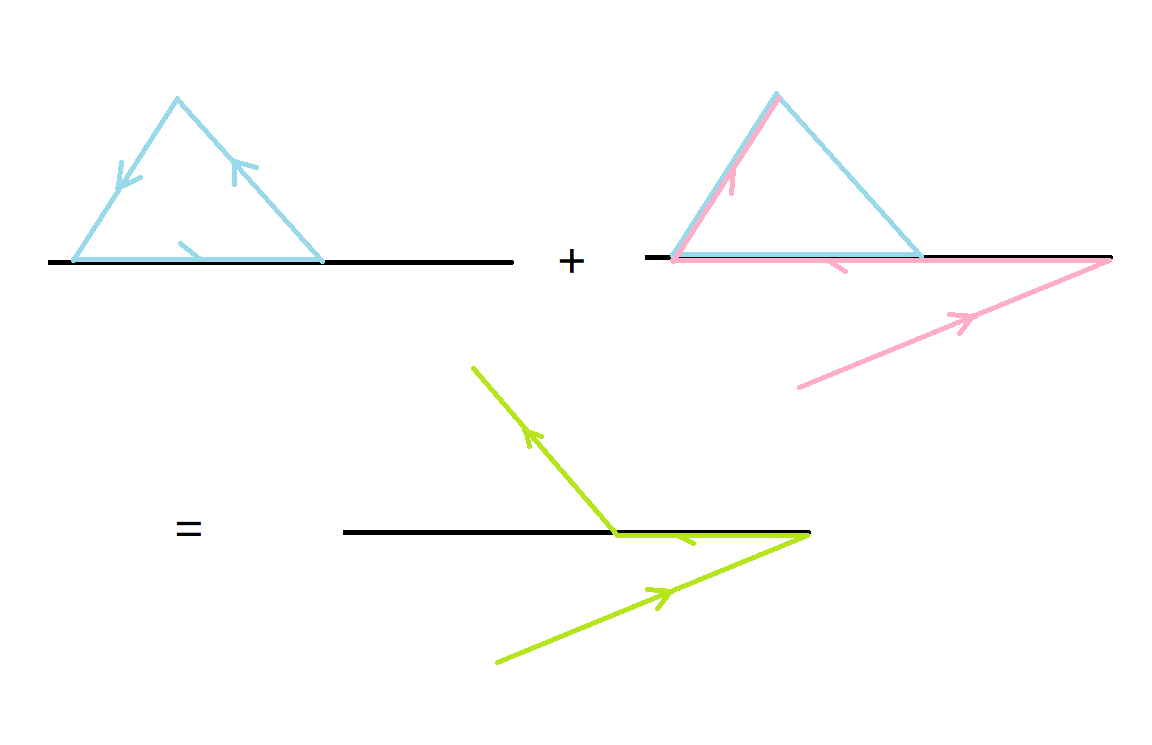
在这个图中,我们的结论体现为,粉色增广路的左半边必然和蓝色负环的左半边重合。
为什么这是正确的?考虑如果前面没有什么变化,它当然是正确的,因为你要匹配$j$,就必须先走一个环把$j$替出,而因为$i$在$j$右边,如果用$j$右边的餐馆替出$j$,相当于$i$匹配了那个餐馆而不是$j$,所以必然是用$j$左边的餐馆替出$j$。而撤销加入$j$时增广的负环,就得到了$j$左边的最优解。由于增广之后$j$左边必然没有流量,$j$左右是独立的,所以$j$左边必然就是加入$j$之前的最优解。
那么问题就是说明前面确实没有什么变化。因为$i$增广的时候$j$到$i$这一段是没有反悔边的,归纳一下,$j$到$i$之间发生的事情就是一些餐馆走了一个负环,一些送餐员直接做了匹配,一些送餐员撤销了最近的负环并做了匹配(根据归纳假设必然是撤销最近的负环)。那么相当于走过的负环形成了一个栈,没有走负环的餐馆形成了一个堆,加入餐馆时如果走了负环会 push 进栈,否则会 push 进堆,而送餐员选择栈顶和堆顶中更优的来 pop。在$j$加入之后栈顶是$j$走的负环,在$i$加入时栈顶又是$j$走的负环,中间的负环都被加入又撤销了,所以这个结论看起来就很对。
这直接给出一个做法,但是看起来跟官方题解做法不太一样,因为官方题解是把栈顶左边向左匹配的餐馆的反悔也扔进堆里了。为了说明这玩意的正确性,注意到不在栈顶的餐馆算的代价只会更大,因为栈中在它上面的餐馆又生成了若干反悔边,而反悔这些边减少的代价并没有被更新。
加入餐馆的时候走负环的性质是类似的。所以可以用两个堆分别维护最优的增广路和负环,复杂度$O(n\log n)$。
具体地。
-
加入一个送餐员。我们在增广路堆中找到堆顶$v$,给答案加上$x+v$,并往负环堆中加入$-(x+v)-x$(提供一个走了反悔边的负环)。
-
加入一个餐馆。我们在负环堆中找到堆顶$v$,如果$v+y+w\geq 0$则没有负环,往增广路堆中加入$-y+w$(提供一个没有走反悔边的增广路);否则给答案加上$v+y+w$,并往增广路堆中加入$-(v+y+w)-y+w$(提供一个走了反悔边的增广路),往负环堆中加入$-(y+w)$(提供一个没有走反悔边的负环)。
对于$c$不一定$=1$的情况,这体现在餐馆会走很多次负环。我们把相同的数合并成一个,也就是额外记一个出现次数,那么负环堆每次只会多$O(1)$个元素,并且增广路堆如果加入了$k$个元素,说明负环堆至少少了$k-1$个元素,所以就有均摊了,复杂度还是$O(n\log n)$。
我感觉这个题可能做了什么双向链大一统之类的事情,毕竟问题性质已经很弱了(虽然不够弱,比如链有容量的时候,或者链上正反边费用不同的时候感觉问题很大),但是我不知道。