basic
我们要构造的是一个$[0,2^k)$的排列,使得相邻两个二进制有恰好一位不同。
可以看成$k$维超立方体上的哈密顿路。
分治,考虑我们现在构造了$[0,2^{k-1})$,那么都添上最高位的$1$就有一个$[2^{k-1},2^k)$的gray code。为了把两边接起来,我们只需要把右边反过来。
注意到第一位总是$0$,最后一位总是$2^{k-1}$,这是一个环。
可以注意到任意长度的gray code都是无穷长gray code的前缀,或者说任意长度的gray code中一个数的位置是不变的。
以下使用reflected gray code特指这个方法。
另一个
考虑$x\operatorname{xor}x+1$,我们会进位若干次然后撞上一个$0$,于是$x\operatorname{xor}x+1$是一个后缀。于是考虑构造一个各位的差分$x\operatorname{xor}(x\operatorname{rsh}1)$,它就变化恰好一位了。写出来可以发现这东西和reflected gray code一致。通过前缀和从reflected gray code得到下标。好像某些牛逼机子可以用指令集完成这个前缀和(可以做系数膜$2$的多项式乘法),一般的机子考虑倍增地做到$O(\log v)$。
ptzsc04 D4 E. Matrix
$2^n\times 2^m$的矩阵,填$[0,2^{n+m})$,使得相邻两个相差不超过一位。
简单题。
scoi2005 超级格雷码
任意进制。
和reflected gray code一样做。
洛谷P7949 ✗✓OI R1 左方之地
相邻两个有恰好$k$位不同。
随机生成想法!考虑我们找到一个每一位到一些$\operatorname{popcnt}=k$的数的双射,猜测直接映射到各连续$k$位是$1$的数即可,继续猜测选的这些线性无关即可,然后根据gray code中相邻两个数哪一位不同来构造答案。
考虑如何证明它是对的。因为线性无关,一个数不会出现两次,所以显然是对的。
agc031c
$[0,2^n)$,钦点两端的数,构造gray code。
为什么你谷上只有绿。
猜测只要两边限制的$\mathrm{popcnt}$的奇偶性不同就有解。考虑设它是$[0,2^n)$,两侧限制是$a,b$,还是分治,如果$a,b$分别在两侧那就随便找一对可以接起来的数递归下去,如果$a,b$在同一侧那就考虑递归这一侧,设我们得到序列$x$,对应到另一侧($\mathrm{xor}$上$2^{n-1}$)是序列$y$,我们像$x_1,y_1,y_2,x_2,x_3,…$这样插起来即可。每次我们会用四个,所以$n=1$会锅,但是$n=1$没必要递归/cf
洛谷P8553 Netzach R1 醒来
任意区间gray code。
出题人多头曾在他的blog写了怎么求$[0,n]$的gray code。考虑设$k$为$2^k<n$的最大的$k$,我们求$[0,k)$的gray code,删掉最高位递归地求$[k,n]$的gray code,然后考虑如何拼起来。注意到我们给gray code全部翻转一位还是gray code,所以不管$[k,n]$的gray code开头长啥样,都能通过翻转$[0,k)$中的对应位把它接上去。复杂度是线性。
那么让我们来看看关键是这个牛逼题应该如何写。可以想到把它在踹上拆成$\log$个子树,但是这里我们不能随便翻转了。
考虑找到最高的那个子树,如果它变化的位是$h$,那么我们把更高的位删掉,把区间划分成$[l,2^h)$和$[2^h,r]$,此时左边都没有$h$位而右边都有,那么如果分别来自两边的两个数相邻,它们$h$以下的位必须相同。
考虑我们把两边怎么拼起来。最简单的想法是直接左边全部取反跑一个前缀gray code,右边跑一个前缀gray code,然后接起来。
问题是如果我们在值域前缀gray code中需要钦点第一个数是$k$的话该怎么做。设我们要求$[0,n]$的gray code,还是按最高位$h$划分。如果$k\geq 2^h$,递归右边之后和没有限制的前缀一样做。如果$k<2^h$,我们直接对左边跑一个reflected gray code并转成$k$在第一位,然后递归右边和左边的最后接起来,这里问题是可能接不起来,因为最后这个数$+2^h$可能没有在右边出现过。于是我们希望这个数尽可能小。使用agc031c的做法,我们知道只要$\mathrm{popcnt}$的奇偶性对了就行,于是总可以让它是$0$或$1$。如果它是$1$我们可能接不起来,此时$\mathrm{popcnt}$的奇偶性必然不对,而由于右边长度是$1$,根据前面的划分我们知道它不可能接到别的地方去,所以就是无解了呢。
xxiii poi stage 3 Klubowicze
$[0,2^n)$分成$2^{n-1}$对,构造一个环,满足相邻两个数要么是一对要么恰好一位不同。
感觉啥性质都没有。还是猜测很容易有解,先猜一个奇偶之间的对有偶数个就有解。强行分治,把左右之间的对先拿出来然后递归,如果没有左右之间的对,这里是个环所以就赢了。
如果有左右之间的对,我们考虑怎么把它们塞进去,发现不考虑它们直接递归,然后硬拼左右两边是在一个一堆三度点的图上找哈密顿回路。手玩一下感觉很复杂。
考虑我们先把左右之间的对们串起来,然后往其中填剩下的。但是这里又有一个顺序的问题。
还是考虑一下复杂的东西是啥。发现我们能串起来,当且仅当在左右之间横跳共偶数次,并且对于每一边,包含在跨过的某对中的点的集合是若干在这边递归得到的环上相邻的对的并。偶数次是好解决的,如果是奇数次或$0$次我们只需要找到$O(1)$个差最高位的对塞进去即可。考虑如何递归下去才能保证后面这个。看看官方题解的图 :
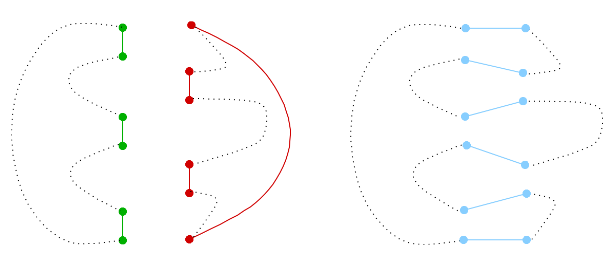
然后你就懂了。我们随便找一个顺序把右图中这些边排序,然后把它们断开,加入左图中实线表示的辅助边,可以发现这样加边之后必然能串起来,而解的存在性也由此归纳证明了。