回去whk了。
咕,因为并不会。
直线
直线是$ax+by=c$,非常建议这么写。可以为直线钦定一个唯一的最简形式,让$a,b,c$中第一个非$0$的是$1$即可。
一个简单的和直线垂直的向量是$d=(a,b)$,可以称作是它的法向量,这是因为直线就是$(x,y)\cdot(a,b)=c$,也就是在法向量上的投影,乘上法向量长度为某个定值的点集。一个和直线平行的向量就是$(-b,a)$。
想象直线的时候可以直接想象其法向量。如果你喜欢,可以整个乘$\frac{1}{\sqrt{a^2+b^2}}$。
某种意义上来说,我们是沿着$d$的方向画了等高线,然后选择其中一条。
可以注意到这个投影长度$\frac{(x,y)\cdot(a,b)}{\vert(a,b)\vert}$和到直线的距离有关,实际上把平面转过来并除一个$\vert (a,b)\vert$就是按照这个距离拍在数轴上,这里我们是把$c$规定为$0$,于是$(x,y)\cdot(a,b)$变成了$(x,y)\cdot(a,b)-c$,当然还要绝对值。于是平行直线距离就是$\frac{\vert c_1-c_2\vert}{\vert(a,b)\vert}$。
圆
到点距离是定值的图形是圆。
到两点距离和/差/商是定值的图形是椭圆/双曲线/(阿氏)圆。
计算几何好像不是很擅长处理交点,一般我们希望不用交点。
圆交好像出的不多。
圆锥曲线
椭圆上的问题先考虑拉伸成圆。
双曲线上的问题可以考虑旋转并拉伸成$xy=k$。
有些问题是不能这么做的,不过它们实在是太奇怪了。
拉伸之后斜率也是可以算的。
离心率
懒得写了。背背得了。
两个圆锥曲线
这样的问题好像不是很多。一般来说你不会希望出现两个圆锥曲线。
定比点差
感觉这个东西很奇怪啊。
一般来说我们会选择一个原点然后建系,把剩下的东西设出来,直线(或者说,共线)和定点看成条件。那么条件是啥决定了我们的各个式子要采取什么形式。定比点差本质上就在干这么一个事情,只不过它可能是总结了一类比较常见的。
比如这里摘录一个题吧 : 椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$,过$P=(4,0)$引一条直线交椭圆于$B,A$,$A^\prime$是$A$关于$x$轴的对称点,证明$A^\prime B$总是过$M=(1,0)$。
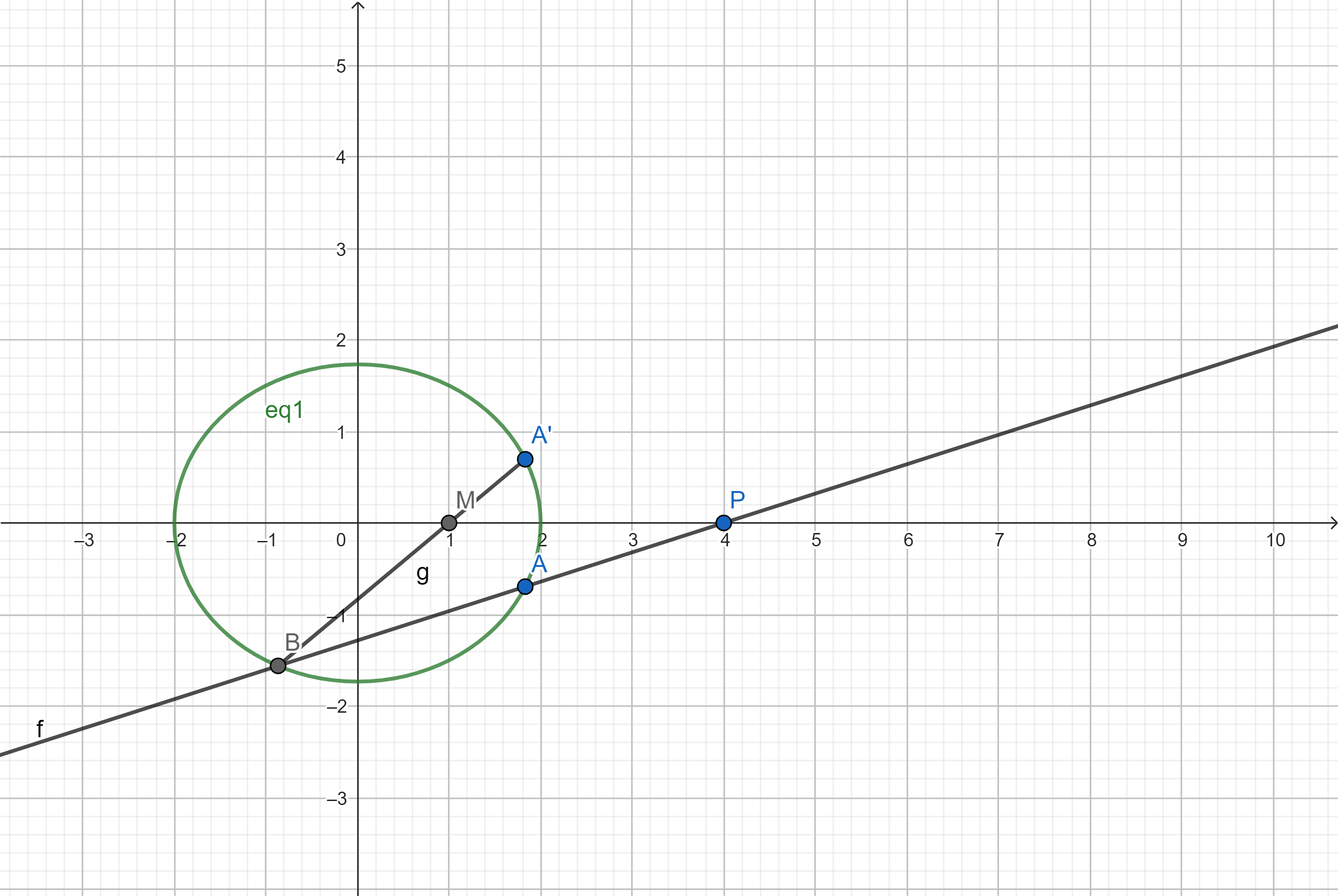
那么考虑从$M$出发建系,设$A=(a,-b)$,$A^\prime=(a,b)$,从$M$考虑的话,$B(\lambda a,\lambda b)$,$P(3,0)$。现在椭圆是$\frac{(x-1)^2}{4}+\frac{y^2}{3}=1$。
看了一眼,可以看到我们已经有了$A,A^\prime$对称,$AB$过$M$,那么剩下的三个东西 : $A$在椭圆上,$B$在椭圆上,$A,B,P$共线,我们需要选两个当条件。如果每个方向上的$AB$过$M$都能确定剩下的部分满足题意,那么反过来题意就可以推出$AB$过$M$。
也就是说我们实际上在尝试搞出这么一个$\Rightarrow$ :
\[\left\{\begin{array}{} \frac{(a-1)^2}{4}+\frac{b^2}{3}=1\\ \frac{(\lambda a-1)^2}{4}+\frac{\lambda^2 b^2}{3}=1\\ \end{array}\right. \Rightarrow \frac{3-a}{a}=-\frac{1-\lambda}{1+\lambda}\]为了让它好看一点,我们把它和$A$在椭圆上的那个式子一减,得到$\frac{a(a+\lambda a-2)(1-\lambda)}{4}+\frac{b^2(1+\lambda)(1-\lambda)}{3}=0$,然后刚才我们知道$1-\lambda=\frac{(a-3)(1+\lambda)}{a}$,于是就是$\frac{(a-3)(a+\lambda a-2)(1+\lambda)}{4}+\frac{(a-3)b^2(1+\lambda)^2}{3a}=0$。此时只有$1+\lambda$了,令它是$t$,就得到$\frac{(a-3)(at-2)t}{4}+\frac{(a-3)b^2t^2}{3a}=0$,去分母并化简就得到$3a^2t^2-6at+4b^2t^2=0$。