做xix open cup遇到了两个平方串题。再写一写,可能这次会比较深刻吧。
square(tandem repetition, repetition, repeat)
定义一个串是平方串,当且仅当它的前一半和后一半相同。它的前一半称作它的平方根或简称根。
类似地可以定义立方串,四次方串……但是它们意义不是很大。
boi2004 repeats
求一个串的子串的最高次数,并输出所有具有这一次数的子串。
给出一个求所有重串的做法。从大到小枚举根的长度\(l\),然后按\(l\)大小分块,那么根一定是一个块前缀和一个块后缀。用sa求出相邻两块的lcp和lcs,然后就得到一个区间的重串,这里还是画一下吧 :
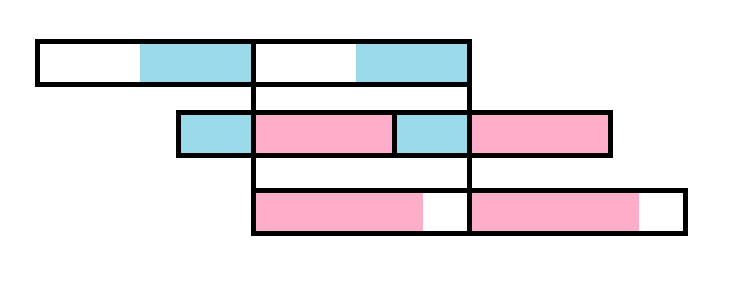
然后为了求出连续重复次数,我们可以直接在这个上面尝试继续扩展,也就是把相同的块直接连起来,在两边尝试上面的东西。写起来并不困难。
noi2016 优秀的拆分
求所有子串划分成形如AABB的串的方案数之和。
我们枚举一个拆分,也就是枚举两个相邻的重串这样的,那么问题是求出每个位置作为开头和结尾的重串数量。套用上个题的做法即可。
zjoi2020 字符串
求区间平方串个数。
长\(2k\)的平方串贡献一个矩形,长\(2k\)的一个平方串区间贡献一串矩形。这是一个经典问题,我们拿两条斜线容斥一下就好了,具体见command_block在洛谷的题解。所以转化成平行于\(x=y\)的斜线加,右下2-side矩形求和,发现左下2-side矩形比较好做,分开考虑包含的和经过边界的斜线即可。复杂度\(O(n\log^2 n)\)。
xix open cup, gp of gomel C. Three Indices
用若干个区间和长度表示所有允许\(1\)的汉明距离的平方串,具体地,允许左右两边最多一次出现对应位置不同。
这个被称为 approximate tandem repeatition。
考虑一个允许\(1\)的汉明距离的sa,我们求一个lcp,跳过一个不同字符,然后再求一个lcp即可。统计答案的时候,枚举两边有多少不同的卷起来即可。
可以扩展到允许\(k\)的距离,复杂度将是\(O(nk\log n)\)。
run
注意到上面的方法说明相同长度的平方串形成若干个区间。定义一个run(译名好像是 顶天立地串/kx)是一个周期\(p\)和极长的以这一周期作为最小周期的子串\([l,r]\)组成的二元组(但是我会记为\((l,r,p)\)),显然它表示了一堆平方串。定义一个串的runs是它的所有run的集合。
The runs theorem 一个串中run的个数不超过\(n\)。
定义一个run的根是它里面任意一个长\(p\)的子串。如果我们找到了一个run的一个根,那么可以向两边爆力扩展,下面的结论说明了这样做的复杂度 :
The runs theorem 定义一个run的指数是\(\frac{r-l+1}{p}\)。一个串中run的指数和不超过\(3n-3\)。
但是一般我们不会这么做,因为一次lcp一次lcs就可以实现向两边扩展了。
如果我们求出了所有run,那么很容易枚举所有平方串。枚举一个长度\(2kp\)即可。
lyndon word
接下来我们描述lyndon word的理论。
一个串是lyndon串,当且仅当它比所有非平凡后缀都小,或者说它是所有循环同构中严格最小的。按照定义,aaaaa不是lyndon串,但是a是。
接下来我们考虑lyndon串的结构。
显然 如果lyndon串\(w=uv\),那么\(u<v\)。
定理1 一个串\(w\)是lyndon串,当且仅当它是单字符,或者它可以分解成两个lyndon串\(w=uv\),其中\(u<v\)。
证明 \(\Leftarrow\) : 考虑所有后缀。
\(\Rightarrow\) : 找到\(w\)的最小真后缀,那么根据定义它是lyndon串,直接令它为\(v\),剩下的部分为\(u\)。接下来证明\(u\)是lyndon串,考虑\(w\)比\(w\)的任意后缀小,而\(u\)比\(w\)小,所以\(u\)比\(w\)的任意后缀小,而\(v\)是\(w\)的最小真后缀,在\(w\)的一个后缀中把\(v\)替换成空对大小不会有影响,而把\(v\)替换成空就变成了\(u\)的后缀,所以\(u\)比\(u\)的任意后缀小。
定义一个lyndon串的标准分解是最小真后缀和剩下的部分。分解形成一棵树,可以猜到这是它的sa的笛卡尔树。
lyndon root
显然由于run的周期是最小周期,我们知道每个run必有一个lyndon串作为它的根,称为lyndon根。接下来我们指出lyndon根的重要性质。
引理1 设\(w=u^ku^\prime a\),其中\(u\)是lyndon串,\(a\)是一个字符,\(u^\prime\)是\(u\)的极长前缀(可能为空),也就是向后加入\(a\)的话则不再是\(u\)的前缀。设\(u\)中\(u^\prime\)之后的字符是\(c=u_{\vert u^\prime\vert+1}\)。则
-
如果\(a>c\),那么\(w\)是一个lyndon串。
-
如果\(a<c\),那么以\(w\)为前缀的串的最长lyndon前缀必然是\(u\)。
证明 很直接。
-
如果\(a>c\),那么显然。
-
如果\(a<c\),那么显然。
反复阅读你就懂了(
所以我们知道,从左往右扫原串,如果遇到了case 2,那么这个run的lyndon根必然是原串一个后缀的最长lyndon前缀,这个数组称为lyndon数组,而我们马上会描述求这个东西。为了稳定遇到case 2,我们可以把字典序反过来再做一遍,这样正序和反序下的lyndon array必然有一个给出了lyndon根(,实际上,容易发现另一个总是给出长\(1\)的平凡lyndon串,所以实现起来更为简单了)。这实在是比较的离奇。
lyndon分解, lyndon array
定义一个串的lyndon分解是极小的划分成若干lyndon串的方案。根据定理1,极小当且仅当这些lyndon串是从大到小排列的。容易证明lyndon分解唯一,这说明我们可以按照定理1以任意顺序尽可能合并得到lyndon分解。
定理2 lyndon分解的第一部分是最长lyndon前缀,最后一部分是最长lyndon后缀。
证明 如果不是最长的,根据lyndon分解唯一,我们知道必然还可以合并。
为了求lyndon数组,我们可以考虑从右往左扫,维护当前后缀的一个极小lyndon串分解。接下来我们会加入一个字符,然后我们不断尝试把这个字符和右边合并,还是根据定理1我们知道合并只需要比较两个lyndon子串的字典序,比较后缀的字典序即可。最多会进行\(n-1\)次合并,所以我们可以使用二分hash做到\(O(n\log n)\),或者sais 四毛子rmq做到\(O(n)\)。
所以我们现在已经会\(O(n)\)算runs了!
二分hash做法的实现收录在我的 板子/Lyndon Array。
本原平方串,三平方串定理(three squares lemma)
定义一个平方串是本原平方串,当且仅当长度的一半是它的最小周期。
三平方串定理 如果三个本原平方串\(uu,vv,ww\),满足\(uu\)是\(vv\)的真后缀,\(vv\)是\(ww\)的真后缀,那么\(\vert u\vert+\vert v\vert\leq\vert w\vert\)。
所以我们知道本原平方串有\(O(n\log n)\)个。一种称为fib字符串的串达到了这个上界,具体可以看oi-wiki的main-lorentz词条。
定理3 对于所有run \((l,r,p)\),其\(r-l-2p\)的和为\(O(n\log n)\)。
证明 一个run中所有长\(2p\)的子串就是所有的本原平方串,其数量为\(r-l-2p+2\),而本原平方串的数量是\(O(n\log n)\)。
接下来是更多关于lyndon串的东西,而和runs关系不大了。
求出一个lyndon分解
duval’s algorithm
根据引理1,我们可以简单地增量求lyndon分解。直接从左往右扫,维护\(u,k,u^\prime\)即可,尝试匹配\(u\),如果不匹配,如果是case 1则\(u:=u^\prime,k:=1\),否则\(u:=\varnothing\)之类的。但是这个做法不能求每个前缀的lyndon分解,需要在串最后加入一个结束符。
sa
刚才在定理1的证明中,我们断言把最小后缀替换成空不影响前面的大小关系,所以可以直接后缀排序,每次选择剩下的部分中的最小后缀,可以知道最后我们选择了sa的前缀\(\min\)。但是这个做法难以对每个后缀求lyndon分解。可能其实居然有点用吧。
jsoi2019 节日庆典
求每个前缀的最小表示。\(n\leq 3\times 10^6\)。
lyndon分解的最后一部分是最小后缀,但是这里是最小表示而不是最小后缀,所以我们要考虑往后接了一个原串之后谁的字典序更小。考虑duval,发现如果我们知道了\(u^\prime\)的lyndon分解就赢了,因为\(u^\prime\)比前面任何后缀都要小,那么我们就直接递归到\(u^\prime\),注意到\(u^\prime\)的长度不超过原串的一半,所以我们同时维护\(\log\)个duval即可。比较两个可能成为答案的后缀,发现如果短的不是长的的前缀,那么由于你在duval,显然是长的更优,如果短的是长的的前缀,画一画发现转化成比较一个后缀和原串,z algo即可。复杂度\(O(n\log n)\)。
这个东西看起来很有趣。发现duval维护的是一个不一定是lyndon分解的最后一部分的东西,它不一定是因为后面可能加入各种字符。这一递归说明这样的东西可能很少,于是我们干脆导出significant suffix,尝试更深刻地描述这些东西的结构。
significant suffix
定义一个串\(s\)的significant suffix,是它接上某一个串之后可能的在\(1,...,\vert s\vert\)中最小的后缀,也就是认为空字符和任何字符不可比,则两两不可比的最小后缀集合,也就是接下来可能作为lyndon分解的最后一部分的位置,看起来似乎也就是duval算法中维护的\(u^ku^\prime\)和对\(u^\prime\)不断递归duval再得到的\(u^ku^\prime\)们。
显然对于任意两个significant suffix,短的是长的的前缀。
定理4 长度相邻的significant suffix \(u,v\),其中\(\vert u\vert>\vert v\vert\),则\(\vert u\vert\geq 2\vert v\vert\)。
证明 不使用引理1来证明它。我们知道,\(u,v\)要么前\(\vert u\vert-\vert v\vert\)个字符相同,要么\(v\)没有这么长。继续推可以知道它们都以\(\vert u\vert-\vert v\vert\)作为周期。设这个周期是\(p\),那么如果\(v\)不完整包含\(p\),显然满足\(\vert u\vert>\vert v\vert\),则\(\vert u\vert\geq 2\vert v\vert\);否则我们知道\(u=ppw,v=pw\),其中\(w\)是某个串。此时由于\(v\)是significant suffix,存在一个\(x\)满足\(pwx<ppwx\)。但是这推出\(wx<pwx\),所以此时\(v\)不是最小后缀,\(w\)比它更小,矛盾了。
jsoi2019 节日庆典
直接尝试维护所有的significant suffix。由于两个significant suffix,短的必然是长的的前缀,所以每次加入一个字符的时候,只需要比较两个字符,求答案和前面那个做法是一样的。
zjoi2017 字符串
区间加,求区间最小后缀。\(n\leq 2\times 10^5,q\leq 3\times 10^4\)。
我们直接在线段树上维护significant suffix。直接保留右儿子所有significant suffix,虽然其中可能有不是significant suffix的串,我们只需要让信息在\(O(\log n)\)即可;左儿子最多有一个串是significant的,我们比较接上右儿子之后哪个最小,如果仍然存在忽略空字符不可比的,根据定理3的证明应该保留其中最长的那个。使用二分hash支持比较两个串,比较的时候需要\(O(\log^2 n)\),复杂度\(O(\log^4 n)\)。可以考虑用类似于多树二分的trick。
为了让它跑的快一点,注意到我们有\(q\log^2 n\)次比较两个串和\(q\)次修改,所以考虑改用根号平衡维护hash值,就可以\(O(\sqrt{n})-O(1)\)了。总复杂度\(O(n\log^2 n+q\log^3 n+q\sqrt{n})\)。