部分译自 On-line construction of compact directed acyclic word graphs。外国看起来更习惯把suffix automaton称为directed acyclic word graph dawg,试译 有向无环字典图。但是我觉得sam就很好听啊(
deepl有点拖拉机了,所以我用了生草机。然后就把au-tomaton翻译成了au番茄。
考虑匹配后缀的爆力数据结构是后缀trie,也就是所有后缀组成的trie。
对这一结构进行 最小化,也就是如果两个点相同字符的转移到达相同的点,那么把它们合并成一个(它们也被视为相同的),直到不能继续合并,就得到sam。
对这一结构进行 压缩,也就是如果一个点只有一个转移,我们把它删掉,把它的转移合并到父亲上去,或者说把极长的没有分叉的链缩成一条边,就得到st。
如果同时进行最小化和压缩,我们就得到compacted sam 压缩sam,或者说 紧致后缀金番茄。
所以显然的构造方法是跑一个sam,然后进行压缩,也就是把极长的没有分叉的链缩成一条边;或者跑一个st,然后进行最小化,不过这个比较复杂。这些很离线,我们考虑点在线的直接构造压缩sam的方法。
在开始工作之前,我们先扯一些定义。
用\(a,b,c\)表示一个字符,\(x,y,z\)表示一个串。以下说到子串默认是我们处理的串\(s\)的子串这样的。
定义\(\mathrm{beginpos}(t),\mathrm{endpos}(t)\)是\(t\)在\(s\)中出现位置的左端点/右端点的集合。众所周知st压缩\(\mathrm{beginpos}\)等价类,sam压缩\(\mathrm{endpos}\)等价类。
但是很遗憾,不完全是这样的,由于ukkonen算法实在是太棒了,我们更通常认为st是ukkonen算法构造的st,它压缩的是一个 \(\mathrm{beginpos}\)相等 的超集\(=_L\),定义为如果\(x\)可以向后增加若干个字符变成\(y\),并且每次加字符都是唯一的(加别的字符得到的都不是原串的子串),则\(x,y\)等价。压缩\(\mathrm{beginpos}\)等价类的st称为 完整后缀树,二者的区别在于,ukkonen的后缀树中,后缀对应的点可能被压进了边里,而完整后缀树不会出现这种情况。
压缩sam压缩\(=_L\)或\(\mathrm{endpos}\)等价类,也就是说两个子串相等当且仅当\(=_L\)或\(\mathrm{endpos}\)相等,或者存在第三个串和它们都相等。另一种你可能更喜欢的说法是,两个串相等当且仅当存在另一个串可以通过 不改变\(\mathrm{endpos}\)的向左扩展 和 唯一的向右扩展 得到这两个串。完整压缩sam压缩\(\mathrm{beginpos}\)或\(\mathrm{endpos}\)等价类。这个听起来有点抽象,我们可以考虑一个性质,每个等价类有且仅有一个最长串,它满足向左/右扩展都会让出现位置变少,所以完整压缩sam的每个点表示一个不能不改变\(\mathrm{beginpos}\)地向右扩展的串的\(\mathrm{endpos}\)等价类,压缩sam的每个点表示一个不能向右唯一扩展的串的\(\mathrm{endpos}\)等价类。
定义上文 left context \(\mathrm{LC}(x)\)是\(t\)的\(\mathrm{endpos}\)等价类中最长的串,\(\mathrm{RC}(x)\)是\(\mathrm{beginpos}\)等价类中最长的串,于是\(\mathrm{endpos}\)等价类就是\(\mathrm{LC}\)等价类这样的。如果你看过集训队论文,你可能会比较知道这些。定义上下文 context \(\mathrm{LRC}(x)=\mathrm{LC}(\mathrm{RC}(x))=\mathrm{RC}(\mathrm{LC}(x))\)。这些东西在后文中可能甚至不会出现,但是可以注意到上/下文和等价类是一个东西,所以有时候你可能可以考虑把等价类转化为上/下文来提供一个比较直观的东西。
这个构造紧致后缀金番茄的算法基于ukkonen的后缀树算法,所以我们先介绍它。
后缀树,Ukkonen算法
结论 如果一个串的所有非空后缀中,任意两个都没有一个是另一个的前缀,那么\(=_L\)和\(\mathrm{beginpos}\)相等是相同的等价关系。
所以通过向串的最后加入一个串中不存在的字符,得到的必然是一棵完整后缀树。但是有些时候我们并没法这么做,比如需要考虑每个前缀的st的时候,这就需要胡乱搞一搞了。
ukkonen算法所建立的后缀树定义为 :
-
每个点代表一个\(=_L\)等价类中的最长串。如果一个子串不对应一个点,或者说它不是等价类中的最长串,称它是一个隐式结点。否则它是一个显式结点。当我们说到点的时候,默认它是一个显示结点。为了记录一个隐式结点,我们可以使用三元组\((u,c,p)\),指从它的第一个显式父亲\(u\)出发,\(c\)开头的边上第\(p\)个位置对应的点。
-
每条边从一个点\(x\)连向另一个点\(xy\),其中\(xy=\mathrm{RC}(xa)\),\(a\)是一个字符;边上的串是\(y\)。这里\(y\)必然是原串的一个子串,所以我们用一个区间表示它。
说人话就是把后缀trie上的单链缩起来。
考虑向右增量建立后缀树,要求复杂度\(O(n)\)。
我们需要给每个原来的后缀向后扩展一个字符。如果一个后缀是个叶子,那么这相当于让它的父边向后扩展一位,我们直接将叶子的父边写成\([l,\infty]\)这样的就好了。如果一个原来的后缀不是一个叶子,那么我们需要把扩展的字符建出来。不过也有可能它本来就有这么一条出边,此时我们就啥也不用干。如果我们在扩展一个后缀的时候,把新字符建了出来,则称为一次 显式扩展,否则是 隐式扩展。
可以注意到一个后缀从内部结点扩展成叶子之后它就永远是叶子了,所以每个后缀只会显式扩展一次,所以爆力扩展复杂度就是正确的,所以考虑什么样的后缀被显式扩展了。一个后缀被显式扩展,当且仅当它不是一个叶子,并且它没有新字符开头的出边。
-
考虑什么样的后缀不是一个叶子。显然一个点不是叶子,当且仅当有一个字符可以接到它后面,而后缀后面就是空了,所以它不是叶子当且仅当它在串中还有另一次出现(除了在末尾的那一次)。可以注意到长的后缀出现次数不会比短的多,所以我们找到最长的出现至少两次的后缀,称为 最长重后缀,设它的长度是\(l\),那么所有长度\(\leq l\)的后缀都不是叶子,\(>l\)的都是叶子。
-
考虑 本来就有这么一条出边 的情况,可以注意到如果一个后缀有一条\(c\)开头的出边,那么比它短的后缀都有一条\(c\)开头的出边,所以也是长度\(\leq\)某个数的所有后缀是有的,剩下的都没有。
所以我们知道必然是一个长度区间的后缀需要显式扩展。
为了枚举这些后缀,我们考虑从最长重后缀开始向下枚举,也就是每次找到当前串的最长真后缀对应的点,称为它的suffix link。问题是如何求这个suffix link。
首先一个显式结点的suffix link必然指向一个显式结点,这些我们可以维护一下,记为\(\mathrm{link}(u)\)这样的。隐式结点的suffix link可以通过其第一个显式祖先的suffix link得到,也就是\(\mathrm{link}(xy)=\mathrm{link}(x)y\)这样的,我们从\(\mathrm{link}(x)\)出发找到\(y\)开头字符的出边
我们维护最短非重后缀对应的点,每次显式扩展最长重后缀的时候把最短非重后缀的suffix link指向它。
上面的没完全懂也没关系,接下来我们详细描述ukkonen算法 :
我们维护最长重后缀对应的结点\(cur\),用一个三元组\((u,c,p)\)表示,指它在\(u\)开头为\(c\)的出边上第\(p\)个位置(\(u\)是第\(0\)个这样的);维护最短非重后缀对应的结点\(last\)。然后由于它是后缀,可以发现\(c=s_{n-p+1}\),所以我们并不需要维护\(c\)。
现在插入字符\(s_{n+1}\),我们考虑当前我们认为的最长重后缀是否需要显式扩展。
如果它有一条\(s_{n+1}\)开头的出边,那么不需要显式扩展,这次插入结束。
否则,给它挂一个叶子,边上的串是\([n+1,n+1]\),这里如果它是隐式结点,需要先把它显式地建出来,也就是在这条边中间塞一个新点\(t\),令\(last:=t\)。
接下来我们需要\(\mathrm{link}(last):=cur,last:=cur,cur:=\mathrm{link}(cur)\)这样的,这里求\(\mathrm{link}(cur)\)得到的有可能是一个隐式结点。直到当前最长重后缀变成了空(或者某一轮不需要显式扩展了),插入结束。
结束之后,我们沿着当前\(cur\)的\(s_{n+1}\)开头的出边走一步,作为这一轮得到的新的\(cur\)。
为什么直接建立完整后缀树是困难的?注意到ukkonen里面用到了 一个后缀成为叶子之后就永远是叶子 的均摊,但是完整后缀树中,一个点成为显式结点之后,还可能变回隐式结点,可以构造一个串使得总共切换\(\Omega(n^2)\)次,我们就完蛋了。但是我并没有考虑或者查到怎么构造。
接下来我们考虑blumer的sam算法。
复读一下,sam每个点表示一个\(\mathrm{endpos}\)等价类。
考虑向右加入一个字符\(s_{n+1}\),\(\mathrm{endpos}\)等价类会有啥变化。首先显然只有新串的后缀的\(\mathrm{endpos}\)发生了变化,它们增加了一个\(n+1\)。因为每次增加的东西都不一样,我们知道\(\mathrm{endpos}\)等价类只会分裂不会合并。
可以注意到\(\mathrm{endpos}\)就是\(\mathrm{beginpos}\)反过来,也就是说我们把串翻转,\(\mathrm{endpos}\)等价类就变成了\(\mathrm{beginpos}\)等价类,而\(\mathrm{beginpos}\)等价类由完整st描述(每个\(\mathrm{beginpos}\)等价类是一个点和它的父边)。最小化是个很玄学的事情,而压缩比较直观,所以我们考虑完整st向前加字符会发生什么。发现这相当于插入了一个新的后缀,我们需要拿着这个新后缀在完整st上走到不匹配,然后把剩下的部分挂成一个叶子。所以我们知道最多加入两个点,一个点对应于走到不匹配的位置(可能本来就是一个显式结点),一个点对应于挂的叶子。
考虑这个不匹配的位置,就是最长的在原串中出现过的新串的前缀,把它反过来就是最长的在原串中出现过的新串的后缀,也就是新串的最长重后缀。那么原来和新串的最长重后缀在同一\(\mathrm{endpos}\)等价类中的串,长度\(\leq\)它的和它仍在同一个等价类,而\(>\)它的组成了另一个等价类,前者称为 短的 而后者称为 长的。
然后考虑转移边的变化。显然拆出来的那两个等价类的出边是和原来相同的,新叶子没有出边,所以我们考虑它们的入边。这两个点里面的串都是新串的后缀,所以只有原串的后缀有可能转移到它。考虑一个原串后缀组成的\(\mathrm{endpos}\)等价类。如果它之前没有转移\(s_{n+1}\),那么它现在应该转移到新叶子。如果它有转移\(s_{n+1}\)并且不指向被分裂的等价类,那么它的转移不变。如果它指向被分裂的等价类,那么由于它包含的都是原串后缀,它转移到的点应该是包含新串后缀的点,而这个点就是分裂出来的短的等价类。
然后为了枚举原串后缀,我们还是需要suffix link,这里suffix link从一个等价类指向它里面最短串的最长真后缀的等价类,对应到反串的完整st上就是父边。新叶子的suffix link显然指向最长重后缀所在的等价类,拆出来的两个等价类的suffix link由长的指向短的,而短的suffix link不变。
在具体实现的时候,我们先建出新叶子,然后从原串开始跳suffix link,找到所有不存在转移\(s_{n+1}\)的后缀等价类,然后第一个存在的,它的\(s_{n+1}\)转移就指向新串的最长重后缀所在的等价类,设为\(v\)。通过维护等价类中的最长串,我们可以判断转移到的点是否仅包含新串后缀,如果是则不需要进行分裂,否则按照上面的方法进行分裂,令\(v\)表示长的等价类,建立新点\(w\)表示短的等价类,然后继续跳suffix link,把本来指向\(v\)的转移改为指向\(w\)。
关于复杂度,可以注意到每次跳suffix link都意味着一个点从后缀变成了不是后缀,而每次插入只会增加最多两个点,所以复杂度是线性。
接下来我们考虑压缩sam。为了套用ukkonen算法,我们重新定义压缩sam为每个点代表一个\(=_L\)等价类中的最长串的\(\mathrm{endpos}\)等价类。
可以注意到st中所有叶子都变成了压缩sam中的同一个点,也就是说我们挂叶子的时候只需要连边而不需要建新点了,而这个叶子的父边仍然可以写成\([l,\infty]\)这样的来自动扩展。
所以我们考虑ukkonen建立的新点,以及\(\mathrm{endpos}\)等价类的变化会带来什么影响。可以感觉到我们会把一些新的显式结点合并成一个,并把一些原来的显式结点分裂开。感觉一下不可能把新的显式结点和原来的显式结点合并,因为这说明它们在同一\(\mathrm{endpos}\)等价类,应该已经被压缩了。只有当一个\(\mathrm{endpos}\)等价类都是隐式结点的时候,里面才会有隐式结点。
先考虑新的显式结点的合并。ukkonen中,除了挂上的叶子,剩下的新的显式结点都是变得不能唯一向右扩展的原串的后缀。
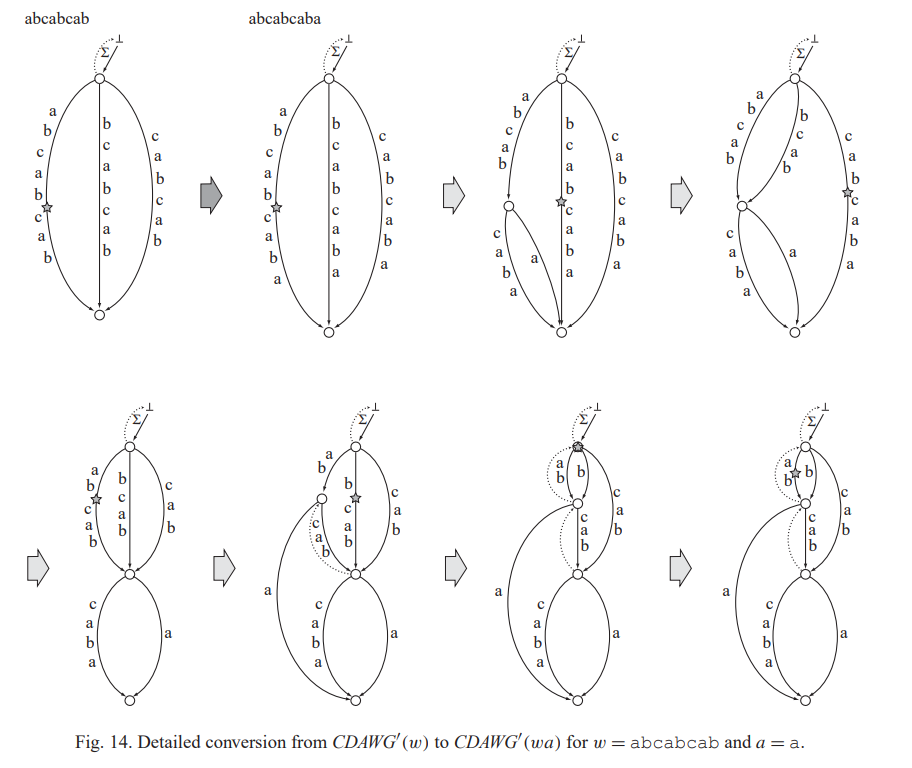
可以看一下论文中给出的这个例子。显然我们在跳suffix link的过程中,\(\mathrm{endpos}\)是单调增加的,所以经过的点分成若干段,每一段会被合并成一个。所以问题是我们要判断两个原串后缀的\(\mathrm{endpos}\)是否相同。
注意到显式结点之间\(\mathrm{endpos}\)必然不同,显式结点和隐式结点的\(\mathrm{endpos}\)也必然不同,只有隐式结点和隐式结点的\(\mathrm{endpos}\)可能相同,而隐式结点只有一条转移,所以只需要判断这一条转移是否指向同一个点。
接下来考虑原来的显式结点的分裂。blumer里面,我们会把最长重后缀所在的\(\mathrm{endpos}\)等价类分裂为长短两个,并新增一个等价类包含第一次出现的后缀。后者是叶子,所以只需要考虑前者。
ukkonen的一轮结束之后,\(cur\)会停在新的最长重后缀上,此时我们考虑它所在的等价类是否需要分裂。如果它是一个隐式结点,根据blumer那个按照\(\mathrm{maxlen}\)判断的方法,此时显然不需要分裂。如果它是一个显式结点,那么和blumer里面一样分裂即可。
具体实现的时候,我们用\((s,[l,r],t)\)表示一条边。先和ukkonen一样跳,一边跳一边判断这个点是否应该和上一个合并这样的,如果需要合并就直接连过去,如果不需要就新建一个。然后我们和blumer一样尝试进行分裂。
复杂度看起来就非常线性。
多串压缩sam
改成把多串ukkonen和多串blumer拼起来。不再赘述(
接下来我们考虑一个不是很板的板子题。
sdptt2022 r2 D4 C. string
给一个串,对它的每个前缀求完整压缩sam点数。\(n\leq 10^6,\Sigma=10\)。
简单做法是sam,lct。
考虑如何计算那些被缩进边里的点。考虑前缀完整st点数怎么做,发现这个比较好做,只需要维护长度\(\leq\)最长重后缀的后缀里面,有多少是隐式的即可。
但是前缀完整压缩sam点数要复杂一些,因为这些隐式后缀还可能合一合。不过这里爆力维护长度\(\leq\)最长重后缀的后缀里面,有多少是隐式的,并且其suffix link和它不在同一个\(\mathrm{endpos}\)等价类即可。由于一个后缀在变得不是后缀的时候必然被遍历到,所以我们完全可以维护这种东西。
感觉很对,哪天写一写/fn
Sasha and Swag Strings
给一个串,求它的完整st上每条边上的字符串的本质不同子串个数之和。\(n\leq 10^5\)。
发现完整st边上的串在完整csam边上仍然出现,所以我们只需要求完整csam边上的串的本质不同子串个数。可以注意到完整st相比完整csam,根据sam的结论我们知道完整csam边上的串总长是\(O(n)\),而完整st边上的串总长可达\(\Omega(n^2)\)。
那么接下来考虑怎么\(O(l)\)求一个串的本质不同子串个数。直接建sam即可。所以这个题需要你实现st,sam,压缩sam?
对称压缩sam
注意到正反串的完整压缩sam的点都是满足\(\mathrm{LRC}(t)=t\)的串,所以我们可以把它们拍成一个,此时它支持同时向两个方向加字符匹配子串。正反分别建压缩sam,然后直接hash就可以找到这个对应关系,复杂度期望线性。
模板 对称压缩sam
给一个串\(s\),维护一个串\(t\),支持向左/右加字符,查询\(t\)在\(s\)中任意一个出现位置,把\(t\)回退到某个版本。\(n,q\leq 10^5\)。
直接硬跳是不行的,因为我们不会处理隐式结点的转移。
考虑完整st上一个\(\mathrm{beginpos}\)等价类是一个点和它的父边,那么完整压缩sam上一个等价类是一个点和它的入边。于是我们跳的时候,维护\(t\)在当前这个点的最长串\(\mathrm{LRC}(t)\)中出现的位置,然后如果加一个字符离开了等价类,我们就去寻找一条对应字符开头的出边进行转移,否则只需要更新这个出现位置。然后这玩意很好可持久化。
接下来我们考虑一点恐怖题。
sdoi2022 子串统计
ptzsc18 Alice and Bob and A String