咕。
做了一个上古hdu多校博弈论题(09 contest3 E),然后发现自己爆了(
以下我们认为游戏都是两个人轮流进行,谁没法操作了就输了。
也许可以在 板子 找到板子。
定义
一个 博弈 描述一个博弈游戏的局面,它由左集合和右集合构成,每个集合包含若干个博弈,表示左方和右方(Alice和Bob)操作一步之后得到的局面。我们可以写作\(x=\{L\vert R\}\),这么写的时候一般把\(L,R\)的花括号省略掉。
博弈可能可以等于一个值或者能被逼近到一个值,这个值描述这个局面有多牛逼,也就是说这个值越大,局面对左玩家越有利。
一个博弈同时是一个 超现实数,当且仅当它左集合中的任何一个局面,都比右集合中的每一个局面要小。直观理解,就是说超现实数是越操作离死越近 的博弈,因为自己走总是比对方走更劣。
直接推论是,超现实数只能表示非常不平等的博弈,也就是两个人的决策没有交。
构造
首先我们有一个最简单的超现实数\(\{\vert\}\),它称为\(0\),显然是一个后手必胜的局面。
定义\(1=\{0\vert\},-1=\{\vert 0\}\)。刚才我们说过,超现实数描述的是一个局面有多牛逼,实际上这个数值的大小描述的是 左方可以通过这个博弈多活多少步。比如如果\(1\)这个博弈和别的博弈组合起来,那么左方可以在上面走一步变成\(0\),而右方只能去走别的博弈。刚才说过超现实数是越操作离死越近的博弈,于是\(1\)可以帮助左方赚一手,让右方离死更近一手,而\(-1\)相反。
我们可以构造一个\(\{1\vert\}\),它表示左方可以用一手把它变成\(1\),而右方什么都不能做。这个可以让左方赚两手,于是它可以称为\(2\)。
考虑\(\{0\vert 1\}\),这个的意思是右方可以用一手把它变成\(1\),并且不管右方是否进行这个操作,左方总是可以把它变成\(0\)。感觉上这个博弈对右方更有利,但是左方如果有兴趣也可以操作一次,也就是说这个数应该比\(0\)大而比\(1\)小。
考虑一个牛逼想法,类似于sb树,我们把这个称为\(\frac{1}{2}\)。类似地可以得到一棵二叉树 :
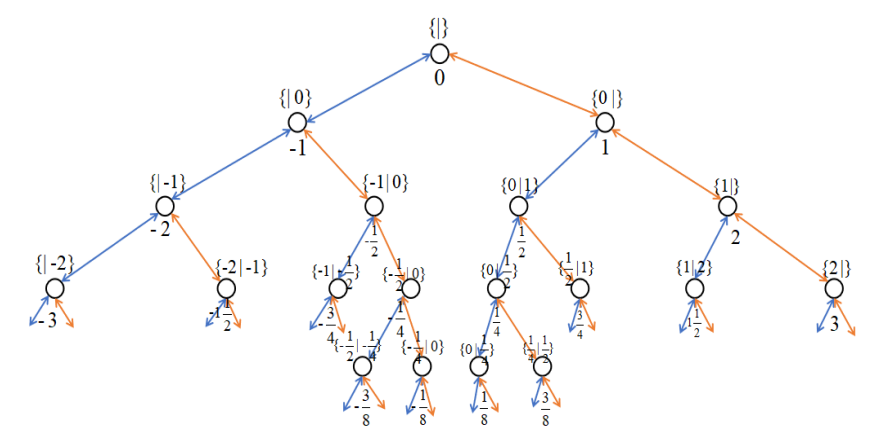
看起来可以在这棵树上对任意有理数进行逼近,但是如果分母不是\(2^k\)则永远不能达到。
简单性法则
显然一个博弈可以分别只保留左右集合中的最优博弈,于是每个博弈都可以简化成\(x=\{x_L\vert x_R\}\)。
简单性法则指出,如果存在\(z\)使得\(x_L<z<x_R\),那么\(x\)的值就是所有\(z\)中最简单的那一个。证明懒得写了(
那么什么是最简单的?超现实数的bst上只有所有形如\(\frac{a}{2^b}\)的数,我们定义最简单的是\(b\)最小的,也就是深度最小的,但是如果$b=0$它不一定是唯一的,如果\(x_L,x_R\)之间有至少一个整数,那么\(x\)的值就是这些整数中最接近\(0\)的,否则它是\(x_L,x_R\)之间分母最小的形如\(\frac{a}{2^b}\)数,这个数是唯一的,我们可以\(O(1)\)找到它。
注意这个主要适用于超现实数,因为只有超现实数才能用一个数代替,一般的博弈是难以用数代替的,从而难以直接用数值比较孰优孰劣。
显然的结论
\(>0\)当且仅当左方必胜,\(<0\)当且仅当右方必胜,\(=0\)当且仅当后手必胜。你问先手必胜?不要着急。
定义加法和加法逆
博弈的加法说的是两个博弈同时进行,每个人可以选择操作其中一个。有\(x_1=\{L_1\vert R_1\},x_2=\{L_2\vert R_2\},x_1+x_2=\{x_1+L_2,L_1+x_2\vert x_1+R_2,R_1+x_2\}\)。当然可以取最优的进行简化。
\(x\)的加法逆元说的是\(x^\prime+x=0\)的\(x^\prime\),这个东西看起来是\(x=\{L\vert R\},x^\prime=\{-R\vert -L\}\),含义是把两个人能做的操作反过来,一方只要模仿另一方就必然获胜,于是后手必胜。
Nimber,模糊博弈
在公平博弈(所以为什么不叫 非公平博弈,而是叫 不平等博弈?)中,每个博弈的左集合和右集合相同,胜负只有先手必胜和后手必胜。
sg定理说明了每个游戏(不只有nim,所有的公平博弈都是这样)都是一个值,多个游戏一起进行,得到的值是它们值的xor。
我们记\(\ast_n\),第\(n\)个nimber,表示和一个有\(n\)个石子的nim等价的游戏。两个nimber的和就是xor。
显然有\(\ast_0=0\),而\(\ast_{n>0}\)的值几乎是\(0\),因为在公平博弈中的胜负只差一个先后手,而对左右方没有什么区别。
但是这个值又不能是\(0\),因为\(0\)是后手必胜的。我们将先手必胜的博弈称为模糊博弈,用符号\(\parallel 0\)表示,这个符号写法是\parallel,读作模糊于。
\(\ast_1\)简写为\(\ast\)。
显然nimber的加法逆元是自己。
用这个可以构造\(\uparrow=\{0\vert\ast\},\downarrow=\{\ast\vert 0\}\),显然\(\uparrow=-\downarrow\)。可以理解一下它们的含义,\(\uparrow\)说的是一个特殊的石子,先手可以直接拿,但是后手必须进行一步 激活 之类的操作,而\(\downarrow\)相反。\(\uparrow\)是先手必胜的,\(\downarrow\)相反。同时容易验证它们的值非常接近\(0\),比任意超现实数的绝对值都要小。
现在我们有\(x,\ast_x,\uparrow\)三个东西(\(\downarrow=-\uparrow\)),它们可以线性表示出很多的博弈。
清华集训2017 福若格斯
游戏的内容是,有五个格子,一开始左边有两个朝右的青蛙,右边有两个朝左的青蛙,中间是空的。左方可以操作往右的青蛙,如果这个青蛙右边是空格,可以走过去;如果右边是往左的青蛙,再右边是空格,可以跳过去;右方是对称的。不能进行就输了。
只有23个状态,可以搜出状态之间的转移(或者手玩?),然后推出它们对应的博弈,最后每个博弈都可以用\(\frac{a}{2}+b\ast+c\uparrow\)表示,其中\(b\in\{0,1\},c\in\{0,1,-1\}\)。这个转移很简单,究其原因是只有一个分支。
热度
平移原理断言,
原子量
如果若干个博弈的和非常接近\(0\),我们如何判断这个和的正负?