joi题选做

写的还是比较拉，会在新开的 oi题选做里面把这些再补一遍。

本来是几个loj上的选做计划，然后只开了joi一个坑，后来发现loj的joi并不全，于是去atc上找了，于是就改名成刷穿joi了（

怎么感觉joi经常被到处搬（

发现dwt已经把这些刷穿了（

joi大概是，final相当于noi，sc相当于ctt cts，open相当于wc这样的。

https://www.ioi-jp.org/problem_archive.php

可以看到全部官方题解。joi open的题解往下翻，可以看到有一个joi open的列表，然后你就找到了。但是可能需要梯子(，也可能不需要，跟github一样玄学)。

loj2332~2336 joi 2017 final

A. 焚风现象

注意到每次修改只会影响区间两边的间隔，于是用BiT支持区间加单点查询即可。

更简单的做法是维护差分，就变成单点修改单点查询了。

B. 准高速电车

考虑我们要想到一个车站，必然是先坐快车，再换准快车，再换慢车。也就是说，每个车站的距离，是它坐慢车到前面第一个准快车站的距离，加上这个准快车站到前面第一个快车站的距离，加上这个快车站到\(1\)的距离。

首先可以按照快车站划分成若干段。显然是往靠前的段里，尽可能往后塞准快车站是最优的。注意到每一段都是塞的越多，再塞就越没用，于是这个是上凸的，于是我们可以闵和一下，实际上它就是每次选取再塞一个答案增加最多的一段。

C. JOIOI王国

这个划分方式就是画一个单调的斜线，当然往哪个方向单调不一定，不妨假设从左上往右下斜。

注意到这是两个东西的极差，而这两个东西并起来是所有东西，也就是说要么答案是全局极差，要么全局\(\max\)和全局\(\min\)分处两个省。

于是我们钦点包含全局\(\max\)的是A省，包含全局\(\min\)的是B省，A省在左边而B省在右边。枚举A的\(\min\)，最小化B的\(\max\)。

我们先把所有可以包含在A省的位置(也就是介于全局\(\max\)和我们枚举的\(\min\)之间的)标记成1，别的标记成0，然后目标就是在只能拿1的情况下，最小化没拿到的1的\(\max\)。

你发现最小化\(\max\)这件事，等价于尽可能多拿，让外面剩下的少一些。然后考虑它的结构，每一行一定是尽可能多选，除非后面会不满足单调。我们维护每行的极长前缀1长度，那么每个位置实际上选的长度就是这个的后缀\(\min\)。怎么维护这个东西的话，可以从大到小枚举那个\(\min\)，这样每个位置都只会增加，直接爆力更新复杂度就是对的。

现在问题是怎么维护每个位置实际上被选了多少。注意到这个东西也是只增不减，于是我们还是可以强行更新，但是怎么强行更新?一个位置增加了，如果它是后缀\(\min\)，那么它到它前面那一个后缀\(\min\)都会提高一些，于是强行再对这一段扫一遍，更新一下并维护新的后缀\(\min\)就好了。除去排序，总复杂度\(O(nm)\)。

看一眼题解，另一个简单做法是二分答案，然后每个格子要么只能分到A省，要么只能分到B省，要么都可以，于是我们尽可能把只能分到A省的搞定，剩下的分到B省即可。但是我觉得我的做法也很对啊?

呃它确实是对的，但是不知道为什么它跑的就是很慢，可以在https://loj.ac/s/1325779看到。懒得实现结构体基排了。

D. 足球

先假设\(a<c\)，不然没的玩了。

注意到\(h,w\)小的可怜。

考虑这个有没有什么性质。每次球的移动一定是向着目标的方向吗?

好像不一定。考虑如果带球的代价非常大，传球的代价则很小，我们会希望尽可能传球，而可能会有一条曲折的人链恰好可以传过去这样的。

呃倒是有一个显然的性质，一个人不可能两次接球，即使他中间做了跑动。因为他完全可以在第一次接球的时候就带着球跑到第二次传球的地方。

于是考虑球的运动过程中，我们难以描述的就是一个人跑过来接了这个球，然后带了一段之后把它传出去了。现在我们知道不带球的跑动只会发生在接球的时候，并且一个人两次接球一定不优，于是这个跑过来接球的人必然是离球的落点最近的人。所以我们直接建图，用路径表示球的运动过程。

带球的代价是\(c\)，于是我们给相邻的点连\(c\)。

从\((i,j)\)传到\((i,k)\)的代价是\(a\vert j-k\vert+b\)再加上离\((i,k)\)最近的人跑到\(k\)的代价，于是我们给每行再建一排点表示这行上空的球，每列也是，传球的时候进入上空花费\(b\)，每一步花费\(a\)，而落地的时候花费最近的人跑过来接球的代价。最近的人可以直接bfs掉，而最短路的部分边权只有三种，可以用三个队列代替堆，复杂度是\(O(hw)\)。

诶这个东西好像有点小问题。我们刚才说一个人不会接球两次，但是这里对于一个人接球两次的路径，算的并不是他接了第一个球再跑过去接第二个球的代价，而是他传出第一个球就无代价瞬移回到初始位置，再跑去接第二个球的代价。所以这还对吗/yiw

先写一发，你发现过了。

想一想你发现这居然还是对的。我们只需要说明有一个合法方案比这个算假了的优。考虑一个人接球的时候，一定是有一个人踢给他，于是让这个人往他最后一次出球的地方跑一段就好了，画画图你发现这是对的。这么简单的问题我想了一下午?

E. 绳

看题面感觉啥想法也没有。为什么绳长最后是\(2\)而不是\(1\)?

你发现如果是\(1\)，我们只需要把所有的都染成同一个颜色，此时就都染成一开始最多的那个颜色就行了。所以就没有难度了（

如果是\(2\)，我们可以先枚举一手两段都是啥颜色，分别记为10。然后考虑一开始每一段是什么颜色。什么样的颜色序列是可以拧成两段的?

考虑如果仅仅是要判定的话，我们可以考虑最左边的那个东西，假设它是1，那么我们往右找到最近的1，然后把它和这个1折起来。如果这中间是奇数个0，你发现我们折不起来，这样的话到最后这两个1也总是折不起来，于是必然不行。所以除了开头结尾，每一段长度必须是偶数，根据前面的构造这个必然可以折起来。我们可以先枚举一波开头，这样结尾的长度奇偶性也确定了，于是剩下的每一段都是偶数。

然后你发现，我们不光一定可以折起来，并且一定可以只把左边折到右边，除非最后只剩下一个什么和一串连续的另一个，比如10000000这样的。我们枚举这个一个什么(例子中就是1)的位置，然后右边全是0，左边强力dp，复杂度是\(O(nm^2)\)。飞了?

考虑如何优化。这个颜色有没有什么性质?显然的事情是，选了一个颜色1，确定了一个方案之后，另一个颜色0一定是不是1的所有位置上，初始颜色的众数。方案要dp听起来也很离谱，能不能贪?

能不能把第一个枚举也加入dp的状态，让转移变成二维数据结构问题?你发现感觉上这个很困难，所以就没救了。还是考虑先确定一个颜色或者贪心构造方案吧。

王卷王之言可谓切中了肯綮。注意到我们为了把一段搞成偶数长度，把一个1变成0和把一个0变成1是一样的，但是把0变成1一定有代价，而把1变成0可能会影响众数从而减少代价，于是我们钦点只会把1变成0。把所有数相邻两个一组，于是00一定不变，11一定不变，01变成00。

还有一些牛逼性质没有用来着!所有颜色的出现次数和是\(n\)，所以考虑能不能让一个颜色的计算代价是\(O(c)\)，当然\(c\)是出现次数。把连续的00放在一起处理即可。剩下的问题是求一些众数，注意到如果你删的颜色不是全局众数，那么众数还是全局众数，否则可以爆力重新求。

loj2342~2346 joi 2016 final

A. 橙子装箱

强行dp，用st表维护min/max。

B. 集邮比赛2

那个1在loj也有，是joisc 2014 邮戳拉力赛。

看起来意思是，加一个字符，最大化子序列JOI的个数。

我们枚举放在哪，考虑所有经过它的子序列。如果这是一个J，我们需要知道后面的OI的个数；如果是O，我们需要知道前面的J和后面的I的个数。总之就是可以算，所以就算就行了。

C. 铁路票价

动态图最短路/jy

先搞一个最短路DAG，沿着最短路DAG走得到的都是最短路，于是剩下的问题相当于删边，查\(1\)能到多少点。

这个咋做?倒过来变成加边即可。实际上一开始就倒过来也是可以的。

D. 领地

计算几何/fn

注意这个领地个数并不是围成的区域面积，因为如果我走了一个大圈，里面并不是我的领地。

爆力怎么做?考虑每走一轮的偏移量至少应该是\(1\)，否则我直接算一轮就好了。于是我们可以考虑算前\(n+2\)轮，第\(n+3\)轮所产生的贡献和\(n+2\)轮应该是相同的，因为前面对这两轮的影响是相同的。为什么\(+2\)?因为觉得不加不太对，所以就随机加了一个数。

现在问题是折线长度1e5，我们要算1e5轮，以及算第1e5轮新增了多少。第二个可以归约到第一个。

考虑怎么算这个前面对后面的影响。我们考虑某一轮，把它的起点平移到\((0,0)\)，然后考虑每个方格，计算前面至少需要已经有多少轮，才能让这个方格恰好在这一轮被占领，也就是这个方格的一个角在这一轮第一次被走到，另外三个在这一轮或者这一轮之前被走到。算出这个的话就可以随手统计答案了。

考虑这个问题相当于查询一个点在某种平移下，经过最少的次数平移到另一个点，也就是查询一条斜线最下面或者最上面的点，而斜线的斜率是固定的。用hash table维护每个点所在的斜线截距(或者你可以排序离散化?)，扫描线扫过去即可，复杂度\(O(n)\)。

E. 断层

感觉难度在于理解题意（

大概说的是，地层有无穷层，每层被划分成\(n\)个长为\(1\)的段，每次会有一个断层来斜着平移这些段，问你平移完了地面上每一段原来在哪一层。

平移像是均摊线段树之类的，但是这玩意看起来没有任何均摊性质……

考虑直接枚举每一段，看它是哪里来的。你发现它可能经历过若干次平移，每次平移会递归到另一段，于是我们有了一个\(O(nq)\)的做法。

考虑\(q\)个断层会把所有的东西分成\(q^2\)个区域，每个区域内的变换是相同的。于是进行分块，复杂度\(O(n\sqrt{q})\)，离线下来一起处理每一块的话，空间是线性的，感觉上应该很快。

能不能更优呢?查一手题解，发现有1\(\log\)做法。

注意到分块里面我们是倒着强行处理这些区域，于是考虑我们直接倒着做，然后就变成了平面上有一些点，支持半平面平移，最后查询每个点的位置。诶这个问题是不是随手就做掉了，为什么一开始没想到这个……

考虑为什么随手就做掉了。两种半平面分别是\(y+x\geq k,y-x\geq k\)，操作是\((x:=x+k,y:=y-k),(x:=x-k,y:=y-k)\)。注意到不管怎么操作，两个点的\(y+x,y-x\)相对顺序总是不变，因为左边的会越来越往左，而右边的越来越往右。同时第一个操作不影响第一个不等式，第二个操作不影响第二个不等式，于是直接两个线段树维护一下，在做第一类平移的时候，去第二类的线段树上二分出来平移的是哪一段即可。复杂度\(O(n\log n)\)。

技不如人啊/ll

loj2347~2351 joi 2018 final

A. 寒冬暖炉

怎么想都像是有凸性，直接wqs二分。写一发过了（

简单做法是，我们直接从小到大取这些间隔。离谱（

B. 美术展览

按尺寸排序之后，把价值和差分掉。

C. 团子制作

问题出在，一个团子只能贡献给一串。

考虑先求出所有可能的串，然后考虑它们有什么性质。注意到这些串，横着的之间不会相互影响，竖着的也不会相互影响，并且只有在同一条斜线上的才会相互影响。于是我们只需要每条斜线状压dp一下就好了。但是这只是论述了必然能做。

继续考虑它的结构，显然这个问题是一个最大独立集。我们为每一串建一个点，那么因为只有横竖之间才有影响，这个图就是二分图，可以用网络流解决。但是这个比状压dp要劣（

考虑一条斜线，这上面的所有串在这个二分图上连起来的形态看起来很有趣。实际上这个东西直接做还是状压dp?但是画一画这个图会让你立刻理解到状压dp应该如何写（

查了一下，发现正解真的是这个/jy

D. 月票购买

首先两条路径的交必然是一个区间，也就是说我们选择的\(u\)到\(v\)的路径上置\(0\)的一定是连续的一段。

考虑我们枚举交的那一段的两个端点，然后判断这一段能不能在\(s\)到\(t\)的最短路上。这个非常爆力，但是至少它是多项式复杂度。

判断能不能在\(s\)到\(t\)的最短路上这件事，爆力就是Floyd，那么有没有什么牛逼的方法?考虑\(s\)到\(t\)的最短路DAG(也就是每条无向边拆成两条有向边，如果一条边在某条\(s\)到\(t\)的最短路上，那么它就在\(s\)到\(t\)的最短路DAG上)，我们可以跑出来每个点可以到哪些点，而这些点对就可以，别的就不行。这是最短路DAG的性质，也就是一条路是最短路，当且仅当它在最短路DAG上。

也就是说接下来我们要选择两个点\(x,y\)，满足最短路DAG上\(x\)可以到\(y\)，并且\(d(u,x)+d(y,v)\)最小。啊当然我们需要把\(x,y\)反过来再跑一遍。

这个怎么做?我们直接在最短路DAG上跑拓扑排序。做完了。

E. 毒蛇越狱

考虑这个东西能否用类似于法嘛塔的东西办了。感觉上不行，因为\(3^{20}\)足足有3e9，而法嘛塔总要把这些东西都塞进状态。

考虑能否强行逐位考虑?问题转化成维护一个集合，一开始是固定的1e6个数，每次删掉某一位是某个值的所有数，问最后所有数的和。这个听起来没法做。

吗?注意我们可以离线。考虑这相当于在一个\(3^{20}\)个状态的树上走，我们走过了的地方就不需要再走了，可以直接拿来用，这个可以直接在状态上一边走一边同时划分所有的查询来解决。考虑所有的查询最多可以经过多少个结点?显然是\(2^{20}\times 20\)的级别。考虑了一下，感觉上这个东西再怎么分析不会低于\(O(2^{(1+\epsilon)n})\)，于是还是别想了，不过要是在场上就先rush一发再说（

考虑能否折半之类的?这让我想起一个牛逼题，是21年二轮省集D6T2，然而这两个还是不是很像。我们考虑进行某种分治。

如果查询中的?超过一半，那么我们就找到所有不是?的位置，同时对于原序列中每个数，枚举它保留一些位置，把剩下的位置换成?的方案，这样的方案一共有\(\binom{20}{10}=184576\)种。
如果查询中的?不超过一半，我们枚举一个把这些?换成01的方式，同时对于原序列中每个数，枚举它把一些位置换成?的方案。

总复杂度\(O(2^n\binom{n}{n/2})\)。根据斯特林近似我们知道这玩意大概是\(O(n^{n/2}e^{-n/2}2^n)\)，它比\(O(3^n)\)要劣，并且实际表现也是这样，它的算量大概是1e11。

我们要做什么样的预处理，才能让回答询问的速度变得很快呢?

考虑另一种折半的方向，我们注意到\(3^{15}\)大约是1e7，于是考虑法嘛塔预处理前15位的结果(也就是忽略后5位)，它的算量是1e8级别，然后考虑如何加入剩下的5位。

我们需要新增一些限制，这样会有一些东西没掉。考虑是哪些东西，你发现回到了第一个想法/ll

完全不会了。考虑一个牛逼做法，我们强行把?当成1，然后跑子集前缀和。这样会有一些应该是1的位置被考虑成0，于是我们就完蛋了。考虑一个没办法的办法(但是这里是绝妙的办法)，我们进行容斥，这样如果查询有\(c\)个1，复杂度就是\(2^c\)。于是我们找到01中较少的，一开始分别跑子集前缀和和子集后缀和，复杂度是\(O(2^nn+q2^{n/2})\)，可以获得75pts。

如何继续优化?考虑继续分治，如果?很少，我们直接搞?，复杂度变为\(O(2^nn+q2^{n/3})\)，可以通过。

我只能说太强了。这题强到没救。

loj2413~2414 joi open 2017

没有A。

B. 推土机

考虑我们转转转，然后求一个最大子段和。这个转转转中，点之间的顺序只会改变\(n^2\)次，于是我们爆力搞出这些变化，每次是交换相邻的两个，线段树维护最大子段和即可。总复杂度\(O(n^2\log n)\)。

C. 高尔夫

球必然会撞在一条线或者它的延长线上，或者和终点在同一直线再停下。每条线尽可能往两边延长，然后每条线建一个点，然后每条线连相交的线，这个可以线段树优化建图。

loj2724~2728 joi 2015 final

A. 铁路旅行

看了一眼感觉很困难，再看一眼发现是序列（

差分-前缀和一下算出每条铁路被经过多少次，然后看它是买票便宜还是买卡便宜就好了。

B. 分蛋糕2

直接复制一倍区间dp。

C. JOI公园

先从\(1\)跑dij，然后就可以知道打地道的范围要多大，一条边才会消失，做一个后缀加即可。然而这个范围最大可以达到1e10，我们需要对最短路离散化一下。

D. 舞会

草，为什么我会做到这个题，这是我初二的时候在bct见过的题，当时觉得非常牛逼（

每次留下中位数。

二分答案转01，然后我们让每个人表示，至少需要放多少个熟练度是1的人，才能让这个人的熟练度是1，最后看1的总数够不够即可。

E. 城墙

4e3/jy

直接做的复杂度是\(O(n^3)\)，这会飞掉。你说10s?sorry，肯定跑不过。

不过看起来复杂度是\(O(n^2\log n)\)或者\(O(n^{2.5})\)之类的东西。

考虑几种直接做的做法。本质上所有的爆力都是枚举了三条边，但是这里我们显然只能枚举两条，于是需要考虑枚举哪两条。

我们先枚举左边和右边，然后考虑这个正方形上下的位置。首先可以把左右边上有障碍的情况都删掉，这个怎么想都不超过4e8，随便跑了。问题变成两条横线上都不能有障碍的方案数。

讲道理，一条都不好做。诶一条好像是好做的，我们只需要从每个点出发强行往右延申就好了。

那么现在设一个格子延申的长度是\(f(i,j)\)，当前枚举的边长是\(l\)，我们就是要求左边\(x\)上有多少对\(i,j\)满足\(f(x,i)\geq l,f(x,j)\geq l\)之类的东西，可能还有一些\(\pm 1\)不过那不重要。

这玩意看起来像是法法塔吗?想了想你发现不行。fuck!换一个。

注意到，如果先枚举左边和下边，也就是先枚举左下角，那么剩下的两条边会形成了一个拐角的形状，而我们可以让它只剩下右上角一个变量。

我们让每个点强行往左、往下延申，看最多延伸到哪里，这个记为\(f\)。然后枚举左下角的时候，计算往右、往上最多延伸到哪里。那么可以画个图解释一下 :

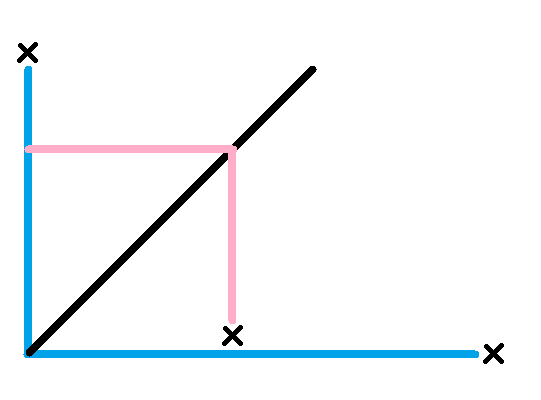
然后你发现我们要求右上角那个点的\(f\)要比它到左下角的距离更大，这个大概是什么\(f(x+k,y+k)\geq k\)之类的，移一项就变成\(f(x+k,y+k)-\frac{1}{2}(x+y+2k)\geq-\frac{1}{2}(x+y)\)之类的(当然是固定了斜线所以可以随便移项)，然后就变成在一条斜线的区间上查询比某个数大的数的个数，这完全是二维数点，扫描线BiT即可。

这个题告诉我们两个道理，一个是只要你能枚举所有的扫描线方向，肯定可以做出来；另一个是能快速减少变量数量的扫描线方向直觉上看起来会更优。

loj2741~2743 joi open 2016

A. JOIRIS

所有的块都是一样的，这就看起来比较离谱。

简单想法是，我们直接模拟。考虑找到最左边的最低的位置，然后它必须塞上一个什么东西，那么我们就给它塞点什么东西上去。如果能放横着的那就放横着的，否则放竖着的。

你发现这个不行，它过不了第一个样例。离谱¿

不会了。看题解。但是这个题解好难找（

另外第一个样例也告诉我们，消除是有用的，我们不一定总是从上往下消。

先考虑点性质。把列按膜\(k\)分成若干等价类，每个等价类高度都加起来，那么横着放会让所有等价类\(+1\)，竖着放让一个等价类\(+k\)。最后前\(n\bmod{k}\)个等价类相同，后面\(k-n\bmod{k}\)个等价类相同，所以一开始也必须满足这两个性质。

还有啥性质?不知道。想不出来了。

那么我们强行构造。

首先考虑，我们塞竖着的不会改变有没有解。所以我们可以强行塞竖着的，把它变成单增的。

接下来，我们尽可能塞横着的(即使塞了会不满足单调)，从而把\(k\)列和右边的全部推平到同一高度。然后尽可能塞竖着的，从而把\(k\)列和右边的全部清空。现在只剩下左边\(k-1\)列。

考虑现在前\(n\bmod{k}\)列膜\(k\)是一样的，接下来的\(k-n\bmod{k}\)列膜\(k\)是一样的。注意到\(k\)列清空了，所以\(n\bmod{k}+1\)到\(k-1\)列实际上也全是\(0\)。我们把前面\(n\bmod{k}\)列补齐，然后不停往右边放横着的，就可以清空了。

这个题的做法其实很直接，只是有些时候我不敢想这种强行的做法，其核心就是不断尝试简化问题。

B. 销售基因链

简单题。有一个线性做法，可以在 Sxy_Limit的博客 https://www.cnblogs.com/Sxy_Limit/p/12930980.html 看到。

C. 摩天大楼

好像是经典题，但是我没做过（

复杂度像是\(n^2v\)或者\(n^3+v^2\)之类的。

扫序列毫无前途，我们扫值域。考虑最大的那个数，它的贡献一定是正的。

考虑次大的数，它的贡献几乎是正的，除非它和最大的挨着，那么它会贡献一次负的。第三大的数，如果挨着最大的和次大中的两个，那么会贡献两次负的，挨着一个则贡献一次负的，不挨着则都贡献正的。

我们怎么描述和更大的数挨着这种事情呢?我们可以在旁边两个位置上留一手接头，表示放在这两个位置会贡献一次负的，如果一个位置被标记两次那就是贡献两次负的。不妨把它们称作1接头和2接头。

考虑我们怎么才能记录两类接头的数量。你发现不能，因为位置会影响数量的变化。遇到了僵局。

不要考虑数量的变化，我们钦点这些接头!也就是说放进一个数去，直接钦点它左边和右边的接头在被消除的时候是1还是2，如果是2那就需要留一手，让后面一个数来把它变成2，留一手这类接头我们称为1.5。接下来我们记录有多少个1/1.5/2接头即可。然而还是有问题，我们如果要把左右两个1都变成2，可能实际上没有位置可以做这件事，这就很难受。

这个思路完全失败了。还有什么?

可以考虑插入而不是摆放。

此时扫值域的优势完全体现了出来，我们插入一个数，两边的数都比它大，设这三个数分别是\(a,x,b\)，那么贡献会增加\(2(\min(a,b)-x)\)。考虑我们把这个拆开，每次插入之后直接把\(2(\min(a,x)+\min(x,b))=4x\)扔进总和，\(-2x\)在插入的时候加进去，这样。同时维护所有空位多加了的东西，也就是所有间隔的\(\min(a,b)\)之和，最后减去即可。

你发现这个多加了的东西没法维护，因为我们插入的时候，需要知道这个间隔原来的\(\min(a,b)\)，这就完蛋了。

怎么才能把这个去掉?考虑我们在插入的时候，钦点新产生的空位以后还会不会被插入，也就是多记一个还有多少没被钦点没了的空位，转移的时候我们只往这种空位里面放，最后所有的空位都被钦点了，那就对了。

设\(dp(i,j,0/1/2,k)\)表示考虑前\(i\)个数，有\(j\)个中间的空位没被钦点，\(0/1/2\)个边上的空位没被钦点，当前总和是\(k\)。转移就是考虑插到中间还是边上，然后新产生的空位是否要钦点。写一发你发现对了，OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO!但是这个的状态数是\(O(n^3v)\)，转移是\(O(1)\)，过不了。

考虑对第三维优化掉一个\(n\)，我们需要某种方法使得统计和的时候不会有负的，这样就可以利用\(L\leq 1000\)了。考虑我们这个东西实际上是一个线头dp，我们留接头的时候，可以一边扫一边加上这一步的长度乘上线头的个数，而不是进行差分。这就做完了。如果要直观描述这一做法的话，就是把这个排列想象成折线，然后从上往下扫，记录扫描线上方的长度和接头的个数。

\(O(n^3v)\)的做法可以在 https://loj.ac/s/1328392 看到，\(O(n^2v)\)可以在 https://loj.ac/s/1328415 看到。

这个题告诉我们，只要你能枚举出所有的扫描线方向和所有的转移结构，什么题都可以做出来，所以做数数题一定要充分自信，敢于硬想(不包括带项式题，那个不可能做出来的)。另外就是，我们可以钦点产生的接头类型，从而使用线头dp来rush。

loj2756~2760 joi 2014 final

A. JOI徽章

模拟。

B. IOI馒头

背包。

C. 年轮蛋糕

最小值最大，先二分再说。诶这种\(n^2\)个数二分的题是否有什么把\(\log v\)变成\(\log n\)的技术啊（

然后我们要让每一块大小都比二分的数要大。这个怎么做?我们先枚举第一刀切在哪，于是贪心地，接下来每一刀都希望切的尽可能近一点，于是我们双指针扫一遍求出来最近切到哪，然后直接看有没有一个位置可以切一圈就好了。

D. 飞天鼠

看起来这是一个最短路问题。直接做，状态数是\(nv\)级别的，这就很不好，于是我们希望缩减状态数。

首先一个显然的结论是，如果确定了一条路线，那么我们除非迫不得已，否则不会爬树。也就是说，我们会一直下降直到不能继续下降，然后就相当于在这个点从\(0\)开始了。

于是我们把这个过程分成了三段，第一段求第一棵树只使用下降到达每棵树的最小时间(此时高度必然最大)，第二段求每棵树用恰好的升高走到相邻的一棵树，把高度变成\(0\)的最小时间，第三段求每棵树的高度\(0\)处走到最后一棵树的最小时间。做完了。

E. 裁剪线

为什么joi这么喜欢计算几何（

这个问题是求平面被划分成了多少区域。这让我们想起什么?欧拉公式。扫描线线段树即可。

另一个想法是扫描线的过程中维护连通性。我们从左往右扫，如果扫到了一个横的起点那就进行分裂，横线的终点就进行合并，扫到竖线那就切断一个区间和后面的联系。总之就是很复杂。

loj2761~2765 joi 2013 final

A. 彩灯

考虑枚举是奇数位黑色还是偶数位黑色，然后问题变得显然了。

B. 搭乘IOI火车

题意是，两个01序列，分别找一个区间，使得它们可以归并成0101010101010101这样的，最大化归并出来的长度。

这玩意居然让我一时不会做了（

考虑dp，设\(dp(i,j,0/1)\)表示第一个左端点选\(i\)，第二个选\(j\)，第一个字符是\(0/1\)，最多能搞出多长，转移显然。

C. 现代豪宅

考虑建两层图，分别表示按了奇数次和偶数次之后的情况，只往图里加特殊点，每个点只会贡献两条边，于是总边数就是对的。

D. JOIOI塔

实际上是说能找出多少个不交的JOI或者IOI子序列。

考虑网络流，众所周知hlpp可以跑1e6!

想了想你发现不能网络流（

你发现问题出在，我们不知道一个I应该贡献给第一个字母还是第三个字母。

二分答案，这样我们尽可能在右边凑出足够的OI，然后就不再需要OI了。

线性做法也很简单。我们考虑一定是一个前缀的I贡献在第一个位置，剩下的那个后缀的I贡献在第二个位置，于是我们对每个前缀尽可能匹配JO,IO,J,I这样的，对后缀匹配JOI,OI,I，然后枚举中间的分段点来合并即可。代码可以在 https://loj.ac/s/1328750 看到。有别的牛逼线性老哥跑的比我还快?

E. 冒泡排序

惊悚题目名（

同时是loj round #6 C. 花火。

然而是关于逆序对数的问题。做一次交换最小化逆序对数的话，考虑如果我们交换\(a_i,a_j(i<j,a_i>a_j)\)，会发生什么变化。呃为什么\(a_i>a_j\)?交换顺序对显然是不优的啊（

对于不包含\(i,j\)中任何一个的对，显然没有变化。对于\(i\)前面或者\(j\)后面的某个\(k\)，跟\(i,j\)中的某一个组成的对，也没有变化。

那么也就是只有区间\([i+1,j-1]\)中的某一个东西和\(i,j\)中的某一个组成的对会产生影响了。如果一个位置\(k\)满足\(i<k<j\)且\(a_i>a_k>a_j\)，交换\(i,j\)会让包含\(k\)的逆序对减少两对。如果\(a_i>a_k=a_j\)或者\(a_i=a_k>a_j\)，那么只会减少一对。

\(i<k<j\)且\(a_i>a_k>a_j\)，这个描述了一个矩形\([i+1,j-1]\times[a_j+1,a_i-1]\)。于是我们现在可以\(n^2\)用二维前缀和做这个。

考虑我们应该怎么选取扫描线方向。显然的想法是扫\(k\)，但是扫了\(k\)之后变成了四维的，这就很难受。

差分。这个相当于是\([1,j-1]\times[1,a_i-1]-[1,i]\times[1,a_i-1]-[1,j-1]\times[1,a_j]+[1,i]\times[1,a_j]\)。现在每个问题是四个二维的和，于是我们就让每个贡献贡献给这四个问题即可。做完了。

吗?这个还是四维的/cy

所以怎么办呢，看起来我们必须找一点性质。考虑什么样的\(i\)一定是不优的，你发现如果有一个\(i^\prime\)使得\(i^\prime<i,a_{i^\prime}>a_i\)，那么\(i^\prime\)比\(i\)更优。所以说我们单调栈筛出所有前缀\(\max\)，它们是所有可能的\(i\)，而显然后缀\(\min\)是可能的\(j\)。

考虑单调性有啥用。你发现以前一个\(k\)贡献的是所有\(i<k<j\)且\(a_i>a_k>a_j\)的，现在\(i\)们和\(j\)们的\(a\)都单增了，所以\(a_i>a_k\)的\(i\)是一个后缀，\(a_k>a_j\)的\(j\)是一个前缀，于是每个\(k\)贡献一段区间，这就变成二维的了。扫描线线段树即可，复杂度是\(O(n\log n)\)。

一个更见鬼的方法是决策单调性分治。从小到大枚举\(i\)，对应的最优的\(j\)是决策单调的，于是分治即可。需要数据结构支持数点，所以会多一个\(\log\)。

但是为什么它是决策单调的呢?我不知道，不过这样的结论猜起来也不困难，决策单调已经是应该枚举的性质了。

loj3010~3014 joi 2019 final

A. 勇者比太郎

看起来就是一个拐。考虑我们扫什么，你发现不管扫什么都可以，当然简单做法还是枚举\(i,j\)，预处理\(k,l\)(\(k,l\)是独立的)。

B. 这看起来至少是一个二维lis。

呃等等，lis个锤子，这是无序的/jy，我对着lis想半天（

考虑直接贪，同时从大到小扫框和画，找到可以放进来的画中美观度最大的即可。

C. 有趣的家庭菜园3

只有400/jy

交换相邻/jy

问题是求重排成没有相邻的之后，最小的逆序对数。显然我们重排之后，对于所有的R，一定是按原序列中的顺序排的，GY是一样的。

考虑直接dp最后的序列。我们记录现在用了多少RGY，然后要计算逆序对数的话，也就是每在最后插入一个，需要知道前面有多少比它大。设\(dp(i,j,k,0/1/2)\)表示放了\(i\)个，其中RGY分别\(j,k,i-j-k\)个，最后一个是R/G/Y的方案数，转移看这个放了啥。假设放R，那么可以随便求出这个R在原序列中的哪里，这个设为\(x\)，则逆序对数要加上前面比\(x\)靠后的数量，也就是要支持\(x\)到第\(k\)个G之间有多少G这样的问题之类的，前缀和随便做就行了。

D. 硬币收藏

问题是找到一个\((1\leq x\leq n,1\leq y\leq 2)\)的排列\((a_i,b_i)\)，最小化\(\sum\vert a_i-x_i\vert+\sum\vert b_i-y_i\vert\)这样的。

注意到每一个硬币总要进入\([1,n]\times [1,2]\)这个矩形，所以可以先把所有点移动到这个矩形中离它最近的点。因为是矩形，这样做一定不劣。

然后问题是我们需要把这些硬币移动到正确的位置去。讲道理这是不是很经典（

但是我写了两发假贪心都挂了/fn

考虑一个真贪心，我们从左往右扫，维护两行各有多少多余的棋子，这个可以是负的，表示有多出来的空位。然后讨论一下就行了。

这个题大概是告诉我们，处理这种移来移去的问题，可以把空位留到后面进行决策，这可能会把问题变得显然。

但是是不是有无脑强力做法呢?不知道。

E. 独特的城市

看起来这个说的是，对于每个\(u\)，把所有点到\(u\)的距离拿出来，对独特的点求一个颜色数。

草，怎么是树啊（

考虑这个独特的点的集合说的是什么。我们以\(u\)为根把树拎起来，那么如果一个深度只有一个点，它就是独特的，这是显然的。

先考虑颜色互不相同怎么做。

考虑分治?感觉上不好合并，因为以每个点为根的时候这些深度是不一样的。

考虑这玩意有没有什么牛逼性质，比如直接换根什么的?想了想，从父亲走到儿子是子树深度\(-1\)，子树外深度\(+1\)，于是干脆变成子树\(-2\)。也就是说，我们需要支持子树\(\pm 1\)，查询有多少个独一无二的值。

注意到一个子树的深度是连续的，所以我们可以直接随手维护，每次只有两边会发生变化。然后只需要开个桶维护这些点就行了。

但是怎么知道这些点是哪些点?考虑以\(u\)为根的时候，只有\(u\)开头的长链上可能有独特的点，而长链的另一端一定是某个直径端点，于是跑两遍，分别处理到两个直径端点的路径即可，呃这么说可能有点奇怪，就是从两个直径端点出发换根。复杂度线性。

loj3153~3155 joi open 2019

A. 三级跳

查询区间中所有满足\(i<j<k,j-i<k-j\)的\(a_i+a_j+a_k\)最大值。

5e5 4s，考虑啥呢?

subtask3怎么做?枚举一个\(j\)之后，变成了\(2j<i+k\)，看起来是个\(\max,+\)卷积。枚举另外两个看起来是一样的。咋回事呢?

呃这不是\(\max,+\)卷积，这是\(\max,+\)卷积的后缀\(\max\)。算这个是不是经典问题?

好像不是。完蛋了。

考虑有没有什么性质。这个题看起来还略微有点像是那个区间最小\(\vert a_i-a_j\vert\)之类的。经过一些筛选之后，也就是说我们拿一些必要条件来约束之后，可能的三元组可能会变得很少。

为了支持区间查询，我们在构造约束的时候，一定是构造\(i^\prime,j^\prime,k^\prime\)使得\(a_{i^\prime}+a_{j^\prime}+a_{k^\prime}\geq a_i+a_j+a_k\)，且\(i\leq i^\prime,k^\prime\leq k\)。考虑第一段可以缩短，但是第二段不能缩短，于是我们可以想到，如果\(i,j\)不是区间\([i,j]\)的最大值和次大值，那么选取实际的最大值和次大值必然更优。

于是考虑两个端点分别是区间最大值和次大值的区间有多少个。你发现这居然只有\(O(n)\)个，因为考虑了几下你发现我们可以在一个区间的次大值那个端点处统计它，这就结束了。

呃怎么结束了?扫描线扫就是了。

B. 汇款

枣枣枣之言可谓切中了肯綮。注意到这个类似于进位，问题在于最高位可以进给最低位。这怎么办呢?

我们当作没有这样的进位，然后可以求出这两个数的差，那么根据这个差可以求出从最高位到最低位进位的量(每次进位会减少\(2^{n-1}-1\))，于是就破环成链了。

呃这个差可能非常大，怎么办?牛迭法法塔（不是

考虑这个除法有啥性质，它相当于每次拿出最高位来\(-1\)，然后让最高位后面第\(n\)位\(+1\)，于是我们只需要直接这么做即可，这是经典问题。

兔的题解是带状高消，看起来并不是非常本质相同（

C. 病毒实验

这个题好像非常经典，但是我没做过（

800 1s，好像想不到什么。

考虑一个很经典的事情，如果我们点了A之后，A会感染B，那么我们直接点B一定不劣。于是模拟出每个人第一个感染的人，这会形成一个DAG，DAG上每个SCC的答案是一样的，只有没有出度的SCC才有可能有贡献。

如果是求最大的话已经做完了，因为那样就是直接点B一定不优，于是每个点只会搜一次。这就出到模拟赛里/jy

这个没有出度的SCC 可能有多少个?如果它很少我们就赢麻了。

然而它实在是可能很多，构造方法是用一些0来把人们分开。这就完蛋了。

还是考虑怎么快速模拟。注意到一个人会不会被感染，只跟周围四个人有关，而我们可以爆力求出周围四个人在哪些情况下会让这个人被感染，也就是进行16遍模拟，每次模拟两轮，求出一个情况能感染掉的最大抵抗力。

于是现在我们进行强力模拟，每次让一个人被感染，就判断他周围四个人，这样复杂度是\(O(n^2)\)。还需要枚举人，于是这玩意不可能过。

考虑一个牛逼做法，我们对每个人，模拟前100个感染的人，他感染到的这些人都不比他劣。然后再跑那个SCC，此时没有出度的SCC个数将会非常少。

能不能估计一个数量呢（

看起来这个数量不可能超过\(\frac{rc}{100}\)，因为每个没有出度的SCC至少需要100个点。

这让我们发现了一些有趣的事情。考虑类似boruvka的做法，我们先找到每个人A感染的随便一个人B，然后将A合并到B这样的，现在问题是每个集合有一个最优的人，怎么快速选择这个人之后，在这个集合之外感染的第一个人。

我们对于每个集合，求出选择它里面最优的人之后，这个集合会被怎么感染，合并的时候直接重构复杂度就是对的。然后在集合边界上枚举即可。复杂度\(O(n^2\log n+m)\)。

loj3252~3256 joi 2020 final

近代joi了（

A. 只不过是长的领带

二分答案，然后每个人有一个可以戴的区间，我们的任务是ban掉每一个，然后得到一个完美匹配。定长分块优化建图，跑一个dinic，然后强行退流并再次增广，复杂度飞了。

太离谱了。考虑能不能直接贪心而不是dinic，你发现可以。

考虑能不能批量做这个贪心，你发现还是可以，正着一遍倒着一遍就行了，因为区间都是等长的。做完了。

诶是不是不需要二分?好像是的（

B. JJOOII 2

相当于找到一个最短的子串，使得它包含一个k级joi串。

考虑这个咋做，我们枚举第一个位置，然后往后在子序列自动机上跳就行了。现在问题是怎么才能快速跳\(k\)次，开vector即可。

C. 集邮比赛 3

走到的肯定是一个区间，区间dp。

D. 奥运公交

边数很大，我们需要缩小枚举量。

显然翻转的这条边，翻转之后会改变\(1\)到\(n\)的最短路或者\(n\)到\(1\)的最短路。注意这两个是可能都改变了的（

考虑这样的边能有多少以及怎么求，你发现数量会很大，但是一个最短路树就都搞定了。具体一点就是，我们可以借助最短路树\(O(n)\)算出一条边翻转之后新的最短路，于是枚举即可。

E. 火灾

数据结构题/hanx

考虑subtask2怎么做，你发现只需要求出每个位置影响到哪里就好了。

然后你发现每一个位置会一直往后影响到后面第一个比它大的。我们只需要求出来影响了多长，然后覆盖一下。

考虑subtask3怎么做。我们查询一个时刻的时候，考虑它前面所有能延伸到它这里的，也就是从它往前看的所有后缀\(\max\)，这个确实是单调栈的工作。我们可以在单调栈上二分现在是哪个覆盖过来了。

区间查询的话，我们先差分变成前缀查询。

注意到每一个连续段有四种可能 :

左边不动，右边伸长
左边缩短，右边伸长
左边缩短，右边不动
消失了

每一段都会经历这四个过程，当然其中有的过程可能持续了0时刻。可以一边扫一边用set维护每一段。

于是查询的时候直接做即可。这看起来还是很复杂，但是反正我只是在胡（

loj3361~3363 joi open 2020

joi的官方题解好像需要梯子才能看到/yun，可以在QingyuOJ(qoj.ac)上找到这一场的题解，其中B还是非常有趣的。

A. 家具摆放

这是一个非常经典的问题，原题是 XXI Open Cup, GP of Korea B. Cactus Competetion。

结论是，能走过去，当且仅当没有一行没了，没有一列没了，没有一个拐挡住了起点，没有一个拐挡住了终点。容易归纳证明充分性，但是问题是，谁会想到这个题需要拿必要凑充要呢?

剩下的问题是拐怎么维护。想了想感觉居然有点困难/jy

考虑插入一个新的1，要想找到一个拐，首先这个拐得经过这个1，于是数量变成了\(O(n)\)。但是1e9过不去（

我们维护每一行和每一列的极长前缀1，这个可以BiT搞定。然后分别考虑拐的顶点在新的1所在的行和列上的情况。以行上为例，我们维护了每一列的极长前缀1，只需要查询这一行的极长前缀1范围内，各列极长前缀1是否有足够长的，也就是求一个最长的，这个可以用BiT维护，需要支持撤销一步。总复杂度\(O(q\log n)\)。

B. 黑白点

这玩意看起来很像csp2021 D 交通规划（

然而还是不太一样，因为这个趋向于往外走。

考虑这个有点像AGC018D，但是又完全不像。

这里先讲一个类似于AGC018D的思路。考虑一条线段\((i,j)\)，它上面的交点个数不会超过它两边点数的较小值。如果我们可以让所有的交点个数都取到这个较小值，那么就必然最优了。

考虑什么情况下可以取到。不妨假设\(i\)是白色，\(j\)是黑色，\(i<j\)，并且\(i\)到\(j\)是短弧。那么对于\(i<k<j\)，考虑钦点如果\(k\)是白色则连到比\(i\)小的位置，如果是黑色连到比\(j\)大的位置，也就是说我们连的是递增的，或者说把黑点们任意循环移位之后(当然移白点是一样的)，第\(i\)个白点连第\(i\)个黑点。

后面就和后面一样了。

这是一开始的想法。

交点有啥性质?不知道。

考虑啥时候会出交点，我们知道如果两对\((i,j),(k,l)\)满足\(i<k<j<l\)或者\(k<i<j<l\)就会出交点。也就是说，我们需要找一种配对方案，使得每一对都满足\(s_i=s_j\)，并且满足\(i<k<j<l\)的两对数最大。

先想一个多项式做法。

注意到如果有两对满足\(i<j<k<l\)的\((i,j),(k,l)\)，那么我们可以调整一下变成\((i,k),(j,l)\)，这样本来跟它俩中的两个相交的，现在还是跟两个相交；本来跟一个相交的，现在还是跟一个相交；本来不相交的，现在还是不相交，或者可能变得相交两个。但是这样的调整可能是不可行的，因为可能\(i,k\)是白色而\(j,l\)是黑色这样的，换了配对就会出问题。

然后就不会了。看看题解，好离谱（

考虑根据上面这个结论可以知道，最优策略一定是把所有黑点和白点的位置分别找出来，任意破环为链之后，第\(i\)个黑点匹配第\(i\)个白点。上面的结论其实是说明逆序对一定不优。

然后我们就会\(n^2\)了，考虑怎么进一步优化。

考虑一个牛逼结论，在这个构造中，跨过一条线段的边数，恰好是两边点数的较小值。这是显然的。

然后呢?设白点序列是\(a_i\)，黑点序列是\(b_i\)，那么我们就枚举\(k\)，钦点\(a_i\)匹配\(b_{i+k}\)即可。最后答案看起来像是

\[\max_k\sum_{i=1}^n\min\big((b_{i+k}-a_i-1)\bmod{2n},(a_i-b_{i+k}-1)\bmod{2n}\big)\]

这个\(\min\)上会发生若干次切换，当然每个\(i\)只会切换最多两次。

考虑一个\(a_i\)对每个\(k\)的贡献，它在一些位置贡献\(-a_i-1\)，一些位置贡献\(a_i-1\)，一些位置贡献\(-a_i-1+2n\)，一些位置贡献\(a_i-1+2n\)。

考虑一个\(b_i\)对每个\(k\)的贡献，它在一些位置贡献\(b_i\)，一些位置贡献\(-b_i\)。

然后就做完了，维护三个指针硬扫，复杂度是线性。

C. 发电站

感觉上是说，如果一条链的端点都被打开了，那么中间就都会损坏。

注意到我们几乎不可能让一个发电机坏掉，除非它确实需要坏，比如在菊花中，中间那个必须坏掉，这样我们可以选择所有的叶子。

注意到有的基站没有发电机，这说明我们可能选择一条长链。

我们可以取消选择所有不爆的，于是可以考虑选的时候就让它不会爆。

强行树形dp。考虑如果一个点选了，要么它子树外都不选，要么它子树内都不选；如果一个点没选，那么它的各个子树都可以选，子树外也可以选。设\(dp(u)\)表示在\(u\)子树外还能选的前提下，\(u\)子树内的最大收益，于是它应该和\(a_u\)取一个\(\max\)，表示只选自己，这里\(a\)当然表示发电机数量。考虑转移，那就是直接把每个子树加进来，最后减去\(a_u\)。

然后考虑在每个方案的lca处统计答案。

如果lca选了，那么lca只有一个子树可以选，我们必然取最大的子树
如果lca不选，那么每个子树可以自由选择选或者不选

强行转移即可。然而这个题想了半天，看了题解一眼是dp才想到要强行dp，我还是naive了/ll

当简单方法都解决不了了，再去发现性质，并且每发现一个性质，都应该回去再看一遍所有的简单方法。我觉得我这话说的很好。

loj3468~3472 joi 2021 final

A. 有趣的家庭菜园 4

看起来就是严格单峰的。

呃直接从两边往中间模拟即可。

B. 雪球

因为所有雪球都是一起移动的，所以如果一个雪球走到了别的雪球走过的地方，那么它往回走才可能继续走到雪上。

考虑我们对每个雪球求出它第一次走到左右雪球的轨迹上的时间，这个可以直接二分得到。做完了。

呃注意到这是对于一个序列的多次二分，于是或许可以用什么技巧优化到线性/yiw，不过我也懒得想了（

C. 集体照

只有5e3。是不是随手啊!

注意到高度是排列，所以如果有问题，那么只能是相邻的两个人，一个高\(x\)，一个高\(x-1\)。于是整个序列划分成了若干个下降的连续段。只需要按值域扫描线，设\(dp(i)\)表示放了前\(i\)个人，他们是\([1,i]\)的最小逆序对数，转移就是枚举\(i\)所在的下降连续段，然后因为这是每次加入一个，容易二维前缀和计算贡献，至少感觉上是这样的。

D. 机器人

除非不连通，否则不可能无解。

考虑首先我们肯定不会一个点走两次，所以只需要把走一条边的代价赋成把它的颜色改成独一无二的代价。注意到走的每条边，要么是原来的颜色(把同色的都改掉)，要么是改成同色权值和最小的颜色(然后把同色的都改掉)，要么是改成次小的(因为有两条边，这两条边颜色也要不同)。

于是把每个点拆成三个点，表示入边是原来的颜色，最小的颜色和次小的颜色即可。

不过这个东西假了，因为如果入边是原来的颜色，我们选择了一条和入边颜色相同的出边就不好处理了，因为此时我们并不能让把别的同色的改掉这件事变得容易描述。

考虑一个牛逼做法，我们给每个点建度数个虚点，表示进来的颜色，于是就结束了。

E. 地牢 3

又是数据结构题/se

这让我们想起一个经典题叫Organizing a Race，但是这俩还是完全不一样。

爆力怎么做，爆力是不是，直接最短路!(呃当然这个最短路实际上是dp)

贪心地，我们只可能做两种购买，恰好撑到下一次买，或者买满。于是现在每次查询只有\(O(n)\)状态数了(每个只会贡献一个状态)，双指针扫一扫建立状态，单调队列优化转移，复杂度是\(O(nm)\)。

然后呢?你发现给\(O(nm)\)的subtask1只有11pts，我们的做法是不是过于复杂了（

考虑加强这个结论。容易想到，考虑在\(i\)买一次，能走到的区间设为\([i+1,j]\)，考虑这个区间中第一个满足\(b_k\leq b_i\)的\(k\)

我们肯定希望加到恰好能走到\(k\)，因为这样一定不劣。
如果不存在这样的\(k\)，那么我们会加满，然后走到\([i+1,j]\)中最小的。

这个策略感觉上很对，于是我们现在可以知道每个位置有一个\(\mathrm{next}\)。然后就是经典做法，这个\(\mathrm{next}\)构成一棵树。

在\(u\)上扫描线，然后用类似弹飞绵羊的方法来维护，每块开一个lct，超出块的直接查，复杂度\(O(n\sqrt{n\log n})\)。

考虑\(\mathrm{next}\)的切换只会发生\(O(n)\)次，这是因为\(\mathrm{next}(i)\)的取值就是从右往左单调栈的时候\(i\)弹掉的所有元素和\(i\)之后的第一个元素。除了\(i\)之后的第一个，别的都弹掉了，于是总切换数就是\(O(n)\)。整个用一个lct来维护即可，或者如果你想，也可以根号重构什么的来降低现场的代码难度（

loj3520~3522 joi open 2021

A. 杂交

先考虑只有一次询问怎么做。

考虑构造一个什么结构满足J+J=J,O+O=O,I+I=I,J+O=I,O+I=J,I+J=O。

你发现这个结构性质不好，因为打表可以发现它不是结合的，简单的反例是(J+J)+O=I，而J+(J+O)=O。没有结合律意味着很多事情都不能做，比如它不可能和一个我们熟悉的结构同构。

能不能强行考虑?考虑三个串可以生成什么样的串，这可以随三个然后搜一搜。我搜了一个长5的，用xorshift64生成。

看起来很有趣……呃啥也看不出来。

换个种子试试。

呃为什么还是六个?换个长度试试。

草，离奇了（

一共只有九个串。用线段树维护一下对于每一个串，区间不对的个数就彳亍了。

B. 决算报告

一眼没看出A的我 : 没想到吧，这才是签到题（

直接dp即可。

呃这可吗?好像不可。

哦这是可的。考虑设\(dp(i)\)表示以\(i\)结尾，并且\(i\)作为最后一个前缀\(\max\)的最大得分，转移的时候，如果要从\(j\)转移过来，那么要求\(j\)到\(i\)之间没有一段长\(d\)的比\(a_i\)大的数。先扫值域预处理这个东西，然后直接线段树优化转移即可，复杂度\(O(n\log n)\)。

C. 怪兽游戏

1e3个数，1e4次调用，看起来很紧啊，于是我们确实需要紧的排序。

先想点性质。

有两个想法。第一个是考虑直接按照这个排序之后会出什么问题。你发现它会分成若干段连续下降的，而这些段之间看起来是上升的。

第二个是直接考虑一个方法。你发现常见的排序中，只可能是拿归并/二分插排/选择来做，但是考虑了一下二分插排肯定没前途，选择要开数据结构也没前途(因为数据结构比归并复杂?)，所以考虑归并。

但是你发现归并是归并不了的，因为如果我们遇到了不对的那就完蛋了（

于是先考虑第一个想法。我们先进行一次归并排序，实现的时候注意一点(就是别瞎比)，就可以达到9e3次询问以内，于是我们还有1e3次多可以用。结论是，归并排序比较次数最坏是\(n\lfloor\lg n\rfloor-2^{\lfloor\lg n\rfloor+1}+n+1\)，大约就是\(n(\lg n-1)\)，这里精确计算之后是\(8953\)次。

随一些试一试，你发现排出来的确实满足我们一开始考虑的性质。注意最终的序列也可以看成随机的，因为我们一开始可以把它随机打乱，这样spj应该很难卡出奇怪的边界情况?

考虑接下来怎么用\(O(n)\)次找到这些反着的段，接下来我们只需要把它们全都翻转就好了。我们只需要找到所有两边的数不在同一段的间隔。

先注意到一个性质，排序之后必然不存在相邻的两个长\(1\)的段，或者说相邻两段的开头差不可能是\(1\)，这可以随一随验证。呃更强一点的结论是，排序之后相邻两个总是满足题目给的顺序。

考虑我们现在处理了前面若干段，设当前这一段是\([l,r]\)，我们需要区分下一个是\(l-1\)，还是比\(r\)更大(也可能是\(r+1\))。

如果\(r-l+1\geq 3\)，那么我们只需要拿\((l,r)\)内任何一个问一次。

如果\(r-l+1\leq 2\)，那么我们拿\(l,r\)问没有什么用。怎么办呢?考虑我们不要拿这一段和下一个问，我们问出这一段的结尾是不是真的结尾，这就需要用到上一段的开头\(x\)，如果\(x+1=l\)那就是真的结尾，否则不是。

但是对于第一段，它是没有上一段的。不过注意到我们只需要搞定前三个是不是在同一段就行了，而题目中给了一个有趣的限制\(n\geq 4\)，这就让人浮想联翩了。

注意到排序之后，每个前缀的值域都是连续的，所以和排列是一样的。考虑长\(4\)怎么做。

呃这是废话，我们只需要做所有的比较，然后搜一个排列满足条件就行了。当然你可以搞点牛逼做法，但是搜确实没有思维量（

最后比较次数是大约\(8953+6+997\)之类的，看起来很可以过。

loj3538~3541 joi open 2018

A. 冒泡排序2

冒泡排序轮数显然是经典结论，但是我不知道的话还能怎么办呢（

考虑如果只问一次怎么做。那也不会/fn

考虑冒泡排序的过程就是尝试往后移动第一个，直到碰到一个比第一个更大的，此时再把这个更大的往后移动。把移动画成折线，这让我们想到一类经典题，这个可以用一个栈来从右往左处理每一个的移动。

但是这个不对，因为这不是移动，而是交换，有的数会往前走。这就比较复杂了。

考虑有没有什么结论。能不能直接指出一个数会移动多少轮?考虑对它的一轮移动之后，它会跨过若干个比它小的……然后好像没啥性质。

反过来，我们考虑它跨过的这些数。每个数每轮恰好被跨过一次，所以一个数被跨过的次数就是前面比它大的数的个数，答案就是这些的\(\max\)。

呃这个问题看起来就很简单，每次修改是两个2-side矩形的加减，要求全局\(\max\)，k-dt冲就是了。

考虑怎么更好地维护这个，你发现难度实际上挺大的，因为问题是三维的。可能需要找一点性质。

你发现如果\(i<j,a_i>a_j\)，那么\(j\)被跨过的次数必然比\(i\)多，于是只有所有后面没有比它小的数的数，也就是所有的后缀\(\min\)才会有贡献。除此之外看起来并没有别的性质。

这个修改让我们不能容易地维护所有后缀\(\min\)。弃了弃了。

有没有什么别的转化?

搞不定了。题解给出了离谱的转化，既然这个\(\max\)总在后缀\(\min\)处取到，而这些后缀\(\min\)们，后面的数不比它们小，于是只有前面的数比它们小，而设一个后缀\(\min\)是\(a_i\)，有\(x\)个数比它小，而它前面有\(i-1\)个数，那么前面就有\(i-1-x\)个数比它大。而如果一个数不是后缀\(\min\)，它后面还有比它小的，于是算出来的贡献只会更小不会更大，所以我们按照这个\(i-1-x\)算就是对的。于是砍去了一维，一个线段树就搞定了。是不是也可以BiT?

B. 猫或狗

别想性质，直接ddp。

C. 山体滑坡

¿动态图连通块数¿支持删一车边再加回去¿

一开始一直读错题（

注意是6s。

考虑这个咋做，你发现我们需要查询只加都在一个前缀和一个后缀的边的连通块数，前缀和后缀是独立的，于是我们可以考虑数据结构维护这个东西。接下来只考虑前缀。

先对时间进行线段树分治，转成插入和撤销。

呃除了直接线段树分治，另一个想法是，使用消失之物的分治。我们递归右半边的时候，加入左半边向左连(包括连到左半边内部)的所有边，回来的时候撤销，递归左半边则什么也不做(因为只考虑前缀)。这可以处理静态的单次询问。

考虑各subtask都怎么做。1是爆力，2的性质相当于左右是完全割裂的，于是可以直接线段树分治，一边跑一边缩点，复杂度是一个\(\log\)。3看起来是省去了线段树分治，不过剩下的部分还是不好做。

考虑两个分治结合是不是可以把它秒了。你发现也许是可以的。我们外层时间分治，内层序列分治。为序列分治建一个线段树，每次插入一条边，就走到所有它产生贡献的位置(也就是沿着根走到它的右端点的位置，路径上所有点的右儿子，如果右儿子也在这条路径上则不算)，给它们的子树打一个插入这条边的标记，而撤销一条边则会撤销这\(\log\)个标记。

呃子树打插入一条边的标记简直是丧心病狂了，不过我们仍然不是不可以做。查询的时候，从根往下走，一路上记录所有的标记。呃你发现这相当于把所有没被影响的边打成\(\log\)包了，这些包压根不好处理。

考虑能不能内外层换一换。我们外层序列分治，内层时间分治。往右走的时候，我们在时间上插入了若干个区间，每条边会拆成\(\log\)个相同的区间，而走回来的时候会撤销这些。考虑内层的时间线段树怎么维护在一个时间区间上插入这件事，你发现还是维护不了，同时你也发现序列分治和时间分治是相似的。

你也发现动态的消失之物是困难的（

poly log还有前途吗?这总是要基于时间分治，而时间分治之后很容易想到序列分治，但是这个序列分治并没有很好的扩展性，这本质上是连通性没有任何可以快速合并的性质。于是考虑换一个。

我们先考虑一个牛逼性质。插入一条边\((u,v)\)会产生什么影响?在\(v\)之后的查询答案会\(-1\)，但是到某个位置就不减了，这个位置就是第一个用已经插入的边就把\((u,v)\)连通了的位置，也就是\((u,v)\)之间所有路径中，右端点最大值的最小值，这是瓶颈树。于是我们只需要用树数据结构维护mst来查链\(\max\)，然后用BiT维护区间\(\pm 1\)，问题变成插入撤销维护mst，lct就行了。

但是这个线段树分治lct看起来很离谱，并且它看起来就是 city，所以有没有类似于 city 的一边分治一边收缩的做法?

呃感觉上可能有，但是没有兴趣了，因为这题6s，线段树分治lct是可以稳过的?没写过。不过就算它过不掉，我们仍然可以自豪地说得到了俩\(\log\)做法（但是没写过不知道正确性/jy

好像有简单分块做法，但是我不知道（

呃我大概知道了。对时间分块，每一块把之前的，并且这一块里面没有被删的边加进并查集，然后把这一块里面加上的和之前加的，这一块里面被删了的边连在并查集搞出的连通块之间，直接跑。复杂度好像是\(O(n\sqrt{n\alpha(n)})\)。

D. 木琴

怎么感觉又是倒序的（

极差让人想到笛卡尔树之类的东西。但是那个还是太复杂。

用\(p_i\)表示数\(i\)的位置。注意到给了一个牛逼性质，也就是\(p_1<p_n\)。这玩意有啥用?

考虑我们找到\(p_1\)。你发现这个只需要从右往左二分就行了。

然后我们从\(1\)出发往左右扫，然后你发现这个没啥性质。

考虑一个牛逼做法，我们把序列划分成若干上升段，然后问出每一段的开头，并从开头出发问出每个数。但是你发现我们不知道第一段是升还是降，于是就完蛋了。当然不止这一个问题。

考虑我们把序列划分成若干上升段和若干下降段，然后不需要知道第一段是什么，只需要往右扫，遇到转折就切换升降状态，然后就可以画出一条折线来，但是实际上它有两种可能。此时考虑到\(p_1<p_n\)，也就是说我们求出最大值和最小值，在前面那个就是\(1\)，后面的就是\(n\)。询问次数看起来是松的\(2n\)。

于是joi就做完了，下面是joisc。

难度骤增?

突然想写英文名了，那就开始写英文名吧（

感觉我每天来机房卷这些题，实际上就是因为不想考虑太多的事情，当我不卷的时候就会开始乱想……所以我会强行想每一道题，就为了找点事做，实际上这也确实让我很有事做。这可能一个月我已经写了超过两万字了。

loj2390~2401 joisc 2017

据说难度极高，也许堪比open cup?

最困难的题是Sparklers和Arranging Tickets。但是好像有不少老哥觉得Sparklers是套路题?不懂了，可能我格局小了。Arranging Tickets是真的传世经典。

A. Cultivation

\(n\)只有300/jy

考虑一个草长出来是啥形状，你发现它是一个矩形。如果它的长宽是\(r,c\)，那么需要\(r+c-2\)年让它长出来，并且风向的使用顺序是没有关系的。同时所有一开始的草在它扩展出的矩形中的位置是一样的。

\(r,c\)是1e9，于是考虑有什么技术可以减少枚举量到多项式级别。注意到最后一年一定是两个矩形相撞或者一个矩形撞上边界，于是考虑两个草要想相撞，可能的矩形位置很多，但是要么长已经确定了，要么宽已经确定了，这得到了\(n^2\)个长和\(n^2\)个宽。最后我们选择的长宽必然分别在其中，不然减少到其中最接近的必然仍然可以。

然后考虑长越长，宽不会变短，于是枚举长，双指针扫宽，这样我们需要\(n^2\)次检查一组长宽\(a,b\)是否可行，于是要求每次检查是\(O(n)\)的。这玩意怎么做到\(O(n)\)?

考虑先把每个草放在它长成的矩形的左下角，我们希望能从其中找到一个\(r\times c\)的矩形，然后希望可以做一些平移来使得所有的草都在这个矩形中的正确位置。容易感觉到然后的这一步是没有用的，也就是说如果能找到这么一个矩形，那么必然可以做这样的平移。

考虑如何证明这件事。能这么平移，当且仅当每个草在原来的矩形中的位置，贴到我们找到的这个矩形上去，恰好都在它们长出来的矩形们中。如果贴上去之后有一个不在它长出来的矩形中，那么所有的都不在它长出来的矩形中，也就是说每一个点都在别的点长出来的矩形中，我们随便钦点一个这样的矩形，那么\(n\)个点\(n\)条边，必然会成环。而平移是整体的，所以不可能成环，除非平移量很小并且它们一开始就很接近，此时必然还是每个都在自己里面。

所以如何判断是否存在一个\(r\times c\)的矩形?简单想法是把连续的缩起来，然后单调栈跑最大权子矩形，但是那样是\(O(n^2)\)单次，总共是\(O(n^4)\)。考虑有没有点牛逼做法。

所有的性质就是这个图形是一些\(a\times b\)的矩形的并。然后想了很久感觉上这并不是什么好的性质，所以我们就死了。/ll

考虑这个单调栈实在是没法优化，我们能在哪里改一改来避免最大子矩形呢?考虑扫完长之后不要双指针转成判定了，我们直接最小化宽，这玩意说不定会好做。

还是转成要能找到一个\(r\times c\)的矩形。

考虑我们不允许在纵向上的平移，也就是说固定纵向的位置是正确的，然后考虑横向的位置摆在哪里。扫完长之后，我们得到了若干条横线，每个横线会向上下扩展，于是这个情况看起来是这样的 :

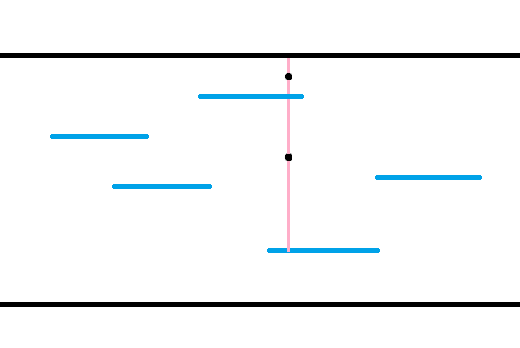
考虑每个点需要上下的蓝线扩展来覆盖它，于是如果上下都有线，这构成了一个对上下之和的限制，否则构成了对上下之一的限制。考虑我们处理每一列，把相邻的相同列缩成一段，用单调队列维护。枚举过程中蓝线会向右伸长，于是会有\(n^2\)次一段的消失，我们直接爆力维护这些产生和消失，每次去更新这一列的信息即可，单调队列扫一遍是\(O(n)\)，更新是也\(O(n)\)，总共是\(O(n^3)\)。

所以能否解释，为什么我们放弃了双指针，转而直接最小化宽度?实际上想法不应该是这样的，这是因为我们在枚举了长宽之后，自然地固定了长宽去考虑找到一个\(r\times c\)的矩形。实际上如果不固定长宽，更容易导出只允许横向的平移的想法。做完之后再看，感觉这个问题中有很多的维度，设上下左右的位移分别是\(a,b,c,d\)，我们可以得到的扫描线方向是

扫长，也就是\(a+b\)
扫宽，也就是\(c+d\)
扫草在它长出矩形中横向的偏移量，也就是\(a\)
扫纵向的偏移量，也就是\(c\)

一开始我们考虑的是前两个的组合，最后的正解是第一个和第三个。感觉一下，确实应该尝试这两种方向。

B. Port Facility

数数题/jy

打开tag一看，分治，二分图匹配，线段树，这啥啊/jy

还是从头考虑。如果只有一个栈，那么就会形成一个括号序列。现在有两个栈，那么问题是要划分成两个括号序列，求方案数。

\(n\)足足有1e6，玩个锤子（

多种括号的话，感觉上很不好做。考虑现在要把\((a_i,b_i)\)加入一个栈，那么完全包含在这里面的没有什么限制，在外面的也没有限制，但是跨过这个的就只能加入另一个栈了。

因为括号互不相同，可以看成一条线段，问题是每个栈里面的线段只能不交或者包含。现在可以尝试给出多项式复杂度的做法了。

想了想你发现我们并不能给出多项式复杂度的做法，因为沿着这个括号形成的树结构进行dp的话，体现在序列上是混乱的，不沿着树做dp又会需要存巨量的信息。

没办法了。观察样例，王卷王之言可谓切中了肯綮，答案似乎总是\(2^k\)。

想了想你发现，如果有三个两两相交而不包含，那么答案就是\(0\)。于是如果把相交关系画出来，不可能存在三元环，现在你知道为什么会有二分图匹配的tag了。

我们只需要求出有多少个连通块，每个连通块是一条链，上面必然是黑白交替地选，而链之间不会互相影响。做完了，复杂度\(O(n)\)。

呃还没有描述如何找到和一个相交的。这是一个2-side矩形，扫描线线段树即可，总共是\(O(n\log n)\)。或者可能有什么牛逼做法?

好像确实有牛逼做法，不过反正数据结构可以完全替代这里的思维（

C. Sparklers

考虑一定是两边都往中间跑，然后中间这个老哥会先往一边走，点了一炮之后，两个人必然是一个往左一个往右，然后就分开传递了。于是只有四种情况，也就是第一个人往左还是往右走，往另一边走的是返回的第一个人还是第一个人最先碰到的人。

二分答案，然后枚举一个情况，现在第一个人已经和某个人会面，并且决定了谁往左谁往右，接下来两边应该是一样的。

两边是两个接力的过程，每个人都会尽可能往中间走，遇到点着的人之后和点着的人一起往两边走直到火熄灭，在熄灭的一瞬间点燃自己。于是就做完了。

写一写你发现剩且仅剩一个问题，也就是前两个人在什么地方会面。这个位置向接棒的人靠近是有用的。比如说第一个人在右边，他要往左走传给左边第一个人，而左边第二个人离的非常远，于是我们就会希望第一个人多往左走一走。但是注意到，如果右边没有人了，那么我们直接让他尽可能往左走就行了；如果右边还有人，那么需要走的恰到好处，以至于往回走两步还能点上这位同志(当然她应该跟着往左走)。然后你发现这玩意需要在两边达到某种平衡，只需要另一个二分来搞定。你觉得我会写这玩意?

感觉上这个正确性问题不大，但是庭队长教育了我一下，我发现问题实际上还是很大的（

考虑一个牛逼结论，同时只有一个人会点着。考虑因为所有人都往中间走，所以在原地等着的话，所有人都在靠过来。

如果两个人分开往两边走，那么虽然速度变快了，但是能走的时间也变短了，算一算你发现往两边走是不优的。
如果两个人往同一边走，那么显然是两个人一起走，没点的老哥蹲一波，等烧着的老哥烧完了再点更优。

于是考虑接下来会发生什么。既然只有一个人会点着，那么我们可以认为点了一个人就是拿他续了\(t\)时间，然后他就没了。

然后我们又可以发现一个性质，也就是前面说分头往两边走不优，原地等着更优，而现在可以发现如果接下来需要往两边走，那么直接往两边走更优，也就是说我们是不会停下的。

现在仅剩的决策是每一步往左走还是往右走。

容易想到区间dp，设\(dp(l,r,0/1)\)表示把区间\([l,r]\)都续掉了，现在和\(l/r\)在一块，是否有可能。

注意到比如现在和\(l\)在一块，这个过程一定是走到极右把\(r\)续了之后，一直往左走找到了\(l\)。注意到走到\(r\)之前，\(r\)一直在往左走，走到\(l\)之前，\(l\)一直在往右走，而此时如果\(r\)阴魂不散跟着第一个人走，那么\(l,r\)刚好相遇。于是我们知道此时第一个人和\(l\)必然在\(l,r\)的中点\(\frac{x_r-x_l}{2}\)，并且时间就是\(\frac{x_r-x_l}{2s}\)，那么第一个人还剩\((r-l+1)t-\frac{x_r-x_l}{2s}\)时间。所以说我们其实没有必要记那个\(0/1\)。

如果不二分，这就是\(n^2\)了，但是转移要复杂一点。

为了优化复杂度，你发现这个好像没有什么性质，于是我们考虑一个别的做法。

考虑从\([l,r]\)尝试扩展到\([l-1,r],[l,r+1]\)中的某一个。根据刚才的转移，我们知道，能扩展到\([l,r+1]\)，当且仅当\(\frac{x_{r+1}-x_l}{2s}\leq(r-l+1)t\)，也即\(x_{r+1}-2st(r+1)\leq x_l-2stl\)。于是设\(a_i=x_i-2sti\)，那么可以往右扩展一步就是\(a_l\geq a_{r+1}\)，往左就是\(a_{l-1}\geq a_r\)(而不是\(a_r\geq a_{l-1}\))。

现在我们把它转化成了，每一个位置有一个权值\(a_i\)，一开始你拿着\([k,k]\)，你可以选择往左或者往右扩展，需要始终满足\(a_l\geq a_r\)，问是否能扩展到\([1,n]\)。

首先，如果我们往左扩展一步或者很多步之后，\(a_l\)增大了，那肯定是好的，右边减小也是一样的。但是如果两个都不彳亍，我们就不知道该怎么办了。

考虑一个想法，我们每次尝试尽可能往左扩展，直到遇到一个比\(a_l\)大的位置，把它作为新的\(l\)。然后尝试尽可能往右扩展，直到遇到一个比\(a_r\)小的位置，把它作为新的\(r\)。两边轮流这样扩展即可。如果扩展失败了，也就是说遇到更优的之前就扩展不动了，容易发现此时必然无解。

吗?如果没有更优的，我们就完蛋了。考虑\(k\)左边的最大值\(a_L\)和右边的最小值\(a_R\)，如果你扩展到了\([L,R]\)，那么接下来你的扩展不可能会扩展到更优的地方了。当然贪心地，你肯定会经过\([L,R]\)这一状态，如果你扩展不到这一状态，那么肯定无解了。

接下来是另一个非常牛逼的想法。我们时间倒流，你发现收缩和扩展是完全一致的，于是我们从\([k,k]\)扩展到\([L,R]\)之后，再从\([1,n]\)开始尝试收缩到\([L,R]\)，如果两个都成功了那就成功了，否则无解。

然后我们就线性地check了，总复杂度\(O(n\log v)\)。

没有人当场过这个题。

A. Arranging Tickets

无敌思维题。收录于 zroi noip18联测。

看了一眼发现没收录?离谱了。那就收录在这吧。

大概是说，圆分成\(n\)段，给定了若干个弧，你可以选择选这半弧还是那半弧，要让被覆盖次数最多的段覆盖次数最少。

结论是，我们先让所有弧都选顺时针，现在\(n\rightarrow 1\)的弧没有被覆盖，然后我们尝试翻转一些。如果两个弧不交，那么画一画你发现，我们不会把它们都翻了。于是所有翻转的弧有交。同时，翻不翻是对称的，所以所有翻转之后的弧也有交。

然后你发现这个结论还不够用。另一个显然的结论是，都选了顺时针之后，要么都不翻，要么被覆盖次数最多的地方一定会翻。然而这个没啥用。

对称的结论是，都翻了之后，被覆盖次数最多的地方不会全翻。然而这个也没啥用。

题解给出了非常牛逼的性质，不知道是随出来的，还是说揭示了什么结构上的性质。我尝试理解这些结论，并写出一个人类可以理解的思路，虽然场上仍然几乎不会有人能想得这么深刻。

考虑翻转之后会发生什么变化。我们找到翻转前覆盖最多次的段\(t\)(们)，以及翻转后覆盖最多次的段\(t^\prime\)(们)。刚才我们知道所有翻转的段都有交，设这个交是\([l,r]\)，这是它们翻转之前的交。

考虑我们希望通过翻来减少的就是\(t\)们，于是每翻一个弧，它必然覆盖所有的\(t\)，否则则会导致一些\(t\)的覆盖次数减少了，而另一些反而增加了，那么答案反而增加了，我们肯定不希望这样的事情发生。这样所有的\(t\)都在\([l,r]\)内了。

考虑知道了某个\(t\)我们可以干什么。二分答案\(d\)，然后考虑如何判断。

我们枚举\(t\)这个位置最后被覆盖多少次。感觉上\(t\)被覆盖的次数应该非常接近答案，因为我们答案的瓶颈就是\(t\)被覆盖的次数。我们直接猜测它要么就是答案，要么比答案小\(1\)。证明也不困难，注意到如果它比答案小了至少\(2\)，那么我们可以把一段翻回来，这不会让答案变大。

于是分别钦点\(t\)被覆盖\(d\)或\(d-1\)次。这样还满足单调性吗?讲道理是满足的，因为如果存在答案更小的方案，只需要把更多的段翻回来就好了。但是这个也要求我们必须把二分上界设为一开始覆盖次数的\(\max\)。

于是我们会进行的翻转次数也确定了，因为每次翻转总是让\(t\)的覆盖次数\(-1\)。

但是尽管有了这么多东西，我还是不会做（

考虑把所有经过\(t\)的弧拿出来，进行一个牛逼贪心。

从左往右扫，只考虑跨过\(t\)的弧，尝试满足\([1,t]\)都\(\leq d\)的限制。如果\(i\)这个位置覆盖了\(a_i\)次，那么每次经过它的翻转会让\(a_i+1\)，而不经过它的会\(-1\)，假设我们刚才算出来的总反转次数是\(s\)，那么为了让\(a_i\leq d\)，设经过它的翻转次数是\(c_i\)，就需要满足\(a_i-c_i+(s-c_i)\leq d\)，于是我们知道\(c_i\geq\lceil\frac{a_i+s-d}{2}\rceil\)。如果\(i=t\)，则需要按我们钦定的覆盖次数来。

于是我们扫到\(i\)的时候，需要拿出左端点在\([1,i]\)的弧们尝试满足这个限制，当然前面可能已经覆盖了一些，这个一边扫一边就维护掉了。如果前面覆盖的不够，我们希望拿出来翻转的弧对\([t+1,n]\)的影响尽量小，于是用一个堆维护这些弧，每次拿出右端点最大的来翻转。最后再用差分-前缀和检查一遍\([t+1,n]\)即可。

这就做完了，复杂度\(O(n\log^2 n)\)。

B. Broken Device

loj上好像没有调好通信，可以在atc https://atcoder.jp/contests/joisc2017/tasks/joisc2017_e 找到。

通信题。

Anna每天有一个1e18以内的数字，要把这个数字发给Bruno，方式是发一个150位的二进制数。

每天Anna的机子会坏掉，这导致有最多40个bit发出去总是0。Anna可以知道有哪些位置坏了，但是Bruno并不知道。请你帮助Anna完成任务。最多有1e3天。

这个问题是不是很经典啊（

经典做法是，随一堆数然后用线性基来凑。

发送1e18只需要60位，有40位坏了，那么还有50位可以夹带私货。

考虑如果可以发很多位怎么做。我们可以发很多个1，比如1e18个，然后Bruno数有多少1。

于是这让我们很容易想到考虑一个几乎和0无关的编码方法。我们用一段0表示分割，一个1或者两个1表示二进制的0和1。这样可以发多少呢?如果没有坏掉的位置，我们可以发50个bit，如果有则最少也能发30多个，可以表示也许1e10?

现在有两条路，也就是夹带私货指出坏掉的位，或者考虑0的数量和位置不影响信息表示的编码方法。

夹带私货这方面，好像有某些经典技巧，比如什么分块，然后一块坏的太多就扔掉之类的，这实际上也是使得0的数量和位置不影响信息表示的编码方法。考虑这里有40个坏的，50个用来夹带私货，那么我们两个一组，如果这一组里面有坏的，我就让它全是0，否则我让它至少有一个1。每组有三种可能，也就是11 10 01，现在我们剩下最多35个可用的组，这可以表示5e16。¿

计算器算了一下，我们只需要38位就行了。

考虑三个一块，这样每块可以表示7种情况。但是我们只剩下10个可用的块了。完蛋。

考虑能不能把那些坏掉的块回收利用一下。考虑只坏了一个的块，注意到要么有一半的块坏第一位，要么有一半的块坏第二位，于是我们可以平移一下让更多的块坏第二位。但是这没有用，因为我们无法区分一个只有第二位坏了的块，和一个全都坏了的块。

如果我们不作区分呢?按照上面的11 10 01来搞，如果下一块坏了，但是它的信息刚好可以填10 01中我们要的那一个，那么我们就起用。只需要38个三进制位，这个方法能不能挤出这3位呢?我不知道。

去看看这个能拿多少分。你发现这是85pts，第三档的最高分。

题解给出了一个牛逼修补方法。我们搞若干个\([0,10^{18}]\leftrightarrow [0,10^{18}]\)的随机双射，Anna使用这个双射进行随机打乱，Bruno则使用逆来还原，这样就有很大的概率可以挤出3位。怎么搞这个双射?两个人用同样的随机数生成器，每一轮随机一个偏移量即可。

考虑三个一块的做法能不能救一救。这个方法非常牛逼。我们希望完好的块表示两位，而坏了一个的块表示一位，000表示没有信息，那么完好的块需要对应四种三位，坏了一个的只有三种了，想一想你发现这三种必然不可能成功。

考虑我们怎么让它多一点。考虑把完好的块对应的四种借用一点过来。具体地，给出一种可能的构造 :

如果这是一个坏了一位的块
- 如果坏的不是第一位，用100表示1，110/101表示0。
- 如果坏的是第一位，用010表示10，011表示11。
否则用010表示10，011表示11，001表示00，111表示01。

就结束了。

C. Railway Trip

考虑这是一个图，然后我们在上面跑最短路。

注意到每次停车都可以换乘，于是我们只连到第一步可以走到的车站。类似于 joi final 2021 E. 地牢3，这个图只有\(O(n)\)条边，每个点连到从它出发左右的前缀\(\max\)，直到这个前缀\(\max\)比这个点要大了就停止。

于是现在我们可以处理\(q\leq 50\)。

我们将连向左右第一个比这个车站大的车站的边称为上升边，别的是下降边。考虑这个过程一定是，进行一些上升，然后从高空跨过去，然后进行一些下降，可以把每个车站以流量作为高度画出来，直观地得到这个结论。上升的时候也可能走下降边以得到更快的上升。

但是这个没啥用，因为它只是整体上升/下降，我们没法明确区分这两段。考虑是不是有什么牛逼性质，比如上升的时候其实只会走上升边?

这时候我们终于动了动脑子，于是立刻发现一个非常离谱的事情 : 上升边是下降边的反边。fuck。

于是我们只需要连左右第一个更大的了。这让我们想起很多题，比如六元环或者雨林跳跃之类的。

考虑使用卡笛尔树。建立大根卡笛尔树，那么每个点会向左子树右链和右子树左链连边。于是没有跨过子树的边，于是我们可以求出卡笛尔树上两个点的lca，两个点都往上跳到lca就行了，于是我们知道确实上升的时候只会走上升边。

可以倍增处理这个跳跃，于是就做完了。复杂度\(O(n\log n)\)。

王卷王说我这太麻烦了，但是实际上它不需要写卡笛尔树，只要正反两遍单调栈就行了。卡笛尔树只是常见的用来描述单调栈结构的方法。

A. Long Distance Coach

居然是可以拒载的（

时间是\(t\)时刻一段的。

看起来我们不能禁止乘客接水，并把水留给司机。

可以把司机的票钱设为正无穷，这样就不需要考虑司机了。

如果一个老哥，他的票钱比他要喝的水还要便宜，那么我们直接把他踹下去算了。这就需要我们权衡一下在何时把他踹下去，因为如果在两个服务站之间没水喝了，我们可以精确控制让他下车，但是同时他后面喝水的人也必须下车，直到下一个服务站。

所以说，如果一个老哥给了很多的票钱，但是前面的老哥喝了很多的水，我们可能会把他俩一块踹下去。我们可以从左往右考虑每个服务站(以及起点)，求出它到下一个服务站之间会有哪些人想要喝水，然后我们只可能踹下去一个后缀。状压dp就可以过subtask1了。

考虑有没有什么牛逼做法。显然dp并不是很有前途，因为最后踹下去的人我们还不知道，甚至还不好猜测有没有性质。能贪吗?

考虑一个经典的基于合并的贪心。我们找到踹下去收益最大的人，把他和他后面的人合并，如果在某一轮他后面没有人，那就把在这一轮踹了他的操作扔进一个序列。对于一个人的集合也是一样的，如果某一轮这个集合的最后一个人后面没有人，那么就把这一轮踹了最后一个人的操作扔进一个序列。如此合并之后，我们遍历那个序列，收益从大到小贪心踹就行了。

但是这还是没有考虑任何细节。一眼就可以看出来这玩意需要合并出指数级的状态数?但是我已经没有任何进一步考虑的能力了。

去看看题解。草，这玩意是dp?

显然dp并不是很有前途。

真有趣（

注意到这么一个事情，打一个比方，假设一个人被踹下去之后，他的灵魂还在车上(只要水不喝水，在没水的时候会下车)，那么他的灵魂不会被踹下去第二次，也就是说他原来的位置会一直有水喝，因为如果我们又想踹他前面的一个人了，那么我们必然是第一次就把他也踹下去，不会留到后面。再或者说，只要一个人被踹了，他前面的人也可以一起被踹。

于是从司机处把环断开，每一脚就会把人划分成两段，两段之间不会互相影响，于是我们看到了一个区间dp，复杂度就是多项式的了。

然后你发现不需要区间dp，因为这是推平若干段之类的问题。直接dp，设\(dp(i)\)表示考虑前\(i\)个人，最多的收益。如果第\(i,i+1\)个人之间有一个服务区，那么我们就可以精确控制把\(i\)和前面若干个人踹下去，于是可以从\(dp(j<i)\)转移过来。于是两个人之间只需要保留最靠前的服务区。这个系数看起来是固定的，但是会乘上前面的人数也就是\(i-j\)之类的，然后你就看到了一个斜率优化，直接做就彳亍了。

B. Long Mansion

好像也尝试过收录在zroi noip18联测，但是也失败了（

考虑类似于病毒传播，如果A可以到B，那么从B出发可以到的房间A都可以到。

然后考虑每个房间能到的都是一个区间。

于是这些房间被划分成了若干个scc，每个scc可以互相到达，而scc之间可以用若干条有向链来描述(从两头指向中间某个点)，也就是每个scc连向左右可以到的第一个scc。然后在这上面就容易统计答案了。

为了找到这些scc，考虑使用类似于病毒传播的boruvka，但是实际上没有必要，只需要开一个连通块然后合并就行了。

然后好像出现了问题，因为你发现我们什么细节都实现不出来。可以考虑直接记搜，据说复杂度是对的，但是不会分析（

看看题解，然后发现很多题解也不会分析复杂度，感觉\(r\)的均摊啥的比较奇怪啊（

官方题解非常复杂。良心deepl/se

考虑一个牛逼想法，如果允许\(n^2\)，我们记搜就行了。

强行缩减状态数，我们只保留每个房间能到的区间，然后对每个房间进行扩展，如果A可以走到B，那么就递归计算B可以走到的，然后把它并入A。如果在这个过程中B又可以走到A了，那么A和B可以走到的区间是一样的，我们用并查集合并A和B。

考虑一个牛逼方法来判断能不能走一步。我们对于每个房间预处理左右第一个可以开它的钥匙在哪个房间，或者也可以理解成对于每个房间求出要往左走，至少需要到达右边的哪里这样的。

现在分析复杂度。考虑一个离奇的事情，每个门只会被左右的房间各穿过一次，剩下的都被记忆化掉了，这显然是对的。于是复杂度就是\(O(n\alpha(n))\)。

呃实际上不需要并查集。我们直接搜，如果产生了环，那么这个更新一定不优，于是我们把它扔掉。复杂度是\(O(n)\)。

但是总感觉哪里不对。想了想你发现，虽然每个门只会被左右的房间各穿过一次，剩下的都被记忆化掉了，但是取记忆化的结果也是有代价的。不过注意到每个记忆化的结果也只会被取一次，因为如果\(i<j<k\)，\(j\)能到\(k\)，\(i\)也能到\(k\)，\(i\)就不会取\(k\)的结果了，在取\(j\)的结果的时候直接就吞过去了。可以用我们刚才说的那个scc来理解这个，scc之间是若干有向链。

如果这里不理解的话，可以去看我新写的讲稿，那个思路比较简明，毕竟这里是记录完整思考过程的。

C. Natural Park

看起来很有趣。

凑一个\(45000\)，它大概是\(1500\times 3\times 10\)，那个\(3\)看起来是常数而\(10\)是\(\log\)。

爆力怎么做?爆力是不是，我们枚举两个点，然后直接判断它俩是否连通。

考虑这个能不能二分，也就是说我们能不能查询\(u\)到某个点集\(S\)有没有边。显然这等价于查询\(u\)能不能到\(S\)中的某个点。

然后这个看起来不行，因为\(u\)可能只能到\(S\)中的一个点。

容易想到一个没啥用的二分。如果我们现在拿着\(u,v\)，那么二分一个最短的点的前缀，只经过这个前缀尝试从\(u\)走到\(v\)，我们可以知道\(u\)到\(v\)点编号意义下最小瓶颈路的瓶颈。

但是这个二分真的没啥用吗?你发现在树上的时候，它求出了\(u\leftrightsquigarrow v\)上编号最大的点，链上则是求了一个区间\(\max\)。虽然我们不知道它和\(u,v\)有没有边。

考虑在链上，如果它不是\(u,v\)中任何一个，那么我们就把这条链分成了两部分。递归下去继续找，我们就可以把这条链找出来，每个点花费是一次二分，于是这就可以用来解决subtask2了。

但是如果它是\(u,v\)中的一个就完蛋了。怎么修补一下让它总是可以求出\(u\leftrightsquigarrow v\)上除了端点的一个点呢?只需要在二分的时候总是允许走\(u,v\)就行了。(也就是说二分的前缀不包含\(u,v\)中若干个的时候还是允许走它们。)

然后链就搞定了。考虑树怎么做，它也是一样的，我们把已经合并的点们看作一个点，然后每次拿一个新点来，找到已经合并的点们和新点之间的链。

但是这个有一个问题，就是比如已经合并的点集是\(S\)，我们现在要加入\(w\)，已经通过二分知道了\(w\)到\(S\)路径上的所有点，但是我们现在不知道\(w\)到\(S\)路径上最后一个点连向\(S\)中的哪个点。

不过这个也好办，我们只需要对这个\(S\)求随便一个遍历序，在上面二分即可。

然后考虑怎么扩展到一般图。考虑最小瓶颈路在最小瓶颈树上(这里是点权，不过可以转边权，也就是边权是端点点权\(\max\))，于是我们直接这么求会求出一个最小瓶颈树。

然后考虑怎么从这棵树构造整个图。你发现比较困难。

考虑修改我们的扩展过程。看起来如果现在有一个\(S\)，问题出在我们要扩展的\(w\)可能与\(S\)有多条边。

只需要多次二分就可以了，总共是\((n+m)\log n\)级别的查询，复杂度则是\(O(nm)\)。好像其实不困难，只是我太拉了（

A. Abduction 2

\(h,w\)都是5e4，时限5s，这说明啥呢/jy

\(q\)只有100，这说明啥呢/jy

于是我们猜测复杂度是\(O(q(h+w))\)。这好像给出了什么方向，但是又好像没给（

这个好像说的是，必须尽可能沿着权值更大的路走。于是它不可能成环了。

此时，

5e4，\(n^2\)冲啊

王卷王之言可谓切中了肯綮。我们可能还有一个\(O(hw/w)\)或者\(O(h\sqrt{h})\)的预处理，当然前面那个\(/w\)指的是bitset除一个字长。

但是这样的预处理怎么说都太过奇怪?呃其实可能也不算奇怪，我们可以搞一个bitset存每个路口往哪拐之类的。

考虑能不能找点性质。

首先我们不可能两次经过一条路。但是答案可以达到\(\Theta(hw)\)，构造是来回走。

然后找不到什么性质了。那就强做，说不定就看出性质了（

考虑权值最大的路，走在它上面就不可能拐弯了，于是走到它上面的时候你可以选择往更长的一边走。

此时考虑与它方向相反的路中权值最大的，走到它上面，你只能在刚才那条路上拐弯。这个拐弯方向一定是朝着那条路更长的一边。

于是一条路会被比它更大的路切成若干段，每一段……没有什么性质。并且总段数是\(O(n^2)\)，所以我们就死了。

那就猜一手，直接记搜是对的，然而这个不太可能（

考虑记搜的时候我们会搜到什么地方。先枚举一个方向，然后走出去之后会遇到一个要拐弯的路口，在这个路口我们往两边搜，然后两边又会遇到路口……

画一画这个过程，你发现一个非常离奇的事情，我们按照权值从小到大扫，每次撞到比当前扫到的权值更大的路时就停下，等到扫到那个权值再决策如何拐。

然后你发现一些牛逼的事情，手玩一下(如果你真的在做这个题，你确实应该画一画)，感觉上我们通过一些剪枝，也就是走到走过的路口就停下之类的，可以保证同一个方向上同时只在搜一条路。此时我们搜过的范围看起来只会扩大\(O(h+w)\)次，此时如果再支持一直跳到下一个路口，复杂度说不定真的对了。

实际上这就是对的。这非常离奇。

然后使用什么数据结构支持查询下一个比这个大的就行了，比如根号预处理\(O(1)\)查询的牛逼根号平衡，也就是先开一个桶找到块，每一块再开一个桶找到答案这样的。

状态数的分析大概是说每个深度都只有最多四个状态，为什么可以去看看官方题解的图，对深度归纳然后胡乱讨论就行了?

好像不用什么离奇根号平衡，直接爆力找速度也很快?

B. city

给一棵树，根是\(0\)，每个点到根不超过\(18\)条边。现在要完成两个程序A和B，A要给每个点分配一个权值，B要支持拿到两个权值(B也只知道这两个权值)，求这两个权值对应的点，哪一个是另一个的祖先，或者它俩没有祖先关系。\(n\leq 2.5\times 10^5\)，点权在\(2^{28}-1\)以内。

这个让我们想起来一个经典题是 ioi2020 网络站点。考虑把括号序压进去。

然后你发现这个也没有做完，因为\(n\)看起来是略小于\(262144=2^18\)这样的，最后我们需要\(2^{36}\)，这好像可以获得22pts。

那么我们怎么才能把括号序压得牛逼一点，以至于砍去一个\(2^8\)呢?显然我们需要用到深度只有\(18\)的性质。

考虑一个牛逼想法，深度只有\(18\)，也就是说一个点的祖先个数很少，于是我们记录一个点的所有祖先。然后因为每个点都记录了所有祖先，所以一个点只需要记录它的父亲。为了保证每个点的权值互不相同，我们就给每个点不同的儿子分配不同的权值就行了，然后这就是一个trie。

然后你发现这个冲不动，因为我们需要区分一下每个数，但是位数很少不能定长编码，于是只能考虑huffman之类的技术，但是huffman又需要通信双方都知道字符集。所以这个可能并没有什么前途。

还是括号序吧。考虑有没有什么牛逼性质。

考虑要记一个括号序，我们可以记两个括号的位置，也可以记第一个括号的位置和子树大小。树只有\(19\)层，于是子树大小之和只有\(19n\)以内，这看起来小的可怜，于是子树大小一共有\(\sqrt{2\cdot 19n}<3083\)种。但是我们好像也没有办法把每种压成一个，因为这还是需要知道字符集。

不管怎么说现在还是有些做掉的可能了。先记发现时间，那么剩下的问题就是用\(10\)位记\(250000\)个和只有\(4750000\)以内的数。然而立刻又感觉这很不可能。失败了。

考虑一个离奇想法，如果这是二叉树怎么做。我们把它填成满二叉树就好了。

这启示我们，可以对树做一些变化，也就是说我们不一定要老老实实记发现时间。考虑我们把每个点的子树大小都变成\(2^k\)，此时就只需要记那个\(k\)了，这就非常牛逼。但是可能我们在做这个的过程中会把点数搞成指数级。此时容易想到利用深度只有\(18\)的性质，我们先尝试毛估估一下这个东西最坏情况下会有多么指数级。

最简单的最坏情况就是每个点都只有一个儿子，子树被填成了\(2^k\)，那么这个点就会被填成\(2^{k+1}\)。这就很不好。

如果每个点都有两个儿子，都被填成了\(2^k\)，这个点就会填成\(2^{k+2}\)。于是看起来最后点数足足有\(2^{36}\)，我们就完蛋了。

那么要怎么办呢?考虑我们把这个子树大小的限制放宽一点，比如要求子树大小是完全平方数。然后我不会分析这个。

注意到这个是一个重构树，于是我们可以考虑用某些离奇重构树来做这个，比如使用类似基于链分治的静态top tree的做法，搞一个huffman树上去进行三度化。然后因为深度本来很小，我们可以想象得到的深度还是很小，然后直接使用二叉树的做法。这能获得多少分呢?不知道，问问vuq。

另一个想法是把这个和之前的子树大小之和很小结合起来。我们可以钦点若干种子树大小，比如\(1,2,3,...,\sqrt{n},2\sqrt{n},...\)这样的。然后这个我也不会分析。

看看题解吧。方法看起来非常强行啊（

我们刚才尝试了\(2^k\)，考虑直接把它扩展到\(\alpha^k\)，其中\(\alpha\)可以有小数，我们取整就行了。发现取\(\alpha=1.05\)的时候就过了，非常离奇。

然后这个为什么是对的呢?考虑如果一个点的高度是\(d\)，那么它的子树大小必然不超过它实际大小的\(\alpha^d\)倍，于是所有点的子树大小都不超过\(\alpha^{18}n\)，于是每一个子树大小需要\(\log_\alpha \alpha^{18}n\)位，于是总位数看起来是\(\alpha^{18}n\log_\alpha \alpha^18n=\alpha^{18}n(18+\log_\alpha n)\)。然后就枚举一个\(\alpha\)就行了，不过我觉得它是单谷的。

geogebra算一下，这个数的精确值是1.0530457308216。

C. Dragon 2

感觉奇怪的计算几何就要写出式子来化一化（

考虑这个式子是啥，你发现射线这个东西很离奇，3e4也很离奇，3s也很离奇。看起来复杂度又是离奇东西，猜四手，分别是\(O((n+q)\sqrt{n}),O(n\sqrt{q}),O(n\sqrt{q}\log q),O(n\log^3 n)\)。

考虑我们从发起攻击的龙往路上画射线，这构成了一个2-side的区域，然而这个区域并不好数点。

试一试把它变换一下。尝试了圆反演，感觉并不行。还有什么想法?

partition tree（

那我们就强硬数点。考虑扫描线怎么扫，我们先把角差分成两个极角的差，然后扫极角。

注意到这个问题中，线段是只有一条的，于是所有的射线都经过线段两端点中的一个，于是就直接分别绕着这两个点转，整个线段树就行了。

然后这个可以做一种颜色和\(q\leq 100\)了。考虑更多的查询怎么做?

呃先强行一下，根号分治，对超过\(\sqrt{n}\)的，我们强行预处理它们和每个颜色的，不到的查了再跑，这就是\(O((n+q)\sqrt{n}\log n)\)了。注意到\(n,q\)并不平衡，所以可以调整一下根号分治的阀值。

常数更小的做法是查询的时候枚举少的颜色，去查多的颜色，并记忆化。

好像突破4w字了（

rnm，终于做完抄完题解了（

joisc还有很多年的，但是据说17是难度顶点了?

loj2729~2740 joisc 2016

这个好像没有英文名（

A. 俄罗斯套娃

感觉上看起来并不困难。横轴是直径，纵轴是高度，那么问题就是查询一个右下2-side区域的最小上升子序列划分，也就是最长不上升子序列。

然后注意到最长不上升子序列的第一项在这个右下区域中，整个就在这个右下区域中，于是考虑dp，设\(dp(i)\)表示结束于\(i\)这个点的最长不上升子序列长度，BiT维护一下这个，然后再对查询扫描线BiT一下就好了。

B. 神经衰弱

看起来比较离奇。我们每次可以获得优先级更小的一个。

考虑subtask2。我们尝试找到\(\max\)。考虑\(\max\)的特点是，只有问两个\(\max\)才能得到\(\max\)。

我们从左往右维护一个\(\max\)。发现如果直接问不知道谁是\(\max\)。

这时候可以考虑爆力一点，两个数我们不能知道谁是\(\max\)，但是如果有三个数，那么三个数中的\(\min\)会在答案中出现两次，于是我们可以排除这个\(\min\)。然后这个看起来不是很对啊，因为如果有两个数都是\(\min\)，那么\(\min\)就会出现三次，我们就没办法了。所以维护四个数就好了，每次插入需要三次新的比较，最后还需要\(O(1)\)次，于是我们用\(6n\)次找到了\(\max\)，问一遍得到答案即可，一共是\(8n\)。

考虑怎么卡一卡，考虑把问一遍的过程省掉，注意到一个数被踢出去的时候，它的值已经得到了，所以就结束了。

B. 回转寿司

注意操作会改变序列\(a\)。

看起来像是类楼房重建线段树，但是类楼房重建线段树打不了这样的标记吧?

数据范围很小，时限巨大，考虑分块。如果查询的是一个整块，注意到答案肯定是\(\max\)，然后\(\max\)会消失掉。所以每一块开一个堆维护\(\max\)，然后跑到零散部分就暴力重构。怎么重构呢?

我们拿到所有的修改，然后在块里从左往右走，如果这个位置不够小，以至于比最小的修改要大，那就拿最小的修改把它换掉，然后它会变成一个新的修改。用一个堆维护\(\min\)即可。复杂度\(O((n+q)\sqrt{n}\log n)\)。

完全不会，我是数据结构垃圾/ll

joisc 2018

C. Tents

看起来非常像是 ahoi2009 中国象棋。

设\(dp(i,j,k)\)表示放了前\(i\)行，有\(j\)列已经有一个没确定朝向的帐篷，\(k\)列已经有至少一个确定朝向的帐篷的方案数，转移的时候，如果这一行放一个帐篷，那就可以放在有没确定朝向的帐篷的列，或者放在没有帐篷的列，可以选择它的朝向；如果放两个，那就会ban掉两个没有帐篷的列，胡乱算一下方案数就行了。复杂度\(O(n^3)\)。

考虑如何优化，看起来我们必须要砍去一个维度。我们枚举有多少列放了两个帐篷，然后剩下的部分就不需要记\(k\)了，然后就组合数选一选就好了。复杂度\(O(n^2)\)。

感觉我做法很正确，但是好像网上做法都不是这样的，是直接在放一个帐篷作为接头的时候，就把前面跟它接上的那一个直接选出来，于是不需要记\(k\)。

qaq

CATALOG

Featured Tags

My Friends(按换友链时间排序)