pam是简单的自动机,它用于计算和索引一个串所有回文子串及它们的结构。pam和border理论可以很好地结合,从而搞出一些看起来很牛逼的题。
比起manacher,pam的优势在于它处理了回文子串的结构。
pam的理论和构造
pam保存了一个字符串中所有的回文子串,其中每个结点都代表着一个回文子串,当然任意两个结点代表的回文子串是不同的。
pam存在的可能性基于这样一个定理 :
定理1 一个串中不同回文子串数量不超过\(n\)。
证明 考虑我们现在加入了一个字符\(c\),要证明不同的回文子串最多增加一个。
考虑如果回文子串增加了,\(c\)肯定和之前的至少一个\(c\)形成了回文子串。考虑设其中最靠前的那个位置为\(k\),那么其它任何一个和新加入的\(c\)形成的回文子串都被包含在和\(k\)形成的那个里面了,所以它们之前一定已经出现过。
感性理解一下,比如有bawabqwqbawa,现在加入了一个b,那么和第一个b形成了回文子串,和第三个b也形成了,但是和第三个形成的那个必然已经在前面出现过了,因为它包含在新加入的b和第一个b形成的回文子串中。
现在我们可以开始考虑pam应该是什么样子的了。
pam匹配的并不是回文子串,因为如果你试一试就会发现那非常困难。pam匹配所有回文子串的半串,半串说的是从回文中心开始的后缀,比如aba的半串是ba,abba也是ba。
首先,作为一个回文数据结构,不可避免的就是讨论奇偶回文的区别。这里我们建立两个根\(-1,0\),分别索引奇偶回文子串。
尽管匹配的是半串,我们还是认为pam的每个点表示一个回文子串,毕竟这样更加直观。我们定义一条转移边是在串的两边同时加入一个字符,fail指针指向一个串的最长回文后缀,也就是存在于pam中的最长后缀。
\(0\)的fail指向\(-1\),而\(-1\)不可能失配,因为它指向的是每个单字符。
要构造pam是简单的。考虑先对于每个点额外维护回文子串的长度\(\mathrm{len}(u)\)。
考虑增量构造。我们先找到以上一个字符结尾的最长回文子串的结点,然后从这里开始往上走fail,不断尝试在前后同时加上现在要加的这个字符,直到某次尝试成功。显然如果之前没有相同的回文子串,我们需要新建结点。
考虑求出新结点的fail。我们只需要再跳一轮fail即可。
复杂度证明是容易的,考虑每轮中以最后一个字符结尾的最长回文子串的点,因为每次跳fail都会减少新加入结点的深度,而挂叶子只会让这个点深度增加\(1\),所以总共就是\(O(n)\)的。
简单应用和扩展
求endpos是简单的,直接线段树合并即可。
回文和border
引理1 回文串\(s\)的前/后缀\(a\)是border,当且仅当\(a\)是回文串。
证明 显然。
由引理1和弱周期引理的某个著名推论,我们可以直接得到推论 : 回文串的所有回文前/后缀构成\(\log\)个值域不交的等差数列。平时能用到的好像只有这个了(
当说一个题用弱周期引理的时候,也可能是用这个推论。
这有什么用?
主要用途是优化 枚举一个位置为结尾的所有回文子串 之类操作的复杂度。
pam可以爆力完成这个工作,而结合弱周期引理可以在1\(\log\)时间内枚举出若干等差数列,如果等差数列在问题中性质足够优秀就会产生巨大的优化。
处理等差数列的一个比较普适的方法是根号分治,但是这个太慢了,所以一般还是要大力寻找问题性质。
最小回文划分
过于经典。给一个串,把它划分成尽可能少的回文串。\(n\leq 5\times 10^5\)。
简单想法是直接暴力dp,在pam上不停跳fail来枚举一个前缀的所有回文后缀。这个是\(O(n^2)\)的。
考虑利用弱周期引理。我们直接把巨量的跳fail变成\(\log\)次,方法是预处理\(\mathrm{diff}(u)\)表示\(\mathrm{len}(u)-\mathrm{len}(\mathrm{fail}(u))\),\(\mathrm{slink}(u)\)表示\(u\)跳fail跳到的第一个不在同一等差数列的点,也就是第一个\(\mathrm{diff}\)和\(u\)不相等的点。当然\(\mathrm{slink}\)算在两个等差数列都可以,我们这里钦定算在下一个。
这要求我们批量处理一个等差数列的转移。考虑设\(g(u)\)表示从\(u\)往上跳,跳到的一整个等差数列的\(\min\)。具体一点,我们假设当前处理到\(i\),这个等差数列是\(aj+b\),那么\(g\)就应该是\(dp(i-b),dp(i-a-b),dp(i-2a-b),...\)的\(\min\)。
如果有了\(g\),求出\(dp\)是简单的,现在主要问题就是每次\(i\)变化之后,\(g\)也在变化,并且变化量还不小,此时我们应该如何搞定新的\(g\)。
简单想法是根号分治之后开一车数据结构硬维护,复杂度是根号\(\log\)。
首先考虑我们只需要改所有等差数列里最长的那个,因为别的都用不到,这样修改量直接变成\(\log\)了。
对于一个遍历到的等差数列中最长的点\(u\),考虑\(\mathrm{fail}(u)\)也就是\(u\)的最长回文后缀,它同时也是\(u\)的最长回文前缀,也就是说它在前面一定对称地出现过一次。
考虑这两次的位置差,你发现它们恰好是\(\mathrm{diff}(u)\),也就是说两个等差数列恰好对应上了,\(g(\mathrm{fail}(u))\)只在右边差了一项。
这里拿一个oi-wiki上的图 :
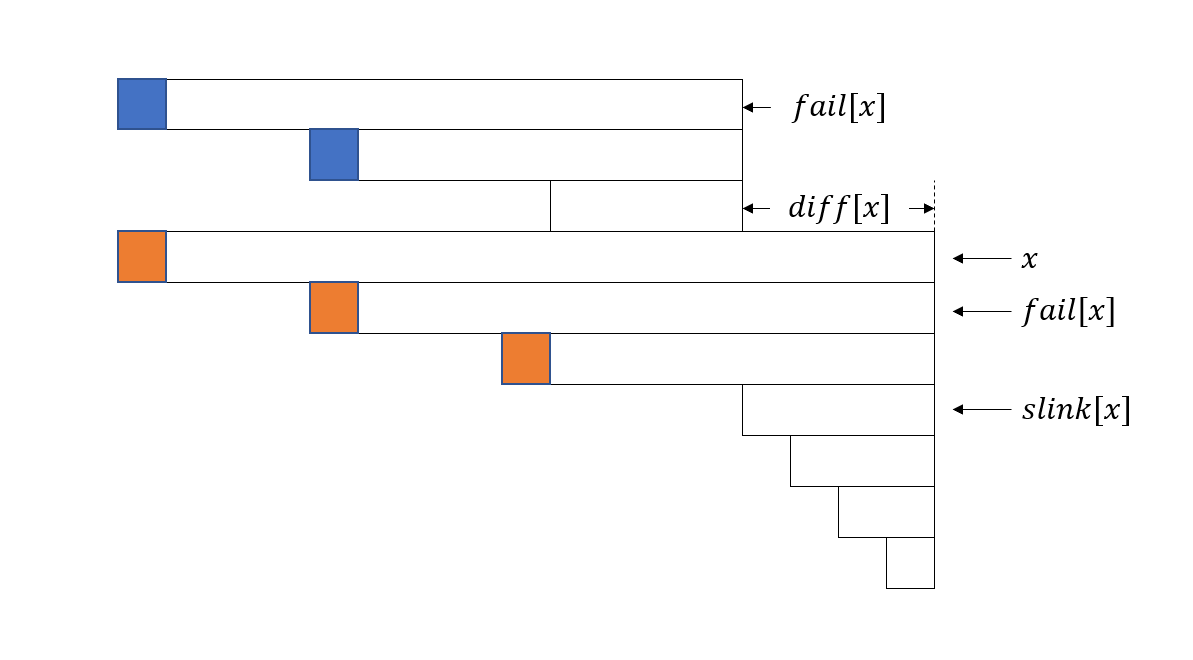
这一项就是\(i-\mathrm{diff}(u)-\mathrm{len}(\mathrm{slink}(u))\)。于是我们就得到了\(g\)的转移。
这就做完了,复杂度是一个\(\log\)。
来注意一点性质
如果你画个图,你会发现,如果现在\(u\)出现了一次,那么\(\mathrm{fail}(u)\)出现两次,\(\mathrm{fail}(\mathrm{fail}(u))\)出现三次,等等,并且每个的出现位置也是等差数列,公差就是\(\mathrm{diff}\)。前提当然是它们在同一个等差数列。
这里我们可以画一张图来理解 :

Gym 102864I shenyunhan Loves Palindrome
定义 循环回文 说的是把一个串复制一倍之后,存在一个长度在\([n,2n-1]\)内的前缀是回文串。给串\(s\),每次给一个区间,求是不是循环回文。\(n,q\leq 2\times 10^5\)。
容易发现循环回文说的是,本身就是回文串,或者可以表示为两个回文串拼起来。
考虑先正着倒着建两个pam+弱周期引理,这样就可以枚举出区间前后缀的所有回文子串。
现在问题是,有两个等差数列的集合,要从中各选一项,使得加起来恰好是\(r-l+1\)。
考虑我们枚举一个,用双指针维护另一个的可能区间,注意这里所有可能区间长度的和确实是1\(\log\)级别,因为等差数列的值域是不交的。
然后我们就需要判断两个等差数列\(ai+b\)和\(cj+d\)是否存在两项加起来是\(k\)。移一下发现变成了\(ai+cj=k-b-d\),所以可以用exgcd解一下,如果存在一组\(i,j\)都在范围内就好极了,否则就见鬼了。
总复杂度是\(O(n\log^2 n)\)。比起最小回文划分,这个题作为例题1.7还是有点逊。
loj6070 「2017 山东一轮集训 Day4」基因/爆炸oj5384 有趣的字符串题
给一个串,每次查询一个区间有多少不同回文子串,强制在线。\(n,q\leq 10^5\)。
爆力就是直接对区间建立pam然后数有多少个点。
另一个爆力是建立全局pam,然后从每个位置出发爆力跳fail,标记确实出现在区间的结点。
这两个有点太爆力了。想点不那么爆力的。
考虑类似于区间数颜色的方法,我们对于每个回文子串,求出来它上一次出现的位置,然后就二维数点了。使用线段树合并来求endpos,复杂度是\(O(n^2\log n)-O(1)\)。
二维数点就很不好,先离线一发,扫描线扫右端点,同时增量建立pam。我们跳fail的时候会跳到一堆已经出现过的回文子串,应该把它们在前面的贡献删去而加到后面来,查询就是区间求和了,这个可以用BiT支持。
先考虑这个爆力怎么做。你发现我们对于一个长\(l\)的回文串,假设它上次出现在\([j,k]\),当前扫到\(i\),那么就相当于把左端点在\([j,i-l]\)的答案都\(-1\)。
利用弱周期引理可以搞出\(\log\)个等差数列,问题是怎么一口气处理一个等差数列。
类似于 最小回文划分,你发现最长的那个上次出现位置可能很奇怪,但是等差数列中更短的串,上次出现位置已经确定了,它们的endpos全都是\(p=i-\mathrm{diff}(u)\)。
然后你发现,\(\mathrm{fail}(u),\mathrm{fail}(\mathrm{fail}(u)),...\)做的区间\(-1\)顺次接起来了,最后我们得到一个\([i-\mathrm{len}(u)+1,i-\mathrm{len}(\mathrm{slink}(u))]\)之类的东西。
这里还是需要那个图来理解一下。

hdu6791 Tokitsukaze, CSL and Palindrome Game
定义一个串的权值是不停掷骰子第一次搞出它来的期望次数。给一个串\(s\),每次给两个回文子串,求哪个权值更小。\(n,q\leq 10^5\)。
实际上我们好像可以直接求出这个权值(
考虑这是经典的掷骰子问题,我们去翻一翻pgf是什么,然后就可以设这个子串长度是\(l\),答案的pgf是\(F\),没搞出来的pgf是\(G\),然后就有
-
如果加了一个字符,要么搞出来了,要么没搞出来
-
如果直接加上整个子串,一定可以搞出来,此时如果在第\(k\)个字符处已经搞出来了,要求\(k\)是一个border,并且前面\(l-k\)个恰好是我们要的。
,然后就可以得到
\[\begin{aligned} zG+1&=F+G\\ \frac{1}{\Sigma^l}z^lG(z)&=\sum_{i=1}^l[i\text{ is a border}]\frac{1}{\Sigma^{l-i}}z^{l-i}F(z) \end{aligned}\]。给第一个对\(z\)求导,我们得到\(F^\prime(1)=G(1)\),再看第二个,可以得到
\[G(1)=\Sigma^l\sum_{i=1}^l[i\text{ is a border}]\frac{1}{\Sigma^{l-i}}F(1)\],注意到\(F(1)=1\),所以
\[G(1)=\sum_{i=1}^l[i\text{ is a border}]\Sigma^i\]于是我们就考虑怎么算这个。显然是利用pam+弱周期引理枚举所有的border,那么如何一口气处理一整个等差数列?
注意到权值非常大,不过每个长度的border最多只有一个,所以这个加法放在\(\Sigma\)进制下不会产生进位,所以我们比较字典序就行了。比两个等差数列显然是简单的。
存在不使用border理论的做法,比如用树上倍增+hash来比。
loj6681 yww 与树上的回文串
给一个树,边有字符,求有多少路径上的字符串起来是回文串。\(n\leq 5\times 10^4\)。
考虑点分治。当然这里需要容斥,不过我们先不考虑那个。
考虑一个回文串会分成三段ABA',其中B和A'之间是分治中心,A'是A的翻转,B是一个回文串。
考虑我们数据结构搞定A',然后枚举AB,这么做是因为B是AB的一个回文后缀,而所有回文后缀都是最长回文后缀的border,根据弱周期引理可以划分成\(\log\)个等差数列。
如何求出这些等差数列?你发现我们是向前加字符,撤销,查询回文后缀们构成的等差数列,所以我们实际上只需要维护最长回文后缀和所有等差数列,这个可以容易地hash一发,配合可撤销化数组搞定。
现在问题是如何一口气求一个等差数列的前缀的出现次数。考虑最爆力的技巧,我们对公差根号分治,超过根号的部分查询不超过根号次可以爆力hash;根号以内的可以离线下来对每个公差\(k\)这么处理,我们按照膜\(k\)跑\(\frac{n}{k}\)遍,每一遍用一个扫描线+hash table搞定。做完了,复杂度根号\(\log\)。
当然这个还是太慢了,根本跑不动,要优化就需要抛弃性质较差的hash,这里我们改用acam。对所有A'建立acam(实际上就是在原树上自底向上合并每个点所有子树得到一个trie,然后跑acam),那么一个等差数列匹配的次数就是从最长的那一项开始不停往上跳公差直到最短的一项,给走过所有点求个和。
还是根号分治。公差超过根号的部分只要跳不超过根号次可以爆力。注意到即使考虑所有\(\log\)个等差数列,公差超过根号也只能跳根号次,所以这部分实在是一个根号。
根号以内的部分还是直接按照膜\(k\)跑树上前缀和,这里空间巨大也需要离线。
点分治不会多\(\log\),因为每层是高于\(\tilde{O}(n)\)的。总复杂度是一个根号。