AGC选㗅

远古ARC(058~103)做完了，咕咕咕结束了，原坑 AGC数数题，但是反正要刷穿不如直接全做了。

打开AGC，从上往下做。简单题可能略过。

考虑了一下，题选做 这个tag的含义可能是记录我思考的过程，也就是一边做题一边写的笔记之类的。

这个咕了。新的atc选做在很后面。

AGC001B : 你发现这是一个类似于辗转相除的过程，所以就除就行了。存在直接用gcd算答案的方法，不过我不会推。

AGC001C : 看起来好像有点好玩。首先直径上的点是一定要被删的，但是我们删哪一边呢?

不知道，但是我们可以连一条边表示两个点不共存。所以做法就是直接求出到一个点距离\(>k\)的点，爆力连边然后跑最大独立集。

最大独立集显然不行，如何优化?

这个是不是二分图?看起来不是。

这个有啥性质?你发现没有传递性，那还能有啥呢/yun

补图?最大独立集可以转为补图最大团，然后补图就是每个点连到一个邻域，这个有啥性质啊……算了吧，换个想法。

直径总是跟center相关，我们可以枚举一个center，然后保留到它距离不超过\(\frac{k}{2}\)的点，做完了。笑死我了。

AGC001D : 考虑那个回文的条件说的是什么。我不知道（

考虑实际上说的就是我们根据这些回文的条件可以获得一组全部相等的条件，而回文的条件就是若干个 某两个字符相同。

考虑一个简单想法(反正我没想到)，你发现一个回文串和它shift一位拼起来会发生好玩的事情，比如说我知道\([1,4]\)是回文，知道\([2,5]\)是回文，那么就有\(1=4=3=2=5\)。所以说我们可以构造一个，\(b\)的第一项是\(a\)的第一项\(-1\)，最后一项则是\(+1\)，中间是一样的。

诶我们还没考虑奇回文。如果\([1,5],[2,6]\)是回文，那就有\(1=5=3\)，诶推不动了/yun

这是为什么?从本质上来说，一共有六个数，但是长为五的回文串只确定两个等价关系，所以一共只有四个等价关系，连不起来。

那么也就是说奇数必须跟偶数贴在一起，比如\([1,5],[1,4]\)是回文，那就有\(5=1=4=2=3\)，\(5\)是可以和后面接起来的。所以如果奇数不超过两个，我们就把一个奇数放在最前面，另一个奇数(或者某个偶数)放在最后面，然后按照上面的方法构造即可。

AGC001E : 来好玩的了。数数题，虽然不够数数。

先变成有序对并且可以相同，最后减去自己和自己再除一个\(2\)即可。

你发现值域很小，直觉是复杂度是\(O(n\log n+v^2)\)。

考虑那个式子是什么，它就是\(\frac{(a_i+a_j+b_i+b_j)!}{(a_i+a_j)!(b_i+b_j)!}\)，所以我们枚举\(a_i+a_j\)和\(b_i+b_j\)，目标就变成算有多少对满足\(a_i+a_j=x,b_i+b_j=y\)。这个看起来也很困难/jk

算多少对满足\(a_i+a_j=x\)是简单的，只需要法法塔就好了。这样的话这个就是二维卷积，虽然可以转化成普通卷积，但是4e6的范围还是受不太了。

还是来点神仙做法吧。考虑怎么分离\(i,j\)，可以使用范德蒙德卷积，看起来更好的方法是使用它的一个对称的变形\(\binom{a+b}{c+d}=\sum\limits_{i=0}^k\binom{a}{c+i}\binom{b}{d-i}\)，于是我们得到

那么问题变成怎么对\(k\)从\(-v\)到\(v\)，求\(f(k)=\sum_{i=1}^n\binom{a_i+b_i}{a_i+k}\)。

考虑\(a_i+b_i\)和\(a_i+k\)都很小，于是我们考虑每个\(i\)对哪些\(f\)有怎样的贡献。容易发现每个\(i\)的贡献从\(b_i\)开始，可以认为一直延伸到无穷处(因为正的下指标不需要边界，但是负的需要)。

为了使用OGF，我们先给\(f\) shift \(v\)位，这样就避免负的下标了。

考虑\(\binom{a_i+b_i}{a_i+k}\)在\(k=-a_i,-a_i+1,...\)处的值的OGF(当然也shift \(v\)位)，它就是\(z^{v-a_i}(1+z)^{a_i+b_i}\)，所以答案的OGF即为

。注意到乘\((1+z)^{a_i+b_i}\)是容易的，所以我们枚举\(a_i+b_i\)，此时对应的所有\(z^{v-a_i}\)加起来得到一个多项式(这也是为什么我们不枚举\(v-a_i\)，因为\((1+z)^k\)们加起来得到的多项式不容易快速计算)，可以爆力求出它在\(0,...,2v\)的点值，然后爆力卷上\((1+z)^{a_i+b_i}\)加入答案即可。

啊你问怎么卷?卷\(1+z\)就是前缀和，卷\((1+z)^k\)就是\(k\)阶前缀和，直接组合数算出每个数被前面每个数贡献多少次，然后拆一下递推即可。

另一个做法是这个式子具有非常明确的组合意义，也就是从\((0,0)\)走到\((a_i+a_j,b_i+b_j)\)的方案数。注意到它等价于从\((-a_i,-b_i)\)走到\((a_j,b_j)\)的方案数，所以我们就完成了分离，并且可以用一个dp直接统计答案。

AGC001F : 好复杂。

先看看逆排列上这个操作是否有更加简单的形式，你发现它变成了，对于两个相邻的数，如果差至少是\(k\)就可以交换。看起来确实更简单了?

考虑此时最小化字典序变成了什么。最小化第一位，等价于最小化逆排列的\(1\)的位置。

所以我们要尽可能把\(1\)往前换。如果换着换着遇到了一个\(k\)以内的数，也就是不能和\(1\)换的数，那么我们只能尝试把这个数往前换，尽可能换到靠前的位置再回来处理\(1\)，这样贪心的正确性在于操作可逆。

注意到这个过程中可能进行一共\(n^2\)次交换，所以我们需要一个数据结构来维护交换的过程，平衡树即可。然而也不需要平衡树，请见 https://www.luogu.com.cn/blog/lingfoxchong/solution-at1984 。

存在进一步转化的更简单做法。考虑如果满足 不能换的都没换 这个限制，就一定合法，而不能换的就是差\(\leq k\)的。所以我们给差\(\leq k\)的对，小的向大的连有向边，表示顺序，然后问题变成求一个拓扑序，先最小化\(1\)的位置，再最小化\(2\)的位置……

这个看起来好复杂啊，考虑一个递推，我们设\(dp(i)\)表示\(i\)最小出现在哪，那么实际上\(dp(i)=1+\max\limits_{j\rightarrow i}\)，可以用线段树维护。不过这是错的，因为我们需要把别的点也插进来/jy

这条路看起来不是很能走通，不过我们可以换个方向。注意到最小字典序拓扑序是容易的，于是我们考虑把图从逆排列转化回原排列，也就是对图的编号取逆排列得到原排列，这样问题就变成最小字典序拓扑序了。

吗?没有，想一想你发现并不能这么做。

考虑一个普及组贪心想法，这等价于最大化这个拓扑序反过来的字典序。感性理解一下，这个正确性在于，我们需要尽可能把大的放在后面，这样它们就不会把小的憋在后面。

所以我们只需要取反图，然后就变成最小字典序拓扑序了。用线段树支持找出所有\(0\)并赋为inf，这里全是正的所以维护最小值即可；堆支持查询最大的点。

AGC002C : 想了五分钟，发现时间倒流就做完了。

AGC002D : 二分一波，然后就变成可以走到Kru重构树上的两棵子树，这个可以倍增搞掉。可以走到的点数就看两棵子树是不交还是包含来算即可。

可以把二分换成倍增砍去一个\(\log\)。

AGC002E : 注意题意是吃最后一个糖的人输了。不过实际上没啥区别（

考虑从大到小排序，那么操作一就是砍去左边，操作二就是砍所有的，你发现如果看成平面上的一排柱子，第\(i\)个高度是\(a_i\)，那么就好像可以选择把\(x,y\)轴向右/上移动，谁移了一步恰好把整个图形移出第一象限，谁就赢了。

考虑两轴的交点，你发现等价于可以把这个交点向右/上移动，移到边界上就输了。

考虑这个点在不同的地方的胜负情况。第一层(最外一层)当然是先手必胜，然后第二层所有向外凸出的拐角处的那些点是先手必败的，因为只能转移到先手必胜的位置。这些点左边和下边是先手必胜的，依此类推。

画一画，你发现两个性质 :

• 一个位于第二层点的胜负只和它到右/上边界距离的奇偶性相关

• 一个位于第二层的点的胜负和它左下方一条线上所有点的胜负相同

。第二个的证明是容易的，假如它是先手必败的，那么它左边和下边是先手必胜的，那么它左下就是先手必败的。假如它是先手必胜的，意味着它左边或者上边是先手必败的，那么这个先手必败的左下方都是先手必败，所以这个先手必胜左下方也都是先手必胜。

所以我们只需要考虑\((0,0)\)右上方位于第二层那个点，到右/上边界距离的奇偶性。排序扫即可。

存在线性做法。考虑即使没有排序，只要找到了那个点在哪一列，到右/上边界的距离都是可以简单地线性完成的，所以问题是找那一列，也就是\(\mathrm{rank}(a_i)+1>\mathrm{suc}(a_i)\)的第一列，这里的\(\mathrm{rank}\)是从大到小排的，\(\mathrm{suc}(a_i)\)是序列中不比\(a_i\)大的最小的数。当然为了避免数值相同，我们一律以下标为第二关键字即可。

二分这个\(i\)的\(\mathrm{rank}\)，使用nth_element求出它的\(\mathrm{suc}\)也就是\(\mathrm{kth}(mid+1)\)，然后判断即可。nth_element会自动帮我们进行划分，再求的时候容易减半，于是复杂度是线性。更好的方法是直接把这个二分和nth_element的划分过程结合起来，这需要自己实现一个，但是它并不复杂只是比较麻烦。我不理解严格线性kth，不知道它能否这样使用。

AGC002F : 真正的AGC数数题，终于见面了（

如果没有染白大家都会算!

如果有染白，一种最终的序列就可以对应多种排列了。如何去重?

先考虑两个排列什么时候会算重。如果它们除了最后被染白的部分都相同，只有染白了的部分做了某些交换，那就会算重交换的方案次。注意到这个方案是难以计算的，所以这条路走不通。

考虑判定什么样的序列是可以搞出来的。容易发现这是一个类似括号匹配的过程，它要求每个颜色的球第一次出现的时候，前面都有充足的白球作为这个颜色失去的真正的第一次出现。

那么我们给每种颜色第一次出现赋权值\(-1\)，白球赋权值\(1\)，问题变成所有的前缀和都为正。容易想到一个dp，设\(dp(i,j,k)\)表示填了\(i\)个位置，已经有\(j\)个颜色出现了一次……你发现转移需要记这些颜色分别还剩多少球，因为题目要求每种颜色恰好\(k-1\)个。这个也行不通了。

换个决策顺序，我们每次往序列里填一个颜色的所有\(k-1\)个球。设\(dp(i,j)\)表示已经填了\(i\)个白球和\(j\)个别的颜色的球的方案数，那么每次可以选择 :

• 填一个白球，这会使得……草?你发现这需要记一车东西，所以我们并不能这么决策。考虑一些别的决策方法。

考虑左边第一个空位放什么。如果放白球，那么啥事没有；如果放别的颜色的球，我们就组合数选出剩下的位置即可。有\(dp(i,j)=dp(i-1,j)+\binom{nk-i-(j-1)(k-1)-1}{j-2}dp(i,j-1)\)。

AGC003B : 容易想到网络流，但是这个题的限制并不能用网络流表述。

考虑了一下神仙做法线性规划对偶定理，发现不行。

那还是老老实实贪心吧（

考虑硬贪，我们先把每个自己跟自己搞到\(2\)以内，然后从左往右直接进行相邻的配对。注意到这样可能出小问题(但是样例卡不掉，毒瘤出题人)，也就是像1 2 1这样的会被搞成1 0 1你就没了。所以我们需要还是从左往右扫，不过先贪心和上一位匹配，再膜\(2\)。

AGC003C : 草?

你发现这跟ARC102F几乎一致，这个操作2的性质就是它可以给奇数位置排序，偶数位置排序，但是并不能交换奇数和偶数位置。排好之后算逆序对即可。

呃好像不是。考虑每次操作1可以把一个奇数搞到偶数位，一个偶数搞到奇数位，那么我们先用若干次操作1换这些，剩下的可以直接用操作2排，这就对了。

AGC003D : 如果分解了就好说了，我们只需要次数膜\(3\)分成若干等价类，然后\(3\)进制\(\mathrm{xor}\)意义下相反的等价类不能共存，取大小更大的即可。

但是全分解是困难的。考虑我们先给每个质因子次数膜一个\(3\)，这个复杂度是\(O(n\sqrt[3]{n}/\log n)\)，还挺快。然后直接分等价类，问题是怎么找相反的。

不会找/yun，我们再分解一下吧。拿\(\sqrt[3]{v}\)以内的质数进行分解，复杂度还是\(O(n\sqrt[3]{n}/\log n)\)，接下来每个数还剩不超过两个质因子没有被找到。考虑我们如果把数分成剩下\(1,p,pq,p^2\)的四类，那么\(pq\)那一类必然没有贡献，\(p\)可能和\(p^2\)配对，\(1\)内部可能配对。第一类可以用MR和开根搞定，第二类已经分解完了可以直接找。做完了。

AGC003E : 可 持 久 化 平 衡 树

注意到数组长度可以缩小，而如果不考虑缩小的话……问题也很复杂。fuck。

不管怎么样还是考虑避免缩小吧。先增大后缩小的话，显然等价于直接增大到缩小后的长度，所以用栈筛去无用的增大，也就是后面被缩掉了的增大即可。

然后问题变得简单起来。考虑我们每次加入的部分是什么，你发现我们可以递归下去，问题会变成查询每次操作之前的整个串和一个前缀每个字符的出现次数。

整个串就是我们要求的东西，问题是怎么把一个前缀做掉。你发现一个前缀会变成若干个之前的整个串和之前的一个前缀，这个影响还是取膜，所以每层会增加一个查询。

注意到取膜具有非常好的性质 : 如果膜掉了，被膜的数至少减半。所以每个前缀的查询只会被膜\(\log\)次，所以我们可以通过某种方法，比如线段树找到所有这样的查询爆力给它们膜。这部分是俩\(\log\)，可以使用高效堆做到一个\(\log\)。

然后问题是怎么往上推，我们只需要把这个过程倒过来就好了。

一个更好写的做法是，我们根本不需要倒过来，只需要把贡献一起扔下去。可以想象最后得到若干个前缀加(呃大概是?)，差分-前缀和即可。

AGC003F : 考虑两个一级分形拼起来会发生什么事情。

优质解答 : 我不知道 考虑如果只有一条横线会发生什么。你发现只有左边和右边都是黑色，接起来才可能减少连通块数。

考虑对于一般的图，我们计算一级分形横着重复两次会少几个连通块(也就是比起一级分形连通块数的两倍少多少)，记为\(c_1\)，竖着类似计算\(c_2\)。记一级分形黑格数为\(t\)。

注意到题目保证了一级分形的连通性，这说明\(c_1,c_2\)都只可能是\(0,1\)，并且给出了两个特殊情况 : \(c_1=c_2=0\)，此时答案就是\(t^{k-1}\)；\(c_1=c_2=1\)，此时答案就是\(1\)。

于是我们只需要考虑横着连起来减少的连通块，也就是\(c_1=1,c_2=0\)的情况，竖着连起来是一样的。问题看起来简单多了。

考虑一级分形横着重复三次会减少多少个连通块，你发现实在就是\(2\)。也就是说有多少对横向相邻的黑格，就减去多少，也就是说最后的答案就是把每个一级分形看成一个黑格之后，\(t^{k-1}\)减去横向相邻的黑格的对数。

两个分形横着拼起来会增加一些横向相邻的黑格，也只有这种方式会增加横向相邻的黑格。

我们求出两个一级分形横着拼起来增加的对数\(r_1\)(实际上这个强转bool等于\(s_1\))，设一级分形里面横向相邻黑格的对数是\(s_1\)，那么容易知道\(s_2=ts_1+s_1r_1\)，同时容易知道\(s_n=ts_{n-1}+s_1r_{n-1},r_n=r_1^n\)。矩阵快速幂即可。

AGC004A : 尝试从每一维中间切开。

AGC004B : 考虑我们可以在shift的时候在不同的时刻加入那些要shift不同次数的，所以枚举shift多少次，问题变成若干个区间\(\min\)加起来。单调队列就做完了。

AGC004C : 正叔给了一个不依赖边界为空性质的，但是那个太复杂，考虑我们奇数行在第一个涂黑，偶数行在第二个涂黑，第一个涂黑左边，第二个涂黑右边，这样就赢麻了。

AGC004D : 内向基环树。

考虑解的结构。如果\(1\)不在环上，那就没救了。如果环长度不是\(1\)，那也没救了，因为环转一圈还是环。于是我们知道，环必然是\(1\)的自环，并且树的高度不超过\(k\)。

现在如果\(1\)在环上，我们把\(1\)连向自己，直接得到一棵树，于是可以直接做。

怎么直接做?问题相当于我们要选若干个点连到\(1\)，要求深度足够小，于是可以直接能不连就不连来贪心。

AGC004E : 看起来比较复杂/jk

考虑这个东西只跟两维上移动距离的最大值和最小值有关，所以我们枚举这四个值，就得到一个\(O(n^5)\)做法。

考虑优化，你发现我们不一定非要\(O(n)\)判，可以用前缀和预处理然后\(O(1)\)判，所以你就\(O(n^4)\)了，注意空间不大需要开short。极限过题?实际上并没有，还挺快的。

AGC004F : 看起来非常简单，但完全不简单/jk

首先奇数肯定无解，因为这个操作不改变异或和。

考虑树怎么做，是不是我们随便取一个根，然后自底向上做。一个点可能有些儿子没有被搞成白的，那么我们就先操作一个儿子和它……遇到了僵局。

考虑这个操作是操作相邻的一对，于是我们黑白染色。这个对于偶环树是可行的，但是奇环树是不行的，不过我们先不管这些，毕竟可以先猜一个奇环树压根不行（

我们用一个经典的网络流trick，认为黑点一开始都是黑的，白点一开始都是白的，目标是把白点变成黑的，黑点变成白的，每次操作就变成了交换两个相邻的点的颜色。这个的好处是去掉了相同才能操作的限制。

所以我们知道，如果黑白点个数不相等，那就无解了。除此之外猜测一定有解。

树的话，考虑还是自底向上做，假设一个点是黑点，那么儿子都是白点。现在有一些儿子是白色的，那么就需要把它们换上来，然后留下一个，剩下的换给父亲往上走。当然也可能出现子树里有些黑点不是黑的，那我们就把一棵子树多出来的换到另一棵子树里。所以最后答案就是每个点子树内黑白点个数差之和，因为你一定要换这么多次换出子树或者换入子树。

偶环树的话，考虑这是一个环上的移动问题，可能有人见过，这是 均分纸牌 的环版本。结论很经典，我们这里来推导一下。

考虑我们只需要随便断一条边，枚举上面有多少黑色过去就好了，当然这个次数可以是负的表示反向通过。由于最优解上这条边一定有一个通过的量，所以随便断一条是正确的。

序列的均分纸牌是容易的，因为我们从一边开始做，就只有不得不换了。最终答案是每一个点子树内黑白点个数差之和。

考虑总代价，假设这些子树内黑白点个数差分别是\(a_1,...,a_k\)，你在\(1,n\)之间移动了\(x\)个，那么贡献会是

你发现这好像是说，我们求前缀和，然后只考虑前\(k-1\)项，那么贡献是\(x\)在数轴上到这些点的距离和(再加上最后一项，不过它是\(0\)所以没关系)，易知取中位数最优。

那么问题是如何证明奇环树无解。你画了一个奇环树，发现它有解/fad

如果对奇环树也黑白染色，环上会有一条边端点同色。你发现如果我们对这条边操作，效果会变成如果它们同色，同时改变这两个点的颜色，不同色则不能操作，于是我们可以用这个来改变黑白色的数量，如果黑白之差是偶数就可以这么调。同时它没有交换的作用，于是我们也不用破环成链了，直接按照树做就好了。

题解的偶环树做法好像和我略有不同，不过没什么关系，我相信我的正确性，虽然我没写。

AGC005A : 中文题面搞什么（

用栈维护串即可。

AGC005B : 考虑每个数的贡献，是一个矩形，单调栈即可。

AGC005C : 考虑最大的一定是直径端点，这个值是直径长度，最小的一定是center(只有一个)或者center所在边的端点(有两个)。

考虑如果直径唯一，也就是直径端点只有两个，那么我们把直径搞出来，所有的贡献一定在直径上取到，而直径上的\(a\)值就是从center出发递增。

如果我们可以搞出直径，剩下的点就一定可以了，因为它们总能挂在直径上某一个位置。判断是否足以搞出直径即可。

AGC005D : 这种排列计数看起来很不可做/fad

容斥一波，然后钦定若干个位置满足\(p_i=i\pm k\)，剩下的随便排了。

现在问题是有多少种方法选出这些被钦定的\(p_i\)，因为\(i\pm k\)们可能是会重复的。

给下标按照膜\(2k\)分组，那么每组相邻的两项都钦定了就会重复，而组之间是独立的。

对于每一组分开dp，设\(dp(i,j,0/1)\)表示考虑前\(i\)个，钦定了\(j\)个，第\(i-1\)个没有/有钦定的方案数，最后把所有的\(dp\)卷起来(分治的话复杂度应该很对)，就得到全局选出被钦定的\(p_i\)的方案数。做完了。

看起来非常正确，但是跟题解做法好像不太一样/ll

AGC005E : 感觉思维难度远高于F/jy

考虑什么情况下会永远进行，如果一条红边的端点在蓝树上距离至少是\(3\)，那么当Bob冲过来的时候，Alice只要反复横跳就好了。

如果没有这种情况，每条红边要么和蓝边重合，要么和两条蓝边构成一个三角形。

这说明什么?如果Bob想把Alice摁在一棵蓝子树里，Alice不管怎么借助红边跑，Bob都可以向上一步截住Alice，所以Bob就可以把Alice摁死。

现在Alice只能选择往哪棵子树走了。以Bob的起点为根把树拎起来，那么Alice先尽可能向上走，然后如果可以走到一个 无 限 之 环 那就冲过去，否则走向最深的儿子即可。

足够厉害/fad

AGC005F : 不得不想到法法塔（

为了叙述简便，定义一个选点方案的权值是包含它的最小连通块大小，也就是它的斯坦呐树大小。

考虑简单dp，设\(dp(u,i)\)表示在\(u\)子树里选了\(i\)个点，并且强制选\(u\)的所有方案权值之和，那么合并两棵子树就是笛卡尔积，但是这里不是乘而是加!

怎么办呢，我们可以取一个\(\exp\)，然后就做完了。

吗?2e5可还行，不过这里是卷积，我们可以考虑优化。

然而这是树卷积，好像很难优化/cy

考虑换个做法，我们统计每个点在多少种方案里，这个用\(2^n\)减去只选在每个子树里的方案数之和即可。

然而这里有一个点数，导致复杂度还是很高，写个式子?

这个能否法法塔?化一下 :

考虑设\(c_i\)为\(s_j=i\)的\(j\)个数，那么就变成

忽略\(k!\)，即为差卷积。

注意这题要呐塔塔的话，据说原根是\(5\)。

AGC006B : 看到中位数，想到转01，于是问题变成有若干-1,0,1，要求最后剩下一个0。

然后呢?考虑一个非常扯的事情，我们只要填一发-1,0,1，就可以保证最上面得到0，因为这样一来左边永远\(\leq 0\)，右边永远\(\geq 0\)。

AGC006C : 非常经典。对称点是线性的，根据期望的线性性，我们可以把它拆开，于是就变成一类cf上做奇怪操作的题，差分一下就做完了。

AGC006D : 经典再现。二分转01，然后连续段会一步一步侵蚀交替段，看哪个连续段离的最近即可。这个比那个经典题要弱?

呃考虑如果有两个不同色的连续段离的一样近怎么办，你发现这就没救了，但是这种情况不可能出现，因为中间交替段长度也是奇数。

AGC006E : 看起来好鬼。

注意到操作是隔一个的，于是还是对列黑白染色。如果出现把黑色换到白色，那就是不可能的。

每一列是什么不会变，只会变上下的顺序，所以如果一列里的数不对就没救了。把每一列压成一个数，那么可以认为这个操作是把相邻三列取负，并交换两边的位置。

现在问题变成，有一个带符号的排列，每次可以把相邻三个数取负，并交换两边，问能不能排序，并且排完序是全正的。

考虑还是拿必要凑充分。交换两边是经典的，如果只考虑黑色，那么每次要么减少一对逆序对，要么增加一对，并且会给白色的符号取反。所以一个必要条件是，逆序对数的奇偶性和白色的符号对应。猜测这是充要的。

写了一发你发现过了。感觉这个题完全弱于ARC102F。

AGC006F : 看起来更鬼了。

你发现这个像是某种 两个维度之间的传递性，听起来很离谱。

如果我们把两个维度拍成一个维度，也就是说经典的建图是建两排点，现在我们建一排点，而把\((x,y)\)看成\(x\rightarrow y\)的有向边，那么这个就变得好像很简单了。

考虑一个弱连通块怎么做。这个非常神。

看到有向图三元环，想到三染色。我们要求每条边都是\(\mathrm{R}\rightarrow\mathrm{G},\mathrm{G}\rightarrow\mathrm{B},\mathrm{B}\rightarrow\mathrm{R}\)之一，那么如果可以这么染色，就可以把所有剩下的\(\mathrm{R}\rightarrow\mathrm{G},\mathrm{G}\rightarrow\mathrm{B},\mathrm{B}\rightarrow\mathrm{R}\)这样的边加进去。

如果不能这么染色呢?考虑如果点\(u\)被同时搞了两种颜色，那么\(u\)就可以自己连自己了，于是它又被搞第三种颜色，于是剩下的点不管是什么颜色都可以和\(u\)连边，这样每个点都可以是任意颜色，于是必然可以连成完全图。

做完了。足够厉害。

AGC007A : 挑 战 哈 密 顿

搜就是了（

诶，好像可以直接走的啊（

AGC007B : 有点意思。

考虑先全凑成相等的，然后依次加上\(\epsilon,2\epsilon,...\)这样的，值域很大所以不慌。

AGC007C : 足够厉害。

首先注意到一个事情 : 球和洞是等价的。问题实际上可以变成，有\(2n+1\)个点，距离是等差数列，每次选相邻两个删掉。

结论是，每次操作之后，剩下的球和洞的位置期望还是等差数列，证明方法就是大力算出每个\(d\)的期望。由于期望的线性性，我们只需依此迭代\(n\)轮。

那么怎么算这个等差数列呢?如果我们已经证明了结论，那么期望已经都算好了，否则我们只需要算第一项和第二项。还是猜结论比较刺激，我们设原来的\(d\)为\(ai+b\)，新的\(d\)的期望为\(d^\prime\)或者说\(a^\prime x+b^\prime\)。

• 如果操作了第一个点和第二个点，那么\(d^\prime_1=d_3,d^\prime_2=d_4\)

• 如果操作了第二个点和第三个点，那么\(d^\prime_1=d_1+d_2+d_3,d^\prime_2=d_4\)

• 如果操作了第三个点和第四个点，那么\(d^\prime_1=d_1,d^\prime_2=d_2+d_3+d_4\)

• 如果不是上面三种情况，什么事都不会发生

，上面三个的概率都是\(\frac{1}{2n}\)，最后一个是\(\frac{2n-3}{2n}\)。综合起来，我们得到

\(d^\prime_1=\frac{(2n-1)d_1+d_2+2d_3}{2n},d^\prime_2=\frac{(2n-2)d_2+d_3+3d_4}{2n}\)，然后代进去那个等差数列就有\(a^\prime+b^\prime=\frac{(2n+7)a+(2n+2)b}{2n},2a^\prime+b^\prime=\frac{(4n+11)a+(2n+2)b}{2n}\)，解就是了。最后得到\(a^\prime=\frac{(2n+4)a}{2n},b^\prime=\frac{3a+(2n+2)b}{2n}\)。

然后如果拿着\(a,b\)要求期望长度的话，是不是是个人都会求啊（

这个让人不得不想起 斗主地。

实际上证明结论也是简单的，只需要像刚才那样讨论一下就好了。

AGC007D : 你发现这个过程肯定是，我们冲到某个点，然后回去一直走到第一个还没拿的钱，在那里等到它可以拿，然后冲回去继续往前(，这个过程中就会把这一段所有都拿走，因为一个可以拿了，走到后面就都顺着拿掉了)。

所以我们以这个回头的点为阶段划分状态，设\(dp(i)\)表示拿了\(i\)和之前的所有点，现在在\(i\)，\(i\)之后的点还没碰的最小代价。转移就是枚举上一段的结尾，复杂度\(O(n^2)\)。

如何优化?爆力做法是线段树，不爆力做法是考虑式子。

\(x_i-x_j\)这一项是没有用的，因为最后加起来总是\(x_n\)。考虑那个\(\max\)，它在一个前缀取到前一项，于是我们双指针扫那个分界点，后面用单调队列维护，前面直接记一个\(\min\)即可。复杂度是线性的。

AGC007E : 看起来就感觉很牛逼。

经典结论是，按照dfn排序之后，走下来就恰好是每条边来回各一次(呃实际上结论原来用法是这个走法距离是斯坦呐树边权和的两倍)。不过这个没啥用。

二分一波，然后考虑一个爆力dp，设\(dp(u,i,j)\)表示冲进\(u\)子树并走完所有叶子，第一个走深度为\(i\)的，最后一个走深度为\(j\)的，是否有可能。

转移的时候，因为这是完全二叉树，所以遍历儿子的顺序只有两种，都试一下就好了。更好的方法是，你发现两种顺序是对称的，我们直接钦定先走左儿子也不是不可以。

如何优化?首先\(j\)越小越好，所以我们直接设\(dp(u,i)\)表示最小的\(j\)，不可行则为\(\infty\)。

然后可以看出一个单调性，也就是如果一个状态\(i\)和\(dp\)值都比另一个大，那么它没有用，这样按照\(i\)从小到大来看，所有的\(dp\)值就都是递减的。

然后你发现每次转移都是从一个前缀转移过来了，所以就可以平衡树爆力维护启发式合并了，具体一点就是我们钦定先走状态数少的儿子，然后枚举一个状态查就行了。这样是三个\(\log\)，听起来不是很可过/ll

你发现启发式合并的时候其实没必要平衡树爆力，因为两边都有序了，我们可以直接双指针扫过去，用vector维护每个点的dp即可，于是变成了两个\(\log\)。

同时收录于 省选计划R13 T3。

AGC007F : 实际上它说的是，每个字符可以控制后面的一段，后来的会覆盖先来的。好像不是很形象，怎么说呢?

比方说现在有abcde，要变成aaacc，办法是让c向后推平得到abccc，然后让a向后推平得到aaacc。

所以怎么做?看起来就是，对\(t\)中每个字符找到它在\(s\)中前面第一次出现，那么这个字符一定会向后扩展过来，然后中间它可能被砍掉。如果存在一种方法给所有这样的操作安排一下每一步怎么走，让它们不冲突，那就可行。

然后你随机想一想，发现我们可以画一个\(n\times t\)的棋盘，其中\(t\)是它的步数。然后每个字符的扩展过程都可以表示成一条折线，目标是让不同字符的折线不相交。

然后你发现连续的一段一定可以是同一个字符扩展得到的，所以我们就可以把它们变成同一条折线，目标变成让所有折线都不相交。

然后考虑一个普及组贪心，所有的折线都应该尽可能往右走，如果没走到那么就需要下一行。这个感性理解好像很对。

考虑数据结构维护，你发现我们可以从右往左考虑每条路径，最右边的路径肯定是直接就拐过去了，而后面每条路径必须贴着上一条走，那么我们用某种数据结构维护拐点，考虑一下需要支持全局往左下平移，在开头/结尾插入删除，队列即可。

AGC008A : 只需要讨论就行了。

AGC008B : 哦原来没有操作次数限制（

考虑我们从左往右搞，然后从右往左搞，这样一定可以使得除了有一段连续的\(k\)个是最后被操作的，其它所有数都是可以随意的。于是枚举这一段即可。

AGC008C : 呃看起来很简单。不过实际上确实很简单。

按照题目给的顺序，把七种块称为1到7。

你发现3和67无论如何不会用到，因为它们下面不管怎么拼都不会是平的。

所以最优方案就是把4和5分别自己拼自己，也可能有一组和一个1拼起来(都试一试即可)，然后把1自己拼自己，把2直接摞上。

AGC008D : 我们先尝试塞\(i-1\)个\(i\)，如果这样的塞完了就继续塞那些已经判定完了的，等到要求的位置就塞上需要的。

贪心地，我们先放\(x_i\)最小的\(i\)，排序即可。

AGC008E : ¿

看起来很离谱。考虑排列是环，\(p_i\)是\(i\)指向的点，\(p_{p_i}\)就是走两步。

看起来好离谱。构造逆排列\(q\)，那么问题变成\(i=a_{q_i}\)，或者\(p_i=a_{q_i}\)。这对称了，但还是很离谱¿

还是原排列吧。

考虑对于一个\(p\)的环，我们从\(i\)到\(a_i\)连边，这显然形成内向基环树森林。

更进一步地，你发现这要么形成两个环(偶环，每个点都连到前面第二个点)，要么形成一个基环树，其中基环树的树部分一定是链，也就是说每个点最多有一个儿子(环上的点最多挂着一棵子树)，否则考虑点\(u\)，它的两个儿子就不得不放在它后面，于是后面只能交替放两棵子树的点(至少有两个)，这样从\(u\)继续往上转一圈回来的时候就接不上了。

多个\(p\)中的环之间不会相互影响，因为每个环这样连之后都会出来一个环。

所以如果我们直接给每个点从\(i\)到\(a_i\)连边，那么每个环可能和一个等大的环拼成\(p\)中的一个环，也可能自己是一个环；每个基环树自己是一个环。

环拼起来的部分看起来很简单，现在问题就是怎么处理一棵基环树。考虑把每条链插入到环上去，那么为了让链在环上那个点的前一个点能接上那个点……我好像说的不是很清楚。考虑环边\(u\leftarrow v\)，以及挂在\(u\)上长为\(l\)(不包括\(u\))的链，链头为\(w\)。为了让\(v\)能接上\(u\)，我们必然在\(p\)中连成\(u\leftarrow v\leftarrow w\)或者\(y\leftarrow w\leftarrow v\)，此后环上和链上的点必然交替。一般情况下有\(2\)种方案放上这条链，但是如果链太长，以至于让后面的(或者说前面的?)链不能正常放上去，方案数就是\(0\)了，也有可能刚好挤上去使得方案数是\(1\)，加加减减判一下就好了。每条链是独立的，可以直接乘起来。

复杂度是线性。

AGC008F : 退钱，我一直以为是多次操作/jk

问题等价于求不同的Snuke喜欢的点为中心的邻域数。Sunke喜欢的点不妨称为 好点。请注意这个中心和center没有关系。

为了让每个邻域只被统计一次，我们需要考虑为每个邻域找一个代表元。

显然这个代表元最好是它的中心之一。

考虑如果存在两个点\(u,v\)满足\(\mathrm{N}(u,d_1)=\mathrm{N}(v,d_2)\)，那么我们把\(u\)向\(v\)移动一条边得到\(w\)，\(\mathrm{N}(w,d_1-1)\)必然也和它们相等，除非\(u,v\)直接相邻了，那么我们就移动半条边。于是每一个邻域\(S\)都存在一个最小的半径，并且恰好一个半径最小的中心，这个中心可能在点上，也可能在边上。我们就在这个中心处统计这个邻域，不妨把它称为最小中心。

同时可以注意到，出现重复的情况，一定是一棵子树高度不足被塞爆了，于是可以让中心远离这棵子树走一步。所以我们知道，\(d\)越小越不容易出现塞爆的情况，所以如果\(\mathrm{N}(u,d)\)以\(u\)作为最小中心，那么\(\mathrm{N}(u,d^\prime<d)\)也以\(u\)作为最小中心。所以每个点的合法\(d\)是一个前缀，如果考虑到有的点可能不是好点，那么就是一个区间。我们只需要求出上下界即可进行统计。

考虑如果最小中心在一条边\(u\leftrightarrow v\)上，以这条边为根把树提起来，不妨设子树最大深度\(f(u)<f(v)\)，那么这条边有\(1\)的贡献当且仅当\(\mathrm{subtree}(u)\)中有好点。考虑一条边是不能被操作的，所以为了保证两边对称，\(u\)子树一定被涂成全黑了，那么考虑一下你发现这条边只在一个邻域作为最小中心。

如果最小中心在一个点\(u\)上，以这个点为根把树提起来，设\(u\)各子树的最大深度分别为\(f(v_1),f(v_2),...\)，那么这个点的贡献……

• 如果这个点是好点，那么下界是\(0\)，上界是各\(f\)的次大值，因为超过这个值之后就可以往最大的子树平移

• 如果这个点不是好点，那么上界同上，下界是各有好点子树\(f\)的最小值，因为我们需要包含一个好点作为中心，就必须选完它的子树，这和边作为最小中心的情况类似

简单换根dp即可，复杂度是线性。

AGC009A : 前缀修改考虑前缀和，相当于单点\(+1\)，最后要求\(a_i,a_{i-1}\)膜\(b_i\)相同。还是不可做¿

考虑我们直接倒着做，容易证明正确性。

AGC009B : 考虑从\(i\)连到\(a_i\)，那么问题变成要把这棵树三度化，每个点建一堆虚点串成一串挂儿子，希望深度最小。按照子树高度，先干低的再干高的即可。

AGC009C : 考虑排序之后dp，设\(dp(i,0/1)\)表示考虑前\(i\)个，这一个选入集合A/B，上一个选入另一个的方案数。

直接做是\(O(n^2)\)，考虑优化，转移就是

\(1\)是对称的，其中\(w(i,j)\)表示\(i\)到\(j\)的最小邻项差。发现满足\(w(j,i-1)\geq a\)的是一个后缀，于是我们用前缀和维护，遇到差\(\leq a\)的就重置即可。复杂度是线性。

AGC009D : 考虑这个过程是说建立一棵重构树，我们考虑最后放的那个点，称它的级是树的Uninity，它会把树分成若干连通块，这类似点分治的过程，实际上我们就是要求高度最小的点分树。

考虑一个神奇贪心，我们设\(r(u)\)表示\(u\)子树最大级最小的情况下，\(u\)的级，那么我们知道如果子树里最大的级\(k\)有两个，那么\(r(u)\)至少是\(k+1\)。如果子树里最大的级\(k\)只有一个，那么我们只能确定\(r(u)\)不能是\(k\)，此时需要考虑\(k-1\)。想了想你发现，子树里每个\(r\)值，如果它到\(u\)没有更大的值，它会有贡献。如果一个\(r\)贡献两次，那么\(r(u)\)至少是这个值。如果一个\(r\)贡献一次，那么\(r(u)\)不能是这个值。

直接自底向上模拟，由于\(r\)不超过\(\log\)，用一个二进制数状压子树内的情况即可做到线性。

AGC009E : suxxsfe认为的牛逼题/se

这个合并的结构是显然的，它形成了一个\(k\)叉树。

还是考虑什么样的数\(t\)可以被搞出来。考虑每个叶子上的数\(x\)的贡献，如果它的深度是\(d\)，那么它会贡献\(xk^{-d}\)。

对这些深度取的有什么限制吗?考虑一个神仙做法，从深到浅把这看成一个\(k\)进制小数，满\(k\)个就可以合并到上一层，那么合法当且仅当\(\sum\limits_i k^{-d_i}=1\)。

现在要想搞出\(t\)，问题就是能否找到一组\(d\)，使得\(\sum\limits_i k^{-d_i}=1\)，并且\(\sum\limits_i xk^{-d_i}=t\)。

注意到\(1-t=\sum\limits_{i\text{ is }0}k^{-d_i}\)，\(t=\sum\limits_i{i\text{ is }1}k^{-d_i}\)，这一步转化是充要的，也就是说问题变成有多少个\(t\)可以写成\(m\)个\(k^{-d}\)的和，同时\(1-t\)可以写成\(n\)个\(k^{-d}\)的和。

发现\(c_i=\sum_{j\text{ is }1}[d_i=j]\)这个东西，写成\(k\)进制小数就是\(t\)，如果不考虑进退位，它的各位和应该是\(m\)。如果考虑上的话，它的各位和应该在膜\(k-1\)意义下和\(m\)相等。\(1-t\)也是一样的。

考虑dp，设\(dp(i,j)\)表示考虑到第\(i\)位，各位和是\(j\)的方案数，那么容易知道\(1-t\)的各位和是\(i(k-1)-j+1\)。转移枚举这一位填什么，显然是前缀和的形式，可以做到\(O(n^2)\)。最后枚举所有\(j\bmod{(k-1)}=m,(i(k-1)-j+1)\bmod{(k-1)}=n\)并且\(j\leq m,i(k-1)-j+1\leq n\)的位置统计答案即可。

AGC010A : 先把所有数膜\(2\)。

考虑把所有的\(1\)合并，然后把所有的\(0\)合并，做完了。有解等价于\(c_1\bmod{2}=0\)。

AGC010B : ¿

先差分，然后问题变成给差分数组依次\(-1\)，有一位\(+(n-1)\)。

你发现差分的总和恒为\(0\)，我们要求出来是否有可能把它变成\(0\)，如果可以还需要知道使用尽可能少的操作次数这样变化之后任意一个位置的值，然后看这个值膜\(\frac{n(n+1)}{2}\)是否为\(0\)。

把所有负的不停操作，如果得到了全\(0\)那就赢麻了，否则输麻了。但是我们好像不容易判断什么时候无解?

考虑多点性质，直接设每个数\(i\)被\(+(n-1)\)的次数\(c_i\)，并设一共操作\(m\)次，设原数组是\(a\)而差分是\(s\)，则有\(s_i+c_i(n-1)-(m-c_i)=0\)，于是\(c_i=\frac{m-s_i}{n}\)。注意到\(m=\frac{2\sum a_i}{n(n+1)}\)是确定的，于是可以算出每个\(c_i\)，判断是否合法(整数，正的，没有操作成负的)即可。

没法直接看出优秀性质的时候，还是要尝试硬设然后解方程。

AGC010C : ¿

考虑一个爆力想法，我们选择一个非叶结点为根，然后进行差分，设\(a_u-a_{\mathrm{fa}(u)}=s_u\)，然后就变成每次选择两个叶子，给它们的权值\(-1\)，\(\mathrm{lca}\ +1\)，\(\mathrm{fa}(\mathrm{lca})\ +1\)。

这看起来比较离谱，因为有一个\(\mathrm{fa}(\mathrm{lca})\)。

在根上面加一个虚点作为根的父亲，于是全局和不变，所以全局和首先应该是\(0\)。

考虑爆力设每个点作为\(\mathrm{lca}\)的次数\(c_u\)，那么可以知道\(s_u+c_u+\sum\limits_{v\in\mathrm{ch}(u)}c_{v}=a_u\)。离离原上谱?

影响是自底向上的，所以考虑自底向上处理每个点，记录各子树内所有叶子剩余的点权和，把这个点搞成对的即可。所以说每个点要进行的操作是确定的¿

AGC010D : ¿

看起来没有任何想法，因为那个除\(\gcd\)实在是太离谱了。

这题神了。考虑如果有一个\(1\)，那么除\(\gcd\)就消失了，此时胜负完全看总和减去\(n\)的奇偶性，这个数记为\(s\)。如果\(s\)是奇数就赢了，否则就输了。

考虑每一轮奇偶性是不变的，所以如果不考虑除\(\gcd\)，\(s\)还是决定了胜负。如果我们拿到\(s\)是偶数，唯一可能的胜利方式就是除一个\(\gcd\)使得\(s\)的奇偶性改变。你发现这个\(\gcd\)是奇数的话啥用没有，所以只可能是除一个偶\(\gcd\)才能让局势反转。注意到这样的事情发生不超过\(\log\)次。

如果一上来\(s\)就是奇数了，因为一开始\(\gcd=1\)必有一个奇数，那么先手操作一次得到两个奇数，后手只能干掉其中一个，所以后手完全无法逆转局面。

如果一上来\(s\)是偶数，并且只有一个奇数，那么先手操作一次就会除一个\(\gcd\)，并且他必然会操作，否则就输麻了。刚才说过这样的事情发生不超过\(\log\)次，所以我们递归下去检查即可。

AGC010E : grass，我以为是只换一次/jy

考虑所有不互质的数，相对位置不会改变，而互质的数可能会。这也是交换合法的充要条件。

考虑爆力确定所有不互质对的相对位置，这可以表示成一个DAG，我们在不互质的数之间连无向边，A要给边定向成DAG，而B肯定希望求字典序最大的拓扑序。

所以我们就是要最小化字典序最大的拓扑序。

每个连通块是独立的。考虑一个连通块中，肯定是先选最小的那个，那么它的边应该都是朝外的。

然后考虑删去这个点会把它的连通块分成几部分，每一部分分别递归即可。但是这样有可能会成环?

考虑我们从这个最小的点开始dfs，每次找到最小的还没被访问的邻接点，走过去并给这条边定向，这形成一个外向树，非树边的定向是显然的。

为什么这么做是对的?考虑如果有多个起点，B肯定是选择其中最大的开始，所以我们要取最小的作为第一个，只能是选它作为唯一的起点，不然它就完蛋了。

然后选了这个起点之后，各连通块是独立的，但是它们不能有新的起点了，所以我们要从这个起点出发开始dfs。走到最小的邻接点是显然正确的。

最后用priority_queue维护一个拓扑排序即可。

AGC010F : 硬想题。

当你完全没想法，没有发现任何性质，也没有任何感觉的时候，可以通过玩小数据来找找感觉。

如果只有两个点，两个人就会来回走，那么小的那一边就没了，相等的话还是A输了。

所以，如果是一个菊花，从根出发，可以选择一个最小的叶子来回走，如果还是不能赢那就完蛋了。

然后考虑如果一个点的邻接点都\(\geq\)它，那么先手不管怎么冲，后手都会把他拉回来。

如果一个点的邻接点有一个比它小，那么先手必然会冲过去，然后后手就会逃跑，并且绝对不会回去，此时局势反转了。因此按照权值从小到大递推即可。

AGC011A : 摆 渡 车

直接贪即可。

AGC011B : 考虑这就是说有多少可以冲到最后。注意到每次吸收会翻倍，所以只需要吸收\(\log\)次就可以干翻所有别的，所以就爆力判能不能吸收到1e9以上即可。用set维护。

当然这个性质太多。排序递推似乎也是可以的。

AGC011C : ¿

为什么AGC每到C难度骤增（

考虑我们爆力做法就是开一个并查集然后枚举一对边。考虑考虑哪些边一定是没有用的。

你发现这行不通。fuck（

考虑一条边\(a\leftrightarrow c\)的贡献，它就是对于所有别的边\(b\leftrightarrow d\)，连边\((a,b)\leftrightarrow (c,d),(b,a)\leftrightarrow (d,c)\)。

离离原上谱，完全没思路。

考虑两个点\((a,b),(c,d)\)什么情况下是连通的。如果原图中存在两条等长的路径\(a\rightsquigarrow c,b\rightsquigarrow d\)就行，否则不行。

你发现一条边是偶环，而如果\(a,c\)或者\(b,d\)所在的连通块有奇环，那么即使两条路径不等长也能换成等长的。如果两个连通块(也可能是一个)都没有奇环，那就要求两条路径至少长度奇偶性相同，这样也能换成等长的。

特别的，只有一个点的连通块没法走一条边。

统计每个连通块有没有奇环，然后随便找一个dfs树算一种距离，然后直接计算答案即可。

AGC011D : 画一画你可以发现，我们把关着的记为1，开着的记为0，那么如果左边是1，球给左边取反之后就溜了；如果左边不是1，效果是把所有数取反，然后循环左移一位。

这个完全无法优化，考虑猜一个循环的结论。我们猜测不超过\(4n\)次必然循环。

考虑如何找出循环节，发现可以使用hash table，因为取反和shift的hash值变化都是简单的。

看题解，结论居然是 : 不超过\(2n\)次必然循环，循环长度不超过\(2\)。离离原上谱¿

AGC011E : 显然我们每次可以缩减一个极长递增前缀。然后考虑尽可能多选一点，也就是后面选上9999999，然后依此模拟，不过这是AGC E，所以不是很行。

你发现不降的数差分一下变成了不超过9个1，而差分的和等于和的差分，所以我们的目的就是用这些1拼出\(n\)的差分，然后把这些1拼起来成为若干上升数。

但是由于这个和不一定不降，考虑它的差分好像有点奇怪，我们不如再前缀和一波，问题变成要拿若干个111111这样的数拼成\(n\)。

然后考虑爆力设我们选了\(k\)个，它们拆成\(9k\)个111111，其中在\(i\)位结束的有\(c_i\)个，那么有

当然爆力移过去，我们得到

然后你发现两边并不独立，这整个式子只能等价于\(9n+9k\)的十进制各位和恰好是\(9k\)。

根据之前那个贪心，我们知道答案不超过\(n\)的位数。考虑直接枚举\(k\)，判断是否可行，加法爆力进位即可，因为进位有均摊，复杂度非常正确。

AGC011F : 题意比较鬼。

这个模型过于复杂，考虑如何理性表示。设\(x_i\)表示从左往右的车在车站\(i\)要等多长时间，\(y_i\)是对应的，\(sx,sy\)分别是\(x,y\)的前/后缀和，\(pre,suf\)是\(a\)的前/后缀和，那么\(sx_p+pre_p,sy_p+suf_{p+1}\)也就是在一个点\(p\)两班车出发的时间。

因为每隔\(k\)时刻还有一班车，小朋友想一想，你发现每个时间都可以\(\bmod{k}\)。那么合法的要求就是，对于每个单向铁路\(p-1\leftrightarrow p\)，有

注意空集的写法是\varnothing，\emptyset太难看了。

你发现这个式子好像说了什么，又好像什么也没说。爆力展开，区间不交等价于任何一个端点不在另一个区间里，而点不包含于一个区间的条件是或的形式，看起来和与格格不入，所以我们先不展开它。

呃这些限制看起来还是有点离谱。不过注意到\(pre,suf\)都是确定的，于是可以对那些区间进行平移，把\(sx,sy\)这些不确定的移到左边，别的移到右边。

然后就可以把下面两个取反

然后取交，也就是四个都取\(\max\)，由于\(pre,suf\)分别有单调性，最后就是

然后你发现每一步都是充要的，所以问题变成……¿好像不是很对，这里有点奇怪啊……

你发现我们把\(sx,sy\)中的一个取反(这里认为是\(sy\))，也就是变成前缀和能够得到相当好的单调性，也就是它们的和会变成单增的。注意到每趟车在起点站停靠的时间是随意的，也就是说我们可以操纵\(sx_n\)，所以它就可以是\(k\)的倍数，于是它就被膜没了。这非常好。

问题现在变成了，你有一排区间，从左往右走，每次不能走进某一个区间。取一个补，然后注意到区间的补在膜意义下还是区间，于是问题变成每次必须走进某一个区间。

直接贪心好像很复杂，考虑一个dp，设\(dp(i,...)\)表示\(i\)步之后停在每个位置的最小路程，那么我们只需要支持所有点转移到一个区间，区间推平成inf，推一个简单的式子，然后线段树维护即可。

AGC012A : 考虑一个简单想法，你希望尽可能把大的放进去作为中位数，所以我们就放一个最大的，放一个次大的，然后放一个最小的。

你发现这样必然是最优的，做完了。

AGC012B : 图邻域，看起来很牛逼。

不过实际上是普及组题。考虑我们每个点实际上只需要有10个标记，然后一个标记可以变成邻接点上规模\(-1\)的标记，从大到小依次推即可。每层标记个数都不超过\(n\)，会推出\(2m\)个，于是复杂度是\(O(d(n+m))\)。

AGC012C : 考虑一段长\(k\)的a会发生什么，你发现它的贡献是长度是偶数的子序列个数，而长度为偶数的子序列个数恰好是总数的一半(\(\sum_{i=0}^n(-1)^i\binom{n}{i}=[n=0]\)，这里不算长\(0\)的所以还要减去\(1\))，于是我们可以利用这个用\(k+1\)位拼出\(2^k-1\)。

这看起来类似于二项堆那一套。这个需要的个数是\(\log^2\)级别，所以就爆了。考虑点别的做法。

考虑啥呢?我们尝试从中间插入一些别的字符来增加控制这个值的可能。

比如我们现在在两边各放了\(a\)个a，中间放了\(b\)个b，那么子序列个数就是\(2^{2a-2}2^{b-1}-1\)。看起来还是不是很好。

考虑能否通过某种方法简单快速地操纵整体的子序列个数。发现有\(100\)种字符，我们考虑先放\(1,...,100\)在后一半，另一半考虑放一个排列，那么答案就是它的上升子序列个数。

考虑这个上升子序列怎么做，我们从小到大依次加入每个数，如果加在最后答案就会\(\times 2\)，如果加在最前面就会\(+1\)。二进制拆分即可。

AGC012D : 这是一个置换群，所以问题变成求出所有置换。然后复杂度就上天了。

考虑如果全是一个颜色怎么做。你发现我们可以从每个球出发向能和它换的球连边，然后找到所有连通块，连通块内部可以换出任意置换。这个怎么做?你发现每个连通块只扩张不缩小，所以我们可以利用这个均摊来硬做，也就是开一个链表或者并查集，链表就是把每个连通块缩成一个点，并查集就是每次跳到下一个连通块。

然后你发现一个离谱性质，每个球连向的是一个前缀，因此最小的球一定在唯一的一个大连通块里，和其它所有球连边，而不能和最小的球连边的球显然是孤立的。

考虑现在有不同颜色怎么做。首先可以对每个颜色内部跑一个刚才的东西，现在问题是我们需要删掉每一种颜色再考虑它的贡献。能否分治一波硬上?

呃好像用不着。我们当前要处理颜色\(c\)，那就把颜色\(c\)都拿出来，开一个并查集维护所有的连通块，一会再扔回去。然后正常做即可。使用set维护，复杂度是\(O(n\log n)\)。

呃好像还是用不着。考虑还是刚才的东西，我们考虑重量最小的球，那么其它颜色都可以向它连边，而它的颜色内部就向除了这个颜色的重量最小的球连边即可。

最后答案就是\(\prod_S\frac{\vert S\vert!}{\prod_C\vert S\cap C\vert!}\)，其中\(S,C\)分别枚举连通块和颜色。注意到实际上只有一个连通块，所以就简简单单了。

AGC012E : 注意到jump不超过\(\log\)次。

考虑爆力怎么做。先把起点所在的距离在\(v\)以内的连通块求出来，然后就先爆力遍历这个连通块。接下来就要出问题，我们不使用jump就出不去了，问题是jump到哪里。

求出所有距离在\(v/2\)以内的连通块，你发现我们应该jump到最容易分裂的那个，呃怎么说呢¿

时间倒流。现在问题变成你的水量是\(0\)，每次你可以jump或者walk，jump只能用\(k\)次，每次会让你的水量翻倍，walk距离不能超过当前水量。

每次jump之后会合并一些连通块，这形成一个森林，问题变成有一个\(O(n\log n)\)点的森林，每个深度可以控制一个点，如果控制了一个点的所有儿子也可以控制父亲，要控制第一层所有点，求第一层选的点可能是哪些。

注意到第一层点数只有\(\log\)级别，否则必然全无解，所以我们可以钦定每个第一层的点跑一遍。考虑状压dp，因为每个点代表一个区间，我们设\(dp(S)\)表示已经选了\(S\)中的层，覆盖了一个前缀，这个前缀最远可以覆盖到哪里。转移贪心即可，枚举每个深度，用能接上的右端点最大的区间来转移，可以每个深度开一个vector，按左端点排序做到一个\(\log\)。总共是三个\(\log\)¿

考虑怎么砍去一个\(\log\)，你发现把那个vector里面每个深度离散化一下就好了。

考虑怎么再砍去一个\(\log\)，你发现我们同时处理前缀和后缀的dp值，枚举第一层选的点和一个状态，看另一边有没有能拼起来的状态，对另一边法嘛塔一下就好了。

AGC012F : 传 世 经 典

考虑如何判定。要想让一个数作为中位数，我们就在它需要成为中位数的时候把它加进去，如果它已经加进去了怎么办?如果它现在不是中位数，那就尝试加两个剩下的中最大的或者最小的把它调整过去，否则就加一个最大的一个最小的让它别动。

注意到加最大/最小的一定正确，因为它们已经不可能成为中位数了。所以它是正确的。

现在它还不够好，我们要描述什么情况下可以调整过去。假设现在已经加入了\(S\)，希望把其中的\(x\)变成中位数，那么如果\(x\)到现在的中位数还隔了一个数，或者剩下用来调整的值不够用了，那么就不可能调过去，否则一定可以。

实际上 不够用了 有更好的描述。我们从小往大放一遍，从大往小放一遍，就可以求出每个中位数的上下界，如果不超过这个上下界，那么调整用的最大/最小值一定不会被用完。

开始考虑dp。设\(dp(i,j,k)\)表示当前决策到第\(i\)个中位数，这个数左右各有一个之前的中位数(没有则是边界)，两边分别还有\(j,k\)个可以选的数的方案数。转移枚举上一个选了什么，决策保留当前数，还是选两边的一个数即可，复杂度\(O(n^4)\)。

AGC013A : 线 段 树 优 化 d p

贪。

AGC013B : ¿

挑 战 哈 密 顿

模拟即可。

AGC013C : 独 木 桥

可以用独木桥的trick，我们先求出来最后所有蚂蚁的位置，但是我们此时不知道哪个是哪个。发现蚂蚁们的相对顺序是不变的，所以只要知道\(1\)是哪一个就好了。

那么怎么才能知道\(1\)是哪一个呢?想了一下，你发现\(1\)的位置确实不好算。

考虑我们算这个环\(0\)右边第一个位置是哪一个。你发现每有一只蚂蚁从左往右冲过\(0\)，\(0\)右边的这个蚂蚁编号就会\(-1\)，反之就是\(+1\)，当然这里都是膜\(n\)的。模拟即可。

AGC013D : 考虑怎么做。

如何判定?呃这就好像有两个\(\pm 1\)序列，一开始两边各有若干\(1\)，我们每次先往其中一个加入一个\(-1\)，再分别加入两个\(1\)，再加入一个\(-1\)，如果出现前缀和\(<0\)了那就完蛋了，否则啥事没有。

设\(dp(i,j)\)表示考虑前\(i\)次操作，一边当前和是\(j\)的方案数，那么另一边就是\(n-j\)。转移就枚举这两个放什么即可。呃但是有个问题，我们不好赋初值，因为多种一开始的情况可能会导致相同的结局。

这个好说，二项式反演一波就结束了。

吗?好像不行。考虑如何去重，你发现这个看起来就像折线，我们可以强制把其中一条平移到与\(0\)恰好有交点，我们就在这里统计这种情况，加入一维\(0/1\)即可。

AGC013E : classic。

考虑一个爆力dp，设\(dp(i)\)表示到\(i\)的答案，那么转移就是

看起来很像是前缀和优化之后矩阵快速幂，不过这里带一个平方，看起来很离谱。不过我们尝试硬做!

考虑\((i+1-j)^2=(i-j)^2+2(i-j)+1\)，这样正好可以从\(dp(i+1)\)里面拆出一个\(dp(i)\)。考虑转移

遇到了僵局。考虑这么一个事情，我们不能把\(i\)和\(dp\)放在一起，因为这样它就不线性了。这里的关键性质是\(i-j\)是从\(0\)开始的，每次增加\(1\)，非常适合递推，所以我们不要把它拆开。

看起来已经做完了。然后就段内快速幂，段之间特殊处理即可。

存在一个组合意义的做法，但是这个题真的需要组合意义吗?

AGC013F : 我怎么连单次询问都不会（

给你一个序列，肯定是贪心匹配。但是现在我们需要选择这个序列，那就完蛋了。

考虑这个过程类似一个括号匹配，如果一开始我们全选正面，现在我们能做的操作就是，可以把一个左括号往前移动，代价是\(1\)(反面比正面大的就不能这么做了)。考虑前缀和，这个左括号往前移动之后，会导致一个区间的前缀和都\(+1\)。

所以我们考虑，问题变成有一个序列和若干区间，你可以选择一些给它们\(+1\)，要求最后序列全是正的，最小化选的个数。

考虑一个贪心，我们从左往右依次考虑每个负数，讲道理因为前面没有负数了，我们应该选择覆盖这个数的区间中右端点最右的。用堆维护，复杂度是\(O(n\log n)\)。

怎么处理多组询问?考虑首先我们枚举\(n+1\)选哪个，这样每个询问变成了两个询问，然后它们每一个都会做一次后缀\(+1\)。

扫描线。考虑把这个按照\(+1\)的后缀分成两段，前面可以顺着贪下来，但是后面就不太行了。

有一个非常强行但是很精妙的做法。考虑我们先从右往左贪一遍，让每个数都至少是\(-1\)，这一步对每个询问都是正确的。然后再从左往右贪，这样扫到一个询问的时候，它的后缀至少是\(-1\)，得到它的\(+1\)之后就至少是\(0\)了。总复杂度\(O(n\log n)\)。

AGC014A : 这是某种取平均，所以我们猜测若干轮之后差趋近于\(0\)，此时一定停止或者循环，所以模拟1e5轮，如果出现过奇数那就出现了奇数，否则就判定为循环。

AGC014B : 看起来有点厉害。考虑这个操作等价于链\(\mathrm{xor}\)，于是我们考虑这相当于给两个点的点权都\(\mathrm{xor}\)上\(1\)，边权是点权的\(\mathrm{xor}\)，于是问题就是能不能找到一棵生成树满足每条边的端点点权相同。如果所有点权都相同那一定可以，否则一定不行。

AGC014C : 6e5的格子，看起来\(n^3\)并冲不过去。

考虑如果我们选了一条路径，怎么求它的最小代价。容易发现最优策略就是一直走到不能走，然后解锁路径上接下来的格子，那么你发现因为可以解锁\(k\)个，我们后面一定可以走满，所以如果第一段长度不到\(k\)，答案是后面的段数\(+1\)，否则是总的段数。

这两个能不能统一一点?好像不能。

不过其实也不用。我们枚举第一段的结尾在哪，然后求出到起点和边界的最短路，这里到边界是可以走锁的，而到起点不行。直接更新答案即可。

AGC014D : 也就是说，后手要让任意一个白点都有一个黑的邻接点。

先考虑一些简单情况。你发现如果只有一个点，A就赢了（

如果有两个点，A必然输掉。

如果有三个点，A必胜。

你发现三个点很有意思，因为它染了一个点，这个点有两个邻接点是叶子。我们直接猜测，如果存在一个点，它的两个邻接点是叶子，那么A染这个点就赢了，否则A就输了。

A赢是简单的，但是为什么否则A会输呢?好像也不一定。

换一个结论。我们每次找一个叶子，如果它的父亲还邻接一个叶子，那么A就赢了，否则删掉这个叶子和它的父亲，也就是A选择父亲，让B选择这个叶子，那么结果不变。

考虑这么删到最后，如果啥都不剩了，A就输了，否则A就赢了。但是删叶子的顺序是否有影响呢?好像没有。

实际上这就是求树的完美匹配。如果存在完美匹配，那么B按照匹配走即可，否则A必然获胜。

AGC014E : 1e5 6s，不会是真的吧?

猜一手网络流，毕竟这题分块还是太离谱。不过也可能是巨大多\(\log\) ds?

考虑这相当于给边找一个对应关系，然后安排一个顺序。如果我们让\((u,v)\)被删掉，并操作得到\((u^\prime,v^\prime)\)，那么就必须满足链\(u^\prime,v^\prime\)上有边\((u,v)\)，并且\((u,v)\)是链上第一个被删的。

注意到我们每次删掉的都是只被一条链覆盖的边，所以我们树剖一发，每次查询全局最小值即可。做完了。

考虑点刺激的，我们发现最后加入的红边一定和它删去的蓝边重合，所以我们可以先确定最后这些边。然后就会形成一些链，每条链上可能会再选一些，然后你发现能这么选等价于两边是被红边连通的，于是我们正着用并查集维护即可。

AGC014F : 楼 房 重 建

考虑这个过程看起来是什么样子。

我们找到所有的前缀最大值，然后移到最后面去。这个过程之后，新的前缀最大值，就是原来没动的元素的前缀最大值，加上动了的元素的一个后缀。那个后缀就永远不会变化了，所以我们至少知道每次至少会固定一个元素，进行\(n\)轮必然结束。

注意到每个数被移动到最后之后，可能会把前面更大的挤掉，所以这个事情好像不是很容易考虑。类楼房重建线段树模拟听起来也不是很可行。

考虑换个扫描线方向。我们考虑\(1\)的位置，把它删去得到一个新的序列，如果这个序列可以用\(t\)步排好序，那么我们考虑\(t\)步之后\(1\)的位置，如果它在第一个那么原序列也可以用\(t\)步排好，否则必然需要\(t+1\)步。

现在问题是怎么判断\(t\)步之后\(1\)的位置。没什么想法。

这是递推，所以我们已经知道了\(2\)的位置。考虑原序列中\(1\)和\(2\)的位置 :

• 如果\(1\)在\(2\)前面，那么一次操作中，如果\(1\)在第一位，那么\(1\)会冲到最后去，否则顺序不变，特殊情况是如果\(2\)紧跟在\(1\)后面则顺序不变。

• 如果\(1\)在\(2\)后面，那么一次操作中，如果\(2\)在第一位，那么\(2\)会冲到最后去，否则顺序不变。

然而即使我们知道\(1,2\)的位置规律，还是没有什么用，我们并不能依此做任何事。怎么才能跟开头挂上钩呢?

有一个爆力想法。考虑新序列排好序的前一步(如果新序列直接有序，是平凡的)，\(2\)必然不会放在第一位，否则\(2\)将会被移到后面去，则下一步仍然排不好序。设此时的开头为\(x\)，爆力考虑三个数的顺序。

• 如果是\(1,2,x\)，那么操作一次变成什么依赖于\(x\)是不是前缀最大值。结论是\(x\)要么不是前缀最大值，要么处在开头。证明也不困难，如果\(x\)是前缀最大值，那么它此后再也不会回到前面来了，而我们要求\(x\)在最后一次操作前处于第一位。所以它一定变成\(x,1,2\)或者\(2,x,1\)，或者不变。

• 如果是\(1,x,2\)，那么会变成\(x,2,1\)，或者不变。

• 如果是\(2,1,x\)，那么会变成\(1,x,2\)，或者不变。

• 如果是\(2,x,1\)，那么会变成\(x,1,2\)，或者不变。

• 如果是\(x,1,2\)，那么会变成\(1,2,x\)，或者不变。

• 如果是\(x,2,1\)，那么会变成\(2,1,x\)，或者不变。

你发现它总是循环移一位或者两位，或者不变。

注意到最后一次操作之前顺序一定是\(x,1,2\)或者\(x,2,1\)，其中\(x\)在第一位，而操作之后分别变成\(1,2,x\)和\(2,1,x\)，后者需要再一次操作。

那么猜测如果一开始的顺序和\(x,1,2\)循环同构，就不需要多一次操作，否则需要。依此递推答案和\(x\)即可。

AGC015B : 考虑我们要从\(i\)冲上去，那么当然是先向下冲到最近的上行，然后向上冲，向下是对称的。做完了。

AGC015C : 树满足\(n-m=1\)，森林满足\(n-m=k\)，\(k\)是树的个数。直接前缀和支持数点即可。

AGC015D : 每一位好像不是独立的。吐了/hanx

爆力讨论题。

考虑\(l,r\)最高的不同位，那么一定是\(l\)在这一位上是\(0\)而\(r\)是\(1\)，而更高的位都可以忽略。我们找到\([l,r]\)中第一个这一位是\(1\)的数\(k\)，那么你发现

• \([l,k-1]\)内部任意\(\mathrm{or}\)的结果还是\([l,k-1]\)

• \([k,r]\)内部任意\(\mathrm{or}\)的结果是\([k,\mathop\operatorname{or}\limits_{i=k}^r i]\)

• 两部分之间\(\mathrm{or}\)，看起来比较复杂。注意到最大值是\(2k-1\)也就是全\(1\)，最小值是\(k+l\)，然后这之间所有数都可以通过在左边选一个，右边选\(k\)得到，所以这个结果就是\([k+l,2k-1]\)。

现在问题是怎么求那个连\(\mathrm{or}\)。考虑\(r\)中次高的\(1\)位，此下的位都可以是\(1\)，而此上都不行，于是就做完了。

求个并即可，不想求并可以容斥一下减去交。

AGC015E : 爆力就是\(a,b\)相撞于\(\frac{x_a-x_b}{v_a-v_b}\)，所以可以处理出来一个相撞的顺序，然后问题就变成每个点都有一条时间递减的路径到一个被染色的点。爆力搜出让每个点可行的集合，然后看起来就很能做了?

呃直接算好像还是不是很行，我们进行容斥，钦定若干集合让它们里面的数都不被选，剩下的随便选。这好像还是很离谱/hanx

太奇怪了。看起来这个题一定有什么特殊性质。

那个式子看起来很可爱，把所有点\((v_i,x_i)\)画到平面上，那么两个点的相撞时间就是连线斜率，如果斜率是负的那就不会相撞。想象有一个指南针从斜率\(0\)转到\(\infty\)，转到哪里，那个斜率的线就会发动。

所以我们知道一个点可以传播到左下或者右上的所有点，那么右下和左上呢?考虑一个点\(a\)传到右上方的\(b\)之后，这个\(b\)会继续传自己的左下方，最终把横坐标在\(a\)到\(b\)的点都传上。

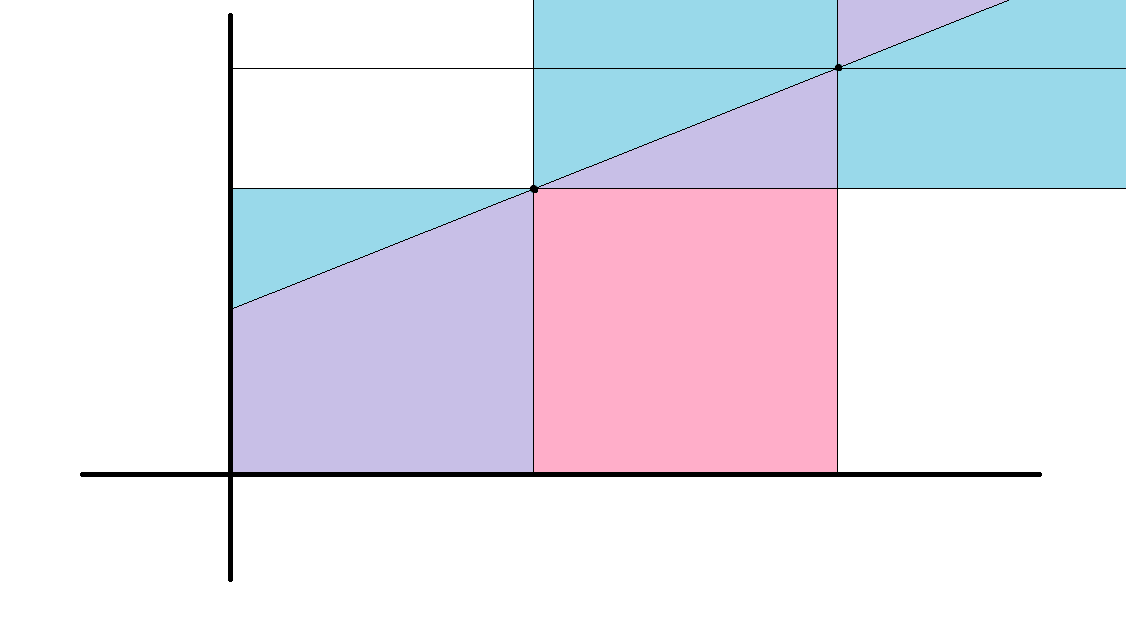
蓝色的是一开始我们选的点感染的部分，粉色是它感染到的一个点感染的部分，而紫色是同时被两个点感染的部分。

所以按照横坐标排序，每个点的影响是一个区间，也就是它右上方最右的点，到它左下方最左的点。

问题变成有若干区间，选一些覆盖全局，前缀和优化dp即可。

AGC015F : 看起来很牛逼。

众所周知Fib数是取到最值的最小方案，所以最大值已经做完了。

有多少对呢?不知道（

考虑一件非常奇怪的事情，我们考虑所有\(a\leq b<2a\)的对，别的都可以表示成\((a,b+ka)\)，对于相同的\(a,b\)，\((a,b+ka)\)们做辗转相除的次数应该一样。

打表可以发现达到最值的这样的对非常少，最值为\(k\)的时候，达到它的只有\(k\)个。

于是我们可以暴力预处理这些对，方法是第\(k+1\)层的对就是第\(k\)层反着做一次辗转相减，再加上一项……哪一项呢?仔细观察，发现是\((f_{i+2},f_i+f_{i+2})\)。做完了。

AGC016A : 枚举最后变成了哪个字符，然后模拟即可。

AGC016B : 看起来很有趣。

考虑两只猫猫看到的颜色种数相差不会超过\(1\)。如果超了那就没办法了。

然后考虑现在整个序列只有两个数，\(x,x+1\)。那么我们构造一个，所有拿着\(x\)的猫猫拥有一种独一无二的颜色，所有\(x+1\)的猫猫拥有同一种颜色，这个构造看起来很可行。

注意到如果\(x+1\)只有一个那就不行了，因为这样它也拿着独一无二的颜色了。所以Yes当且仅当序列中只有\(x,x+1\)，并且\(x+1\)出现至少两次，并且依据上面构造算出来的颜色数和这个序列匹配。

呃如果\(x+1\)没有了呢?此时构造就是所有猫猫颜色都相同或者都不同，也就是序列全是\(1\)或者全是\(n-1\)。

AGC016C : 如果恰好可以用\(h\times w\)的矩形密铺\(H\times W\)的矩阵，那必然无解。否则考虑每个数被算入多少次，你发现算入总和的系数是一样的，但是算入所有子矩形的和的贡献则是边上小中间大。所以我们在中间放满大负数，边上放上大正数，这样看起来就很可行。

想了想你发现，边上的贡献还是很大，我们可以在四个角摆上1e9，现在问题是怎么调回来。

调不回来!对四个角求和，就完蛋了。但是这个策略已经很强了啊!

考虑点别的构造，我们在所有膜\(h,w\)都是\(0\)的点放上\(-hw\)，别的点放\(+1\)，那么最后所有子矩形显然是满足条件的，总和呢?

你发现每个大负数和它作为左下角的子矩形抵消了，得到\(-1\)，而会有一些边角料不能抵消，如果这些边角料足够大就行了。

注意到一个很好玩的事情，只要有一个边角料，我们就可以通过把\(1\)放大到\(x\)，而把大负数搞成\(-x(hw-1)-1\)从而做完了。

AGC016D : 呃你发现这个操作之后全局xor和会变成被操作的数，所以相当于有一个寄存器，一开始这里面是全局xor和，然后每次可以交换寄存器和一个数。注意到这是交换，所以寄存器里总是剩下的数的xor和，所以我们可以求出一开始和最后的寄存器，如果它们不重排同构那就无解。

然后就简单了，我们求出一开始到最后是怎么换的……呃可能有重复的数……

考虑既然有重复了，我们就不能再用和位置相关的东西了。考虑一个位置\(i\)上的两个数\(a_i,b_i\)，如果\(a_i\neq b_i\)，我们就需要把一个\(b_i\)换过来，然后考虑交换形成了一条链，那么我们爆力从\(b_i\)连到\(a_i\)，表示有一次寄存器是\(b_i\)，然后换给了\(a_i\)。

你发现每个连通块看起来好像形成了一个环，又好像没有，仔细想一想你发现它大概是若干环的并(¿)，于是我们可以猜测必然可以不浪费一次操作，除了在连通块之间转移的时候需要一次操作。寄存器中的数需要特殊处理。

AGC016E : 考虑爆力怎么做，我们先枚举一对，然后贪心扫过去，如果操作不涉及任何一个我们钦定的那就随便选……这对吗?

这不对。有可能我们干掉了一个以后能给我们挡枪的。¿那还怎么玩啊

考虑一个奇怪做法，我们设\(f(i,j)\)表示一对是否可能都生还，那么每次操作之后的改变是什么样的呢?如果操作了可能都生还的对，那么只有这一对变成不可能都生还了。否则，所有含有\(i,j\)的都不可能都生还了。

直接爆力，复杂度\(O(nm)\)。问题是正确性?

感觉上就完全不正确，因为它们完全不独立。

考虑点阳间做法，我们倒着做(而不是时间倒流)，如果我们希望保护\(i\)，而有一次遇到了\((a,i)\)，那么前面也必须保护\(a\)了。维护一个需要保护的集合，如果哪次遇到这个集合中的两个被操作了，那就完蛋了，否则就赢麻了。

这个复杂度是\(O(n^2m)\)，考虑优化。我们先枚举一个，算出这个集合，然后再枚举一对。

如果两个集合没有交，那就做完了，这一对必然可以。如果有交呢?你发现交中的需要同时保护两边，那就完蛋了，所以一定不行。

使用bitset求交，复杂度\(O(nm+n^3/w)\)。

AGC016F : 看起来很牛逼。这是两个有向图游戏，你发现这就是说\(1,2\)两个点的SG值不相等的方案数。

考虑一个dp¿呃等等DAG有啥阶段……

找不出阶段，我们考虑是不是扫描线方向出了问题。发现我们可以每次找到SG值最小的点来转移，也就是说考虑一张子图\(S\)必然有SG值最小的点，我们把这些点钦定出来作为\(T\)，那么\(S-T\)中的所有点必须连向\(T\)中的至少一个点，\(T\)内部没有边，\(S-T\)内部不知道。

现在我们可以考虑一个\(dp\)了。设\(dp(S)\)表示集合\(S\)中的SG值比\(S\)外面的SG值大，并且\(1,2\)的SG值相等的方案数，那么\(S\)包含\(1,2\)中恰好一个的时候显然有\(dp(S)=0\)。

转移枚举\(S\)中SG值最小的点\(T\)，注意\(T\)要么同时包含\(1,2\)要么同时不包含。然后我们钦定\(T\)内部的边都不能连，\(S-T\)到\(T\)的边先给\(S-T\)中每个点钦定一条然后剩下随意，设\(c(S,T)\)表示 \(S\)到\(T\)的边数，那么连边的方案数是\(\prod\limits_{i\in S-T}(2^{c(i,T)}-1)\)。

统计答案的话，答案就是\(dp(\varnothing)\)。

枚举补集的子集，可以直接枚举补集的子集，也可以枚举超集再减去自己。枚举超集看起来是这样的 :

1
for(int T=S;T<(1<<n);T=(T+1)|S)

AGC017A : 全都膜\(2\)，然后就是选择一些包使得它们的xor和为\(0\)或\(1\)。背包即可。

AGC017B :

考虑差分，问题变成找\(n-1\)个绝对值在\([c,d]\)的数使得它们的和是\(b-a\)。考虑一个dp，你发现一个数会贡献到两个区间，然后这两个区间会贡献到三个区间，这三个区间会贡献到更多的区间，依此类推。麻了?

dp太扯了。考虑点阳间做法。

直接考虑这些区间是什么样子。现在我们拿着\(0\)，然后会变成\([-d,-c],[c,d]\)，然后变成\([-2d,-2c],[c-d,d-c],[2c,2d]\)，然后变成\([-3d,-3c],[c-2d,d-2c],[2c-d,2d-c],[3c,3d]\)，然后变成\([-4d,-4c],[c-3d,d-3c],[2c-2d,2d-2c],[3c-d,3d-c],[4c,4d]\)……呃好像已经发现了什么。操作\(k\)次之后，所有的区间就是\([ic-(k-i)d,id-(k-i)c]\)，其中\(0\leq i\leq k\)。枚举哪个区间即可。

实际上还有更阳间的做法，发现所有这些区间长度都相等，所以我们求出最大的满足\(ic-(k-i)d\leq b-a\)的\(i\)，这个区间一定不劣。直接整数除法就得到\(O(1)\)。

实际上还有更更阳间的做法，我们枚举有多少个正数，给正的全部\(-c\)，负的全部\(+c\)，然后就可以贪心构造了。

AGC017C : 注意到这是AGC，所以我们猜测这题没有数据结构/jy

考虑单次怎么做。

考虑先给所有数从小到大排序，然后排成一排，想象一堆柱子，高度就是数值。那么考虑每个连续段，你发现其中最右边那个必须满足\(i=a_i\)，这很是合法的充要条件。

于是现在每个连续段都有一个应该在的位置，我们扫过序列，如果现在已经有了\(c\)个\(a\)，现在又来了一个\(a\)，那么它应该排在\(a-c+1\)的位置上。有多少个位置不对的数，就需要多少次操作。已经做完了。

AGC017D : 看到2e5就安心了/cy

看了看你发现这就是Green Hackenbush，结论是一个点的SG值是子树的SG值的xor和再+1，而这里根不能删所以就不+1了。好像也有说是+1的xor和的?忘了，反正差不多（

AGC017E : 过于经典。建一排值域桶，给相对应的接口连边，跑欧拉回路分解。

AGC017F : 奇怪题。

从上往下做显然是不行的。考虑从左往右做，你发现每条线只需要知道上一条线的形态，这就很好。直接做复杂度是\(O(4^nm)\)。

如何优化?考虑我们换成轮廓线dp，复杂度就是\(O(2^nn^2m)\)。具体一点就是设\(dp(i,j,k,S)\)表示考虑第\(i\)条线的第\(j\)步，上一条线在这一步的横坐标是\(k\)，两条线合起来的状态是\(S\)。

然而还是冲不过。发现我们存\(k,S\)两维，还是为了记录上一条线对这条线的限制，那么我们不如直接换成一维\(S\)表示当前这条线最左可以怎么走，也就是一直往左走直到撞上上一条线，然后沿着上一条线走，得到的形态。这样复杂度就是\(O(2^nnm)\)了，实现起来比较好玩。

之前说csp2021不可能出轮廓线dp，没想到T4真有一档部分分给轮廓线?不过能写轮廓线的人早看出来网络流了吧（

AGC018A : ¿

这居然是橙色的，我需要想一年（

考虑我们可以凑出任意系数(只要结果是正的)，所以就做完了。好扯啊（

AGC018B : 最大值最小，二分答案?

二分之后考虑如何判定，考虑每个人先选第一志愿，如果有爆了的就取消掉，然后再找到这些人让他们改选第二志愿，如此迭代直到没有爆了的。

注意到二分可以省去，因为我们可以直接不停找到最大的把它取消掉，同时更新答案。

AGC018C : 呃这个问题看起来非常简单。

费用流。建图是从\(s\)连到三个点\(x,y,z\)，然后三个点连到所有点，所有点连到\(t\)。容量和费用懂的都懂。

根据经典结论，增广路不会经过同一个点多次。手动枚举所有可能的增广路，有

• 选一个金/银/铜

• 选一个(银/铜)/(金/铜)/(金/银)，把它换成金/银/铜，同时再选一个(银/铜)/(金/铜)/(金/银)

• 选一个……总之就是换两次。你发现这个可以拆成换一次，然后消一个负环。

总之最后我们就开九个堆，维护没选的最大值，和换一次的最大值即可。

然后你发现我们都搞出消负环了，不如一上来就直接选完，然后直接消负环，这样就不需要那三个堆了。

考虑所有的负环 :

• 把一个金换成银，一个银换成铜，一个铜换成金

• 把一个金换成铜，一个铜换成银，一个银换成金

• 把一个金/银/铜换成银/铜/金，一个银/铜/金换成金/银/铜

做完了。

据说可以wqs二分，但是我不理解它的正确性(费用流可以证明高维的凸性吗?)，所以还是不讲了。

AGC018D : 挑 战 哈 密 顿

Banana banana me, how to solve D/kel

这个问题好像很经典，我们找到重心，这样就可以使得每次移动都跨过重心，而别的点因为最大子树大小超过一半，所以一定不行。递归到各个子树，类似于点分治。

AGC018E : 大量公式，极好的组合数学练习题。

首先考虑在中间统计答案，也就是枚举中间休息的那个点，算走到两边矩形的方案数，然后乘起来求和。然后你发现这个好像很难做（

先来点简单的。我们考虑从一个点\((0,0)\)出发往右往上走到一个矩形中任意一点的方案数，首先我们枚举这个点，然后用组合数算方案数。

呃这个咋做啊（

考虑首先进行差分，问题是求

我们直接上指标求和，反转之后再求和一次

草，为什么这个东西这么简单/jk，那么一个点到一个矩形\([l_1,r_1]\times[l_2,r_2]\)就是\(\binom{r_1+r_2+1}{r_1+1}-\binom{r_1+l_2}{r_1+1}-\binom{l_1+r_2}{l_1}+\binom{l_1+l_2}{l_1-1}\)了。

现在我们会算这个了!枚举中间那个点还是没有前途，考虑一个牛逼做法，我们枚举进入中间矩形那个点，枚举离开的那个点，计算方案数然后乘上中间的长度(选休息的点的方案数)，显然确定了这两个点之后中间的长度是确定的。

写出式子，你发现中间的长度实际上是这两个点的两维坐标和的差，于是我们可以拆开两个点的贡献，做完了。当然第一感觉可能不是这个，但是还是要尝试各种做法，然后注意一下能不能拆贡献之类的来降低复杂度。

AGC018F : 看起来好离谱。

每个点只有两种情况，也就是和为\(1\)或者\(-1\)，只需要确定这个就可以唯一确定每个点的点权，如果第一棵树确定的点权同时满足第二棵树那就赢麻了，否则输麻了。

然后考虑如果一个点的点权很离谱，那么要么就是另一棵树上它的点权同样应该很离谱，要么就是，呃好像没有别的要么了。

我们进行一个结论的猜，每个点的点权都可以是\(0,1,-1\)的一个。根据儿子个数的奇偶性可以判断一个点的点权是\(0\)还是\(\pm 1\)，如果两棵树之间这样产生了矛盾则直接无解，下面的问题是\(\pm 1\)的点怎么确定点权。

等等，这个\(0,\pm 1\)就让人想起来一个题叫Mike and Fish，说的是加边消去奇点然后对欧拉回路上每条边交替定向之后，原图上每个点出入度之差是\(0,\pm 1\)。

我们考虑一条有向边的含义，认为它是给指向的点点权\(+1\)，而另一边点权\(-1\)。这样它只会影响两个子树的点权和。

然后呢?我们把两棵树都搞出来，按照树上连边，然后每个点如果度数是奇数，就把两棵树上的这个点连起来，然后跑欧拉回路并交替定向。如果一个原来是奇度的点，在两棵树之间的连边是从第一棵树指向第二棵树，那么它的点权是\(1\)，否则是\(-1\)。树上的部分完全可以保证点权合法，这看起来还是挺正确的。

同时欧拉回路交替定向和二分图染色有着奇怪的联系，我不知道是什么联系，但是反正这个题也有二分图染色做法。

AGC019A : 首先如果大的可以被小的凑出来，那么大的就没救了。然后猜一个结论，我们每次尽可能装最大的，剩下很少的时候爆力背包，它必须得过。

然后你发现一些很有趣的事情。这个量是整数，所以我们把\(0.25,0.5\)都变成\(1\)，然后判全\(1\)和尽可能多\(2\)哪个优即可。

AGC019B : 看起来很有趣，然而其实没有（

考虑如果翻\([l_1,r_1],[l_2,r_2]\)得到的串相同，那么

• 如果它们不相交，它们必然都是回文子串，得到的都是原串

• 如果它们相交但不包含，那么讨论一下，它们也必然都是回文子串

• 如果它们包含，那么讨论一下，它们不一定都是回文子串/jy，比如aabca中翻\([1,5]\)和\([2,4]\)是一样的

本来打算猜测翻完了相同当且仅当翻两个回文子串，但是第三个情况看起来比较离谱。

注意到这个包含看起来很有趣，你发现如果一个区间两边相同，它和它砍掉两边得到的区间翻完了必然相同。考虑每个两边不相同的区间，它们翻出来的是否都不同?

• 如果不相交，显然不同

• 如果相交但不包含，还是不同

• 如果包含，还是不同

于是就证完了。最后答案就是所有区间减去每种字符作为端点构成的区间的和。这句话可能比较混乱，但是如果你看了上面你就懂了（

AGC019C : 首先假设终点在起点的右上，那么我们走每一条大路都必然是往右上走。注意到在喷泉处拐角是优的，而穿过喷泉是劣的。

你发现这看起来像是lis类似物，于是我们就对于喷泉\((x,y)\)，把它看成\((x-1,y)\rightarrow(x,y+1),(x,y-1)\rightarrow(x+1,y),(x-1,y)\rightarrow(x+1,y),(x,y-1)\rightarrow(x,y+1)\)的四个通道(当然有权值)，然后强行BiT优化dp即可。

有没有更简单的做法?考虑直接求一个lis，然后构造方案。你发现因为每行每列只有一个喷泉，我们几乎总能构造一个方案，除非这个lis从一边开始冲到另一边，此时我们不能继续拐了，于是只能冲过去。发生这种情况的时候，我们总要冲至少一个喷泉，所以只需要特判一下给它加上\(\frac{1}{4}\)圆即可。

AGC019D : 看起来好困难。一看数据范围发现才2e3?

你发现转不会发生很多，并且我们一定是把每个位置在某个位置操作了，然后转到它对应的位置去。

考虑枚举转了多少，那么我们就知道每个位置经过了什么，以及最后变成了什么。如果它没有发生变化，那么中间是啥都没问题，否则中间需要至少有一个\(1\)，我们往前或者往后找到第一个\(1\)，它必然匹配这两个中的一个。现在代价是往前转的最大值和往后转的最大值加起来。

于是我们排个序，枚举往前转的最大值，于是更大的只能往后转，小的就别往后转了，这是一个后缀\(\max\)。使用计排，总复杂度\(O(n^2)\)。

这题看起来很像icpc2020上海站的H?

AGC019E : 注意到每个位置有四种状态00,01,10,11，并且状态相同的位置除了编号是没有什么区别的。

考虑这个过程是在说什么，或者说我们怎么把这个过程转化成一个人类可以理解的过程。注意到把\(a\)和\(b\)都随机排列，等于说把\(a\)随机排列然后直接配对，然后把配出来的对随机一个顺序执行。

如果一个位置是10或者01，它的度数是\(1\)。如果是11，度数是\(2\)。

那么这是个啥?这一定是若干链和环的并。考虑每条链，它开始于一个10，结束于一个01，中间全是11。每个环全是11。链有唯一的执行顺序(10的1需要走到01去)，而环是随意的(不管怎么样都不会变化)，它们之间是独立的。

好像可以考虑dp了，但是还有一个问题是会不会算重。呃看起来不会。

于是设\(dp(i,j,k)\)表示还剩下\(i\)个01，\(i\)个10和\(j\)个11没有搞起来，一共选了\(k\)组链或者环的答案，转移枚举这一次选什么，最后除掉\(k!\)。这是\(O(n^4)\)。

前缀和，\(O(n^3)\)。还是不行!得把某一维干掉。

考虑干掉\(k\)，你发现可以。我们钦定先选链，那么假设最后只剩下\(c\)个11，此时不管怎么配对，按什么顺序执行都可以，于是方案数是\(c!^2\)。总复杂度\(O(n^2)\)。

这个做法非常强行，出到1e5的话存在法法塔做法，就是把拼接换成EGF卷积，不再赘述。

AGC019F : 看了一眼题面，以为是一眼题，再看一眼，发现不对!

呃注意一下样例解释，你的策略可以是随机的。

如果现在剩下\(c_1,c_2\)个Yes,No，那么最优策略是猜更多的(而不是以\(c_1:c_2\)的概率去猜)，如果相同则随意。这个概率是会变的!

\(n^2\)是简单的，我们考虑一个dp，设\(dp(i,j)\)表示还剩\(i,j\)个Yes,No的答案，如果\(i\geq j\)，转移就是\(dp(i,j)=\frac{i}{i+j}(1+dp(i-1,j))+\frac{j}{i+j}dp(i,j-1)\)。

这东西怎么看都阳间不起来。

感觉像是法法塔，但是法法塔肯定处理不了大小比较，所以考虑我们怎么把这个\(i\geq j\)干掉。钦点\(n\geq m\)，否则互换。显然一个状态转移会转移到一个\(i<j\)的状态，当且仅当它的\(i=j\)，这样的状态只有\(n\)个。

那么也就是说现在大部分的转移都是\(dp(i,j)=\frac{i}{i+j}(1+dp(i-1,j))+\frac{j}{i+j}dp(i,j-1)\)了!fuck，这个看起来不可能优化。

考虑点牛逼想法，可能的情况和折线是双射，每次你会猜折线往\(x-y=0\)上走，答案就是你猜中的步数除以所有情况走的总步数。总步数是\(\binom{n+m}{n}(n+m)\)。

你发现横纵分别走\(i>j\)步到\((n,m)\)的话，你猜中的方案数是\(\binom{i+j}{i}-\binom{i+j-1}{i}\)。同时，上面一格的方案数是\(\binom{i+j-1}{i}-\binom{i+j-2}{i}\)。于是\(\binom{i+j-1}{i}\)就被消去了，最后只有\(x-y=0\)上的点有贡献，我们直接计算即可。

这绝对是好题（

AGC020A : 你发现不管怎么动，距离的奇偶性不变。如果是奇数，那么最后一定可以到\(1\)，到了\(1\)之后先手就只能被逼死在角落了。否则就反过来了。

AGC020B : 考虑直接做，我们假设这一轮剩下了\(n\)个人，这一轮是\(k\)个人一组，那么上一轮剩下\(m\)个人，就有\(n=k\lfloor\frac{m}{k}\rfloor\)，也即\(\frac{n}{k}=\lfloor\frac{m}{k}\rfloor\)。于是\(n\)必须是\(k\)的倍数，并且\(m\)合法当且仅当\(n\leq m\leq n+k-1\)。你发现如果上一轮剩下\([l,r]\)个人，那么我们需要在这里面找一些\(k\)的倍数，然后把它们的区间拼起来。这些区间恰好连了起来，于是我们只需要找到其中最小的和最大的\(k\)的倍数。结束了?

AGC020C : 看起来很困难，因为这个子集和的数量很多。

二分答案，然后看有多少子集和不超过mid。这个没法做，因为子集和的数量很多，并且这个计数也很困难。

诶说到计数，这看起来是经典问题。每个位置相当于是\(1+z^{a_i}\)，全都乘起来就好了，可以ln一下再exp回去，这个ln的复杂度非常经典，总之就是\(v^2\log v\)这样的。呃你问ln-exp怎么跑4e6?说实话真的可以。

然后我们直接前缀和，看哪个位置等于\(2^{n-1}\)，当然是取膜的。呃你发现不对，因为一个数可能出现多次/hanx

想不动了。牛逼题!

考虑一个牛逼想法，你发现如果存在一个和为\(x\)的，对称的就有一个\(s-x\)，于是中位数必然是\(\frac{s}{2}\)以内最大的子集和。然后就变成了可行性，bitset冲就行了。

AGC020D : 这个构造看起来是显然的。我们肯定先放A…..样例表示这不对。

先假设\(a>b\)。

考虑我们把这个序列分成\(k\)段，每一段都是A…AB…B这样的。那么显然是\(a\)决定了最长连续段的长度，于是我们假设最长连续段长度是\(l\)，显然是先把A往左填，B往右填，填满了\(l\)个就放上一个另一个字符。

你发现\(l\)应该是\(\frac{a}{b}\)，因为我们可以强行构造 : 放\(b\)段，每一段有一个B，然后强行放A，但是这并不是最优的，因为有样例2。

\(k\)呢?如果我们知道了最优的\(k\)，可以从\(k\)个AB开始，把剩下的AB塞进去，也就是把A尽可能往左塞，\(B\)尽可能往右。

注意到这个塞的过程很有意思，你发现最优的\(k\)必然是最小的\(k\)，因为我们会希望B出现的尽可能往后，于是就不希望在一开始的ABABABAB上消耗太多的A使得B往前。同时，刚才我们给了一个强行构造，这告诉我们\(b\)段一定是可行的，同时可行的又很可能是一个区间，于是我们就从\(b\)出发往下二分即可。

如果\(a<b\)，那么\(l\)应该是\(\frac{a}{b}\)，类似可以给出强行构造，于是一样做即可。

最后统计答案的时候，你会发现这个序列的前面一些段是A塞满，中间一段A是\((a-k)\bmod{l-1}\)之类的东西，后面都是\(1\)，而B是相反的。这构成最多三个区间和两个特殊段，二分在哪一段然后强行搞定即可。

AGC020E : 100是什么鬼数据范围/jy

你谷翻译比较奇怪。题意大概是，你可以把一个01串中循环的子串压缩成一个，比如010101可以写成(01x3)这样的，然后这个东西可以当作一个字符继续被压缩，比如010101010101可以写成((01x2)x3)，当然也可以是((01x3)x2)或者(01x6)。

给一个01串，求它所有子集(就是把它当成状态的时候的子集)的压缩方案数总和。\(n\leq 100\)，膜\(998244353\)。

如果没有这个子集，可以直接dp。设\(dp(l,r)\)表示\([l,r]\)的答案，\(g(l,r)\)表示\([l,r]\)压成一个的答案(至少循环两次)，那么转移是

然后如果是对所有子集，发现复杂度瓶颈在于算\(d\)是不是循环节。我们可以把所有这些段都and起来，每一段必须是这个and的子集，然后拿着这个限制递归下去。也就是说，加一维\(S\)表示必须是\(S\)的子集，然后记搜。

这个复杂度为什么对呢?考虑一个简单分析，我们递归三层长度就到了\(12\)以内，所以只需要考虑前两层，这个\(S\)的种类必然是某些东西的and，这个东西可以用三个参数确定(左端点，第一个\(d\)，第二个\(d\))，于是它的状态数不超过\(n^3\)(实际上远低于这个)，于是总复杂度是\(O(n^5+2^{\frac{n}{8}}n^2)\)。

AGC020F : 传世经典。

我们还是考虑一下做法吧。牛逼做法是，别随机实点了，我们把圆切成若干段，然后直接dp。你发现最终答案是一个关于划分段数的有理分式，所以强行状压dp然后拉插求出最高次项系数即可。这个做法非常离谱，不知道它属于ad-hoc还是有什么普适性。

简单做法是，你发现我们只关心这个弧和上个弧是否相交，状压dp它们位置的整数部分，那么我们只需要知道这些位置的小数部分的大小关系。这个看起来非常牛逼!先爆搜它们的顺序即可。

AGC021A : 这个看起来好困难（

如果我们哪一位不贴着了，后面肯定全填\(9\)，于是只需要枚举哪一位开始不贴着就行了。

等等，你发现除非本来就全是\(9\)，否则从第一位开始就必然不贴着了（

AGC021B : 考虑每个点覆盖的区域一定是一个凸多边形。我们跟别的每个点求一下它俩之间的平分线，然后半平面交一下。如果区域是无界的，那么这个区域边上两条射线的夹角决定概率，如果有界那么概率是\(0\)。

然后你发现这个做法太智障了。我们求个凸包，然后每个点只和它在凸包上相邻两个点互相影响。还是求一下那个平分线的夹角，用atan2即可。

AGC021C : 考虑我们按照每一行有多少的限制，尽可能放少的行数。

于是只需要知道上一行是怎么放的。

考虑如果有竖的，我们肯定是把竖的先排满，因为它们总要占空间。然后进行一个结论的猜，我们猜测行长度是偶数的时候这样放肯定不劣，列长度是偶数的时候可以把行列互换。

如果都是奇数的话，我们考虑一点简单情况。比如\(3\times 3\)的时候，我们是可以放两个横着的两个竖着的的。

猜测留出边上的三行三列，在角上尝试摆一个这个东西，就做完了。实际上根据题解可知它似乎确实做完了。

AGC021D : 这个复杂度看起来很高。

考虑问题出在哪，你发现如果是反转的话，我们在正串上走啥事没有，但是反串上就比较困难，因为我们不知道前面怎么改的。我们需要什么东西来转化这个lcs。

一个串和它的反转的lcs是什么呢?看起来是一个最长的串，使得它和它的反转都在原串中出现过。这好像没啥用。

想不动了。题解表示，牛逼结论是，一个串和它的反转的lcs长度，就是它的最长回文子序列的长度。

考虑怎么用这个结论。要求最长回文子序列，我们只需要枚举回文中心，然后看接下来怎么选。设\(dp(i,j,k)\)表示当前最外面配对的是\(i\)和\(j\)，用了\(k\)次操作，得到的最大长度，那么我们可以枚举上一次选了什么来转移。复杂度\(O(n^5)\)。

注意到这是一个二维前缀\(\max\)，直接前缀和优化，复杂度\(O(n^3)\)。

AGC021E : 又是数数题。

一眼看上去每个方案好像可以任意重排，不过想了想你发现不行，因为只有一种比另一种多的时候才会变色，相等的时候并不会变色。

考虑什么样的方案是可行的。贪心地，我们肯定是希望让每个变色龙先吃红球变红，然后可以给它塞蓝球。如果一个变色龙不得不被塞了蓝球，接下来就需要多一个的红球来把它变红，显然我们希望这样的变色龙没有最好，有也只有一个。

也就是说，如果什么时候蓝球比红球多了，我们就钦点一个幸运变色龙，比如\(1\)号，把多出来的都吃了，最后给它喂上红的。

但是这个看起来还是不是很具体……考虑我们每次拿到一个红球，就把它优先喂给\(1\)之外且还没吃任何球的变色龙。每次拿到一个蓝球，优先喂给\(1\)之外只吃了一个红球的变色龙。如果优先的不存在，那就统统喂给\(1\)。这听起来很对?

所以可以开始dp了，设\(dp(i,j,k,l,0/1)\)表示考虑前\(i\)个球，\(1\)之外有\(j\)个变色龙吃了一个红球，\(k\)个吃了一红一蓝，\(1\)吃的红球和蓝球的差是\(l\)，并且\(1\)现在是蓝色/红色的方案数。复杂度\(O(n^4)\)，玩个锤子!

肯定是这个判定方法不够强，考虑还能不能更强一点。

设有\(a,b\)个红，蓝球，那么最后\(1\)总是吃了\(a-n+1\)个红球，而它吃了多少蓝球，取决于别的变色龙帮它扛了多少蓝球。每一只变色龙上红蓝球的抵消实际上是某种配对，也就是我们取出一个红球和后面的一个蓝球配对。如果我们尽可能多配对，可以配出\(c\)对，那么\(1\)就只吃了\(b-c\)个蓝球。注意到因为我们不能继续配对了，\(1\)一定是先吃了一堆蓝球，再吃了一堆红球，所以可行当且仅当\(a-n+1>b-c\)，也即\(c>b-a+n-1\)。

所以问题变成了求有多少方案使得

• 至少有\(n\)个红球

• 可以配出至少\(b-a+n\)对

。这个咋算?

考虑这个等价于说不能配对的蓝球不能超过\(n-a\)个，于是我们可以考虑什么情况下一个蓝球可以和前面的一个红球配对，你发现把红球看成\(1\)，蓝球看成\(-1\)，那么考察最小的前缀和，这个位置必然是一个蓝球(或者是在\(0\))，而由于它是最小的，前面不可能还有没配对的红球了。所以如果最小前缀和比\(-(n-a)=a-n\)要小，那就没救了，否则有救。

如果你是格路计数大师，那么你已经秒了。这个直接翻折即可，最后效果是两个组合数的差，直接枚举\(a\)算就行了。

将会专门整理折线和翻折法的相关内容。

AGC021F : 还是数数题。看起来数数题较多地达到了agc EF难度（

很难不是dp。

要算本质不同的棋盘个数，直接想法是对三个序列进行dp。这个等价于说，定义一个1是有效的，当且仅当它对三个序列有贡献，而两个棋盘本质不同，等价于它们只保留有效位置之后不同。

考虑我们肯定是从左往右扫，一列一列决策。因为横向只有一个信息，而纵向有两个，大方向上的信息往往难处理，所以我们确实应该从左往右扫，把信息较少的一边留给大方向。

然后考虑如何转移。填空的话考虑了很久，并不是很有前途，于是我们考虑插入，在一行出现第一个1的时候把它插入进状态。设\(dp(i,j)\)表示有\(i\)列\(j\)行(，每行都已经有1)的方案数，枚举填了\(k\)个有效1，那么\(dp(i,j)\)可以从\(dp(i-1,...)\)转移过来，用组合数选一选就行了。统计答案的话，就枚举哪些行没有1，组合数选一选。

但是因为一个有效1不一定会让行数增加(或者说减少)，这样写出来的式子会比较繁琐(一项多次转移)，于是我们定义行有效1说的是对行有贡献的1，考虑枚举行有效1的个数\(k\)来转移。

如果这一行有\(k\)个行有效1，那么有\(k,k+1,k+2\)之一的有效1，因为可能有最多两个列有效1不是行有效的。我们考虑

• 如果有\(k\)个有效1，那么我们只需要把它们都选出来，方案数是\(\binom{j+k}{j}\)。

• 如果有\(k+1\)个有效1，其中多出来的一个就是列有效而不行有效的，我们假设它是最上边的，枚举它在哪，可以得到\(\sum\limits_{l=1}^j\binom{l-1+k}{l-1}\)，根据平行求和我们知道它就是\(\binom{j+k}{j-1}\)，因为它也可能是最下边的，还需要乘一个\(2\)。注意到如果\(k=0\)，我们不应该乘这个\(2\)。

• 如果有\(k+2\)个有效1，其中多出来的两个就是列有效而不行有效的，我们枚举它们的间隔，可以得到\(\sum\limits_{l=1}^{j-1}(j-l)\binom{l-1+k}{l-1}\)。

直接预处理最后这个式子，然后刷表，看起来是\(O(n^2m)\)(，并且还有小问题)。

为了进一步优化，最后这个式子怎么化简?

首先我们把那个\(j-l\)换成binom，那么它就是\(\sum\limits_{l=1}^j\binom{j-l}{1}\binom{l+k-1}{k}\)。这个让我们想起来一个经典式子是\(\sum\limits_{-r\leq k\leq l}\binom{l-k}{m}\binom{r+k}{n}=\binom{l+r+1}{m+n+1}\)。但是这个sigma的范围不是很对，不过没关系的，因为\(l<1\)的时候第二个binom永远是\(0\)。于是有\(\sum_\limits{l=1}^j\binom{j-l}{1}\binom{l+k-1}{k}=\binom{j+k}{k+2}=\binom{j+k}{j-2}\)。这玩意形式怎么这么简单?这让我们不禁怀疑是不是算错了，不过事实上没有算错。

三个东西加起来，也就是\(\binom{j+k}{j}+2\binom{j+k}{j-1}+\binom{j+k}{j-2}=\binom{j+k+1}{j}+\binom{j+k+1}{j-1}=\binom{j+k+2}{j}\)。我们前面也讨论了，如果\(k=0\)，这个方案数应该是\(1+j+\binom{j}{2}\)。

然后这个东西看起来像是带项式技巧，于是我们需要把这个式子改成填表的式子(，而不是刷表的)。转移是\(\left(1+j+\binom{j}{2}\right)dp(i,j)\rightarrow dp(i+1,j),\binom{j+k+2}{j}dp(i,j)\rightarrow dp(i+1,j+k)\)，于是第一个照抄，第二个把\(j\)换成\(j-k\)，我们知道

。然后忽略第一项，强行把\(k=1\)改成\(k=0\)，差值我们转移完一层之后补上。于是拆开之后得到

这是\(\frac{dp(i-1,j)}{j!}\)和\(\frac{1}{(k+2)!}\)的卷积，于是法法塔就行了。复杂度\(O(nm\log n)\)。

也有微分方程做法，但是那个在这里不如法法塔优秀。

AGC022A : 感觉上随手，但是想了想好像并不能直接开始写（

考虑如果字典序不比zxywvutsrqponmlkjihgfedcba小，那就没救了。如果有救，我们显然从前往后贪心，用同样的方法判断填了这个之后还有没有解即可。

AGC022B : \(n\)有足足2e4，而值域只有3e4，这就很离奇。也就是说平均每三个数我们就需要选择两个数。

\(\gcd(a_i,S-a_i)\neq 1\)是个啥?注意到\(\gcd(a_i,s-a_i)=\gcd(a_i,s)\)。这就非常好?

为了满足这个限制，我们显然的想法是让所有数都有一个公因数，但是第一个限制就告诉我们不能这样做，同时值域也不允许我们这么做。

考虑我们让所有数的和具有两个因数，而剩下的数都具有这两个因数中至少一个。显然我们希望选择\(2,3\)两个数，也就是说我们希望和是\(6\)的倍数。注意到\(2,3\)中至少一个的倍数的密度恰好是\(\frac{2}{3}\)。

于是我们要怎么调节，使得和总是\(6\)的倍数呢?\(2,3\)中至少一个的倍数，膜\(6\)的值是\(0,2,3,4\)之一，于是为了整体互质首先我们可以放\(2,4,3,9\)四个数，然后放\(2,4\)，放\(3,3\)，用\(0\)调节奇偶性。\(n=20000\)我们恰好可以解决，但是现在问题是\(n=3\)。

不需要思考了，把样例copy上去就行了（

AGC022C : \(n,v\leq 50\)/jy

这数据范围太离谱了。我们考虑\(a_i\)可以如何变成\(b_i\)，它显然是膜若干个依次递减的数，并且其个数不超过\(\log\)个，因为每次取模都会减半。然后我们只需要从大到小膜这些数就行了。

注意到每个\(k\)只会用一次，于是我们肯定希望尽量少用大的，于是考虑从大到小贪心，考虑当前这个操作数是不是必须的，这个可以直接dp搞定。复杂度可能居然是多项式的（

AGC022D : 怎么D已经是黑色了（

考虑使用撞墙的次数描述一个方案的代价，也许这应该在思考的过程中发现，不过我懒得写那么长（

为了方便讨论，先给每个\(t_i\)膜\(2L\)并把商加入答案。

考虑我们总要等火车，并且火车来了的时候跟着走必然不劣。进来的时候和出去的时候只有四种情况，并且要么撞墙一次要么撞墙两次 :

• 从左边来，往左边走，当且仅当\(t_i\leq 2(L-x_i)\)，撞墙一次。

• 从左边来，往右边走，当且仅当\(2(L-x_i)<t_i\)，撞墙两次。

• 从右边来，往左边走，当且仅当\(2x_i<t_i\)，撞墙两次。

• 从右边来，往右边走，当且仅当\(t_i\leq 2x_i\)，撞墙一次。

那么可以考虑到每个商场有四种可能 :

• 必然往左边走，当且仅当\(2x_i<t_i\leq 2(L-x_i)\)，如果从左边进入则只需要一次撞墙就可以出去。

• 必然往右边走，当且仅当\(2(L-x_i)<t_i\leq 2x_i\)，如果从右边进入则只需要一次撞墙就可以出去。

• 往来时的方向走，当且仅当\(t_i\leq 2\min(x_i,L-x_i)\)，总是需要两次撞墙才能出去。

• 沿来时的方向走，当且仅当\(2\max(x_i,L-x_i)<t_i\)，总是只需要一次撞墙就可以出去。

第四类点啥用也没有，直接每个给答案加\(2L\)就行了。如果往右走走到一个一类点，或者往左走走到一个二类点则可以减小答案，而往右走必然是从二类点或者三类点出发，于是每个点拆成出入，这看起来就是说二三类出点可以匹配一类入点，一三类出点可以匹配二类入点，匹配一下就行了。说不定可以跑过（

考虑如何优化。注意到一类点只可能在左半边，二类点只可能在右半边，所以一二类点不可能匹配。于是只可能是三类点匹配一二类点，把左右分开，以左半边为例，从左往右扫，维护还没匹配的三类点，遇到一个一类点则找到前面第一个还没匹配的三类点和它匹配，意思是走完这个点之后走到那个三类点去。

• Previous
  模拟费用流
• Next
  省队胡策