二轮省集

再次来到宇宙中心曹县所在的省份参加省队集训。

Day1

模拟赛

T1 麻将

给一个01串，求最短的没有作为子串出现过的01串，多解输出字典序最小的。$n\leq 2^{24}$，0.2s。

省选计划原题（

考虑答案长度不会超过$24$，从大到小枚举答案，问题变成求长$k$子串的$\mathrm{mex}$，维护一个值域bool数组表示每种子串是否存在就好了。你发现长$k$的只有$2^k$种，所以就$O(n)$了。

T2 德州扑克

平面上有一些线段，每次给一个横平竖直的矩形，查矩形内的线段长度除以总线段长度。保证任意两条线段不交，并且每条线段不是横平竖直的。$n,q\leq 10^5$，2s。

首先可以把矩形差分掉，问题变成求一个点左下方的线段长度。

先只考虑斜率为正的线段，负的可以反着跑。可以发现固定一个查询点的话，有贡献的线段只有三种 :

完全在查询点左下方的
穿过上边界的
穿过右边界的

第一种可以直接转成二维数点，第二种和第三种类似，只考虑第三种。

扫描线。从左往右扫过平面，用平衡树维护线段。不相交就非常好!

考虑扫描线右移的变化量，发现每条线段的变化量是一样的，所以相当于要平衡树支持全局带系数加，查询区间和。直接做就好了。

复杂度$O(n\log n)$。

T3 将棋

给一棵树，边有边权，每次给一个点集，查询这个点集的斯坦呐树上，有多少种方案选择两条不同的边，使它们边权相同。$(a,b),(b,a)$看作同一种方案。$n,q\leq 10^5$，2s。

不管怎么着，先想想有没有单次询问只关于点集大小的做法。考虑这个斯坦呐树可以拆分成若干链，条数是线性的。每条链内部可以括号序莫队搞定，链之间可以差分成到根的四条链之间的贡献，也可以莫队搞定。现在问题是链之间贡献次数是平方级别。

考虑进行根号分治，点集大小很大的时候$O(n)$暴力，小的时候用上面的算法，取阀值$\Theta(n^{\frac{1}{3}})$，复杂度可以搞到$O(n^{\frac{5}{3}})$。当然认为$n,m$同阶。

另一个做法是，继续对颜色出现次数根号分治来代替上面链之间的莫队，然后就可以做到$O(n\sqrt{n}\log n)$了!

啊具体就是，把颜色分成大颜色和小颜色。大颜色数量很少可以预处理前缀和然后直接查，小颜色可以枚举一对考虑贡献，发现如果$(u,v)$同是一个小颜色，那么两条到根的链之间有贡献，当且仅当它们的端点分别在$u,v$的子树中。然后子树是dfn的区间，所以就变成了矩形$+1$单点查询。

然后对查询也修改根号分治的阀值到$\Theta(\sqrt{n})$，就相当于是$O(n\sqrt{n})$次矩形$+1$和单点查询，直接扫描线，复杂度是$O(n\sqrt{n}\log n)$。啊你问为什么是$O(n\sqrt{n})$，而不是$O(n^2)$?这当然也是琴生不等式搞出来的。

好像可以把$\log$放到根号下面，但是我不会/cy

讲课

分治数据结构。

区间的笛卡尔积是矩形，换句话说如果看到一个东西有贡献，当且仅当查询区间左右端点分别在两个区间内，就可以想到$(l,r)$应该在这两个区间的笛卡尔积内，所以就可以上二维数点。

EC Final2020 G

给一个序列，每次给一个区间，查询多少子区间颜色数是奇数。

这个东西等于，区间所有子区间颜色数膜$2$的和。

扫描线。考虑插入$i$的时候，只有左端点在$[pre_i+1,i]$这一段区间的询问会多出来$a_i$这种颜色，所以相当于区间异或，查询区间历史和，搞就是了。

神必题

神必题讲啥啊（

JOISC2021 饮食区

有一排队列，支持区间连续push/pop $k$次，如果pop超了那就直接pop空，查询某个队列里第$k$个数。

先把这个pop干掉，做法是直接求出每次查询查的是不考虑pop的第几个数，毕竟队列是一个数组和head tail，这个的意思就是直接求出数组上的下标。问题在于队列中数的个数可能不够，于是维护数的个数，需要支持区间加减，区间对$0$取$\max$，吉老师线段树就结束了。

扫描线扫序列，数据结构维护时间。发现一次区间push会在左端点被激活，在右端点右边被不激活，也就是两次单点修改。然后要支持查kth，在时间上建线段树就行了。

hdu5118 GRE Words Once More!

给一个DAG，点从$1$到$n$标号；有一些点是被标记的。每次查询一个$k$，求从点$1$开始、截止于一个被标记结点的路径中，编号字典序第$k$小的路径长度。$n\leq 10^5,k\leq 10^{18}$。

图剖!好像写过来着。

另一种做法是可持久化平衡树，它支持$O(\log\text{结点数})$的复制、拼接。

考虑拓扑排序，每一个点$u$维护一个序列表示给定$k$，kth路径会是什么。

假设$u$是标记点，$k=1$就是不走，$k=2,...,size(\text{第一个邻接点}+1)$就是接上第一个邻接点的序列$+1$，后面类似。

发现可以用可持久化平衡树支持复制。但是路径数量是指数级的，会爆掉，不过发现$k$只有1e18，我们可以在$k$之后截断，复杂度就是$O(n\log v)$。

luogu6617 查找

给一个序列和常数$w$，支持单点修改，查询区间有没有两个数和为$w$。$n,q\leq 5\times 10^5$，4s。

对于每个数，维护它前面最近的和它和为$w$的位置$pre$。问题变成查询区间$pre$有没有在区间内的，线段树维护$pre$的最大值即可。

不过修改的时候可能会影响一堆后面的位置，比如有一排$x$，前面是一个$w-x$。

不过发现这些$x$除了第一个都没有用，所以我们可以改为只维护第一个，这样变化量就变成$O(1)$了。

爆炸oj3489

序列，每次查询一个区间中只出现过一次的数中最大的。

每个位置$i$的贡献就是$l\in[pre_i,i],r\in[i,suc_i]$，这是一个平面上的矩形。

考虑离线怎么做。扫描线扫序列(等价于从左往右扫平面)，那就是要支持区间插入一个数，区间删除一个数，单点查$\max$，可以用线段树套堆。

在线的话就是可持久化一下嘛……你发现可持久化整个树套树有点恶心，不过这里只需要可持久化下来那个堆的堆顶，所以就非常简单了!

Ynoi2007 rgxsxrs(Range Greater than x Sub x/ Range Sum?)

给一个序列，支持区间$>x$的减$x$，查询区间和/$\min$/$\max$。$n,q\leq 5\times 10^5,1\leq x,a_i\leq 10^9$，6s。

肯定要搞这个值域，但是怎么搞呢?

考虑一个类似于基数堆的做法，我们把值域分成$\log v$块，也就是$[0,1),[1,2),[2,4),...$这样分。

考虑如果要减$x$，对于$2^k>x$的所有块$k$都会减，$2^{k+1}\leq x$的都不变，$2^k\leq x<2^{k+1}$的最大的若干个会被减。

容易想到用块编号的减小摊掉爆力减的复杂度。第一种可以打上标记并爆力处理最小的若干个的块编号变化，第二种不管，第三种发现每次被减都会让块编号变小，所以也可以爆力。每一块开一棵平衡树维护即可，复杂度$O(n\log n\log v)$。

当然平衡树常数太**大了，我们可以换成线段树，存在某种神秘方法让它跑得飞快，不过我不会/cy

loj6276

树，点权，问有多少链满足链上颜色互不相同。每种颜色出现次数不超过$20$，$n\leq 10^5$，4s。

对每个颜色分开考虑。考虑对于两个同色点$u,v$，如果它们不是祖孙关系，那么相当于限制路径的两个端点不能分别在这两个子树里。可以相当转成计算不满足的方案数，于是如果全没有祖孙关系，就可以直接矩形面积并。

呃如果有怎么搞?发现在祖先那里会变成一个子树外，而子树外是两个区间，所以相当于两个矩形，做就行了。复杂度$O(nk\log n)$，当然$k=20$是最大出现次数。

啊你说为什么不是$O(nk^2\log n)$?发现我们可以用$k$个点产生$O(k^2)$个矩形，而$k^2$是下凸函数，所以琴生不等式一下你就知道每次查询都取满是复杂度上限，此时就只有$\frac{n}{k}$个颜色。这部分分析非常重要，这题$k^2$不是很大，但是有的题里面$\sqrt{n}^2$就很大了/jy

Ynoi2008 rdCcot/thuwc2020 某科学的动态仙人掌

树，距离是边数，还有一个常数$C$。

对于一个树上点集，定义其中两个点$u,v$是$C$-连通的，当且仅当可以只走点集中的点，每一步距离不超过$C$，从$u$走到$v$。

每次给一个编号区间，查询有多少$C$-连通块。$n,q\leq 10^5$。

连通块计数问题，考虑对每个连通块找一个代表元。容易想到随便找一个根，然后选择最浅的点作为代表元，不过这个不一定唯一。

不管怎么说我们先接着往下考虑一下。一个点是连通块最浅的点之一，当且仅当比它浅的所有点，距离它$>C$。这个看起来还挺简单?

定义邻域$\mathrm{N}(u,d)$，$k$级祖先$\mathrm{LA}(u,k)$，然后我们可以转化成 : $\mathrm{N}(\mathrm{LA}(u,\frac{C}{2}),\frac{C}{2})$中没有点在查询区间内。

呃这里看起来需要对奇偶性分类。

如果$C$是奇数，应该是$\mathrm{N}(\mathrm{LA}(u,\frac{C+1}{2}),\frac{C-1}{2})$。
如果$C$是偶数，应该是$\mathrm{N}(\mathrm{LA}(u,\frac{C}{2}),\frac{C}{2}-1)\cup\mathrm{N}(\mathrm{LA}(u,\frac{C}{2}+1),\frac{C}{2}-1)$。

然后，没有点在查询区间内，我们可以求出这个邻域内的编号前驱后继，如果查询区间不包含前驱后继，那么这个点就是最浅点之一。

要把多个最浅的点去重，首先注意到最浅的点深度都相同。然后考虑，两个深度相同的点$C$-连通，当且仅当它们的$\lfloor\frac{C}{2}\rfloor$级祖先相同，这个是显然的。这就非常好，于是可以利用它来去重。

预处理的时候，先对每个深度按照$\lfloor\frac{C}{2}\rfloor$级祖先划分成若干等价类。然后对于每个元素，找到刚才说的前驱后继，那么$x$的贡献就是一个矩形；去重那就对每个等价类求矩形并。

一般的矩形并是不容易用若干不交矩形简单地表示的，但是这个矩形并很特殊。区间包含一个点的限制是$y=x$上一个点的左上方，不包含前驱后继的限制是$y=x$上方一个点的右下方，画一画你发现如果不考虑不包含前驱后继的限制那么可以直接处理出来，而对于前驱后继的限制，每$k$个点共用一组前驱后继都会多出来$O(k)$个矩形，于是划分中的矩形数确实是线性的。现在我们可以扫描线扫一扫了。

但是怎么求邻域前驱后继?考虑它是可快速合并的，这个合并就是$\min/\max$，所以它是幂等的。点分治，容易做到$O(n\log^2 n)$。

呃但是这太慢了。怎么优化?

考虑每一层的问题相当于把点按深度拍成序列，每次查询一个前缀的前驱后继，容易想到时间倒流之后用链表维护。但是这个不是很行，因为我们查询的数不一定也在这个序列中，这就会导致奇怪的问题。

并查集。

不过要排序，这个可以点分治过程中归并(，这要求我们用二路合并的分治结构，可以用每次合并两棵最小的子树的trick，或者直接换成边分治)。这样做复杂度就是$O(n\log n\alpha(n)+q\log n)$。

科技 : 如果知道合并的顺序，可以按$\log$大小分块，把并查集做到线性。所以可以当我们做到了$O((n+q)\log n)$。

uoj207 共价大爷游长沙

动态树(而不是森林，也就是说每次操作是cut之后link)，支持插入、删除链，查询一条边是不是在所有链上。

LCT。考虑一条边可行，相当于较深的点的子树中，包含了所有链的恰好一个端点。

你发现相当于一条链出现两个端点或者不出现端点就不行，出现一个就可以，于是我们可以用一个$\operatorname{xor}$来解决这个问题。

这里有一个经典trick是$\operatorname{xor}$哈希。给每条链随机一个巨大权值，如果是unsigned long long的话据说错误概率低于$\frac{1}{10^9}$。

然后就LCT维护子树$\operatorname{xor}$和了。

链排序

树，点权。每次给两条长度相同的链，把两条链分别拿出点权排序，输出哪些位置不同，当然这个排序不会真的排。保证一共输出不超过$10^6$个数。

考虑hash+二分，用可持久化值域线段树维护到根的hash值，然后链hash值可以用这个硬拼出来，于是可以二分找到第一个不同的位置，然后继续二分下一个位置就行了……听起来就真**离谱。复杂度居然还是一个$\log$。

Ynoi2008 stcm(Set, Tree, Cancel & Modify?)

给你一个集合，支持插入一个点和撤销，构造一个方案，凑出每一个点的子树补。子树补就是子树之外的点。$n\leq 10^5$，插入次数$4.5\times 10^6$。

考虑菊花怎么做，发现此时子树就是自己，删掉每一个求剩下的，容易想到分治。

考虑原问题怎么做，进行重链剖分，然后类似于菊花，只不过从一个点递归到一些点变成了一条链递归到一些链。考虑用类似于静态Top tree的方法，把我们的分治树换成Huffman树，就一个$\log$了。

这本质上是静态Top tree上的消失之物。

Day2

模拟赛

题面很好玩（

T1 多项式时间哈密顿回路

给一个外向基环树森林，每一个点上有若干个物品，物品可以沿着有向边移动，你可以往任意结点放共$m$个物品，构造方案使得所有点上物品数量最小值最大，只需要输出这个最大值。$n\leq 10^5,m,a_i\leq 10^9$。

直接二分答案，基环树dp。

T2 AI高考数学134分

给三个序列$a,b,c$，对于每个区间，对$a,b,c$中这个区间分别求极差，然后乘起来作为这个区间的权值。求所有区间的权值和。$n\leq 10^5$。

枚举右端点，搞三个单调栈，然后可以用线段树维护所有东西来处理。

啊你说具体维护什么?需要

三个序列的极差$x,y,z$，
$xy,yz,xz$，
$xyz$。

转移可以写成矩乘，做就是了。当然矩乘比较慢，可以神秘打标记。

T3 自动化leetcode

给一个序列$a$，每次查询给出一个区间和一个数$x$，问从左往右扫过这个区间，每次把$x$变成$\vert x-a_i\vert$，最后会得到什么。$n,q\leq 10^5,a_i,x\leq 10^7$。

std倒是依赖值域……不过是在可持久化平衡树建树的时候。

容易发现段数是指数级，于是要想直接维护这个东西，可以想到可持久化平衡树。

考虑全局询问怎么做。从左往右扫过序列，一开始平衡树存储恒等变换，然后每次相当于把$a_i$上面的部分移下来，下面的部分翻转一下。你发现这两部分出现了重合!这就让我们不是很好维护。

考虑倒过来做，你发现正着相当于给$x$求$f(x)=\vert x-a\vert$，倒着相当于给$f(x)$求$x$，解一下你知道当$x\geq a$的时候是$x=f(x)+a$，否则$x=-f(x)+a$。第一个意义是把整个平移$a$，第二个是把$a$以下翻转，这俩正好是不交的。于是可持久化平衡树硬上就好了。

要支持区间查询，可以在外面套一棵线段树。$O(n\log n\log v)$。

除此之外，这个题合并的时候也可以用第二分块的trick，复杂度是$O(n\sqrt{v})$，不刻意卡的话可以冲过去。

讲课

CF464E The Classic Problem

每条边边权是$2^{w_i}$，求最短路。

考虑Dij只需要支持

一个数加上一个边权
比较两个数
一个数赋值成另一个数

看到第三个，考虑可持久化数据结构。我们选择可持久化线段树。

加一个边权，可以二分出进位的一段做推平，然后对前面那一位单点修改。

比较两个数，相当于比较字典序，可以用二分哈希来搞定。

CF1446D2 Frequency Problem 加强版

序列，求一个最长的子段，使得其中众数不唯一。$n\leq 5\times 10^6$。

当然还是那个结论，答案区间中一定有一个众数是全局众数。

考虑找到所有的全局众数，然后如果全局众数不唯一就做完了，否则对于每个数，尝试找到最长的区间，使得这个数和全局众数出现次数相同。注意这样找到的区间不一定满足它俩是众数，但是它的正确性在于这样找不优于答案，并且一定会找到答案。

考虑怎么让复杂度只跟我们处理的这个数出现次数$cnt$相关。

进行两轮标记。第一轮一开始把所有全局众数标记成没用的，然后对于每个我们处理的数，从它往左找到第一个没用的全局众数，把它改成有用的。第二轮反过来往右找没用的位置，如果一个位置两轮都没被标记成有用的，那它确实没用了。这个好像有点像雪灾与外卖的某个部分分?

怎么证明这个东西的正确性?如果一个全局众数在第一轮被标记没用，那么它往右不管怎么延伸，都有全局众数出现次数多于我们处理的数(因为数两两配对，而总是剩下这一个)，所以它不可能作为一个左端点。

然后剩下的可能端点数就是$O(cnt)$的了。不过怎么找到这些点?

数据结构问题是 : 删一个数，查询前驱，重置。可以用并查集来维护，当然可以用线性并查集做到线性。

啊你说重置?考虑线性并查集需要修改$\Omega(\log n)$次才会合并第一次，所以全撤回去复杂度是正确的。普通的并查集呢?好像只能多个$\log$吧。

然后问题是在这些端点里面找到最长的区间，使得全局众数和我们处理的数出现次数相同。

这是经典技巧。把所有全局众数改成$1$，处理的数改成$-1$，问题变成找和为$0$的区间，拆前缀和扔进桶里即可。这样就线性了。

CF997E Good Subsegments

给一个排列，每次给一个区间，查询有多少子区间值域连续。$n\leq 1.2\times 10^5$，可以做到$5\times 10^5$。

你发现因为是排列，一个区间连续，相当于$r-l=\max-\min$。

考虑分别建立大/小根笛卡尔树，那么每一个$\max/\min$的贡献是一个矩形，同时$l,r$的贡献也是矩形。问题变成矩形加减，数一个点右下方有多少$0$。

先把修改查询都差分掉，然后肯定扫描线，问题变成区间加减，查历史$0$总个数。怎么维护$0$的个数?

你发现这里一定有$r-l\leq\max-\min$，所以我们可以线段树维护区间最小值和最小值个数，然后历史和的话硬打标记就好了。

CF765F Souvenirs

给一个序列，每次查询一个区间中选两个数，差的绝对值的最小值。$n\leq 5\times 10^5$。

回滚莫队大家都会!但是那太慢了。

对于每个$i$，考虑它和哪些位置拼起来可能有用，我们试图从左往右找出这些位置。

先只考虑顺序对，逆序对可以相反地求出来。

我们找到$i$右边第一个比$a_i$大的$a_j$，这个$j$肯定有用。然后考虑接下来如果一个$k$想要$(i,k)$优于$(i,j),(j,k)$，那么$a_k$就必须更靠近$a_i$(比起它靠近$a_j$的程度)，那么$a_k$的取值范围就在$[a_i,\frac{a_i+a_j}{2}]$内了。你发现值域变成了一半!这样找$O(\log v)$个就一定会停下。

这个东西可以从后往前建立主席树来找到，每次是一个$\log$的。剩下的就是二维数点了。总共是$O(n\log n\log v+m(\log n+\log\log v))$，不过$\log\log v$太没用了可以扔了（

CF176E Archaeology

维护一个点集，支持插入删除，查询斯坦呐树权值和。$n,q\leq 10^5$。

呃结论是，斯坦呐树权值和，就是按照dfn排序成一个环之后，相邻点两两距离之和的一半。set维护即可。

另一种做法是Top tree/jy

不过可以比Top tree更优，因为我们可以用vEB代替set查前驱后继。

CF896E Welcome home, Chtholly

第二分块的在线版。

给一个序列，支持区间$>x$的减$x$，查询区间某个数出现次数。$n,a_i\leq 10^5$。

值域1e5!要查询出现次数，显然是开值域桶。要平衡掉巨大的桶，考虑~~动态开点线段树~~分块。

容易发现对于这个修改操作，每一个数大小都是不升的。这题核心在于 : 用块最大值的减小，摊掉爆力修改的复杂度。

先考虑我们需要支持什么查询。整块查询的时候，只需要查一个数出现次数；零散块重构的时候，则需要快速对于每个数查询它变成了什么数。

考虑设最大值是$k$，

如果$2x> k$，那么最大值会减小至少$k-x$，所以我们只可以付出$O(k-x)$的实际复杂度。啊这个很简单，爆力枚举所有被减了的$O(k-x)$个值，然后用并查集来合并就好了。啊具体就是我们需要合并$i$和$i-x$。
如果$2x\leq k$，那么最大值会减小至少$x$，所以我们只可以付出$O(x)$的实际复杂度。考虑反过来，我们把所有值都减$x$，然后把原来$1,...,x$这些值都加上$x$，第一个可以打全局减标记，第二个可以枚举这$O(x)$个值用并查集合并。

注意到这个并查集比较特殊，它的find一定是在零散块重构的时候，所以一定总是find一遍，所以复杂度是线性的。总共就是$O(n\sqrt{n})$。

离线版本是线性空间的，这个注意到查询很容易合并，所以可以离线对于每一块分别处理。

CF700D Huffman Coding on Segment

给一个字符串，每次查询区间Huffman编码之后的长度。$n,q\leq 10^5$。

出现次数只有根号种，可以暴力莫队搞定每个区间的出现次数们。然后直接线性Huffman树好像多$\log$……

考虑两个优化 :

对于权值相同的字符，它们没有区别，我们可以批量处理。用一个pair记录权值和权值出现次数$(k,c)$，然后每次拿出$k$最小的pair，先内部批量合并一轮(变成$(2k,\lfloor\frac{c}{2}\rfloor)$)。如果是奇数个再去找次小的，从次小的里面拿出一个，和内部合并剩下的一个配对。
因为上面说的出现次数最大只有$n$，可以开一个桶维护每个出现次数的字符个数，这样可以快速搞定内部合并一轮时贡献到$2k$的问题，使得每个$k$只有最多一个pair。

然后复杂度分析也很简单。考虑我们每次合并都会使最小的$k$增加至少$1$(因为最小的$k$也最多只有一个pair)，所以合并根号次就会让最小值达到根号。接下来因为权值和(出现次数和)是$O(n)$的，那么最多还剩根号个元素(现在权值相同的算多个)，每次合并都会减少至少一个，所以合并根号次就没了。这样就是一个根号。

CF453E Little Pony and Lord Tirek

给一个序列，每个位置一开始是$a_i$，每时刻会增大$r_i$，直到上限$m_i$。有一些操作依次进行，每次查询一个区间的和，并把这个区间推平成$0$。

破坏性查询，考虑连续段均摊，当然这里的连续段是上一次推平时间的连续段。发现查询一整个连续段的时候，我们需要知道的信息有两个 :

所有达到上限的位置的上限之和
所有没有达到上限位置的增长速度之和

第一个怎么做?考虑如果距离上一次推平的时间$t$至少是达到上限所需时间$\lceil\frac{m_i}{r_i}\rceil$的时候，$i$就达到上限了。于是可以用一个按$\lceil\frac{m_i}{r_i}\rceil$排序的平衡树维护。

第二个怎么做?用那个平衡树也可以搞定。所以我们就得到了$O(n\log n)$算法。

CF1476G Minimum Difference

给一个序列，单点修改，或者查询从一个区间中选$k$个不同的数，使得这些数在区间中出现次数的极差最小，输出这个极差。$n,q\leq 10^5$。

不同出现次数是根号的，所以还是可以爆力莫队搞定，单点修改那就带修莫队。就过了/jk

CF1344E Train Tracks

树，边权。树上有一些火车，每个在$t_i$从$1$出发前往$s_i$。每个点每个时刻向儿子的铁轨只能有一个方向，你每个时刻可以选择一个点，更改它连向的儿子，这个操作先于火车移动。如果火车跑到一个点上，接下来要走的方向和铁轨开放的方向不同，那它就会自爆。求能不能让火车不自爆，如果不得不自爆最晚在什么时候自爆，以及至少需要调整多少次铁轨方向。

这个信息看起来很巨量，所以考虑能不能重用。想到静态链分治，数据结构要支持插入并查询前驱后继，用一个set来维护即可。可以换成动态开点vEB，不过我觉得没有人想写动态开点vEB的。

CF1017G The Tree

树。支持把一个点的黑色连通块向下扩展一个单位，把一个点子树染白，查询一个点的颜色。

考虑一个点是黑色，当且仅当存在一个祖先，使得这个祖先到这个点链上染黑的操作次数加起来，至少有这条链这么长。这个可以树剖之后从下往上线段树二分解决，或者直接静态Top tree二分做到一个$\log$。

染白这个操作很不好，因为光是清空子树的染黑操作次数不够，上面的染黑操作可能渗透下来。

不过你发现，如果上面的操作渗透下来$d$单位，我们可以染黑$-d$次。这么做可行是因为染黑这个操作次数已经被我们彻底抽象掉了，它的意义已经不重要了，进行负数次也没什么问题。这个$d$也可以树剖线段树求出来。

CF1340F Nastya and CBS

收录于类楼房重建线段树。（然而好像写错了，不过已经改正

Day3

模拟赛

定义$f(x)$是$x$所有因子的异或和，给一个$n$，求$f(1)$到$f(n)$的异或和。$n\leq 10^{14}$。

直接整除分块。

平面上有一些横平竖直的线段，在两条线段之间连边当且仅当它们有交，求所有割点。

显然主席树优化建图，但是建出来发现不容易直接跑Tarjan。

考虑不要优化建图，而是直接利用主席树的结构来维护Tarjan。我们要支持 :

查询第一个没有走过的邻接点
查询邻接点low的最小值

，显然可以维护

区间有没有没被遍历的点
区间low的最小值

。注意到在主席树上合并信息并不容易，不过其实我们不需要保证所有点的信息都是正确的，可以等需要信息的时候再去push_up。这样每个点应该只被更新一次，所以就是$O(n\log n)$。

另一个做法是，注意到图的特殊性质，只可能是一条横线割掉之后让竖线不连通，或者一条竖线割掉后让横线不连通，可以分开处理。如果只要求一遍连通性的话，直接扫描线扫过去，用线段树维护可以合并的点，并查集来合并就好了。要删每一条竖线，可以用消失之物的分治。这样做是俩$\log$的。

树，每个点有一个颜色，支持单点改颜色，一个点所在的同色连通块改颜色，查询一个点所在同色连通块的颜色、大小、最大深度、最小深度。颜色只有$30$种。

点连通块性质不优秀，把点权转移到父边上，转而维护边连通块。

考虑每次连通块改颜色，可能会使连通块变大，不过这个是有均摊的，可以爆力修改。

ETT。维护连通块下方有哪些颜色，每次改的时候找到下面有没有相同的颜色，爆力递归下去合并就好了，这样我们以一个$\log$的代价合并了两个连通块。总复杂度$O(nc\log n)$，那个$c$是合并颜色是否存在信息的代价。

发现这个有哪些颜色的合并是一个二进制$\mathrm{or}$，考虑压位成一个int，复杂度就砍掉了那个$c$。

讲课

lxl!

Ynoi2016 这是我自己的发明

换根的trick，然后大力差分。

爆炸oj3920 Yunna的礼物

序列，每次给出$x,y$，查询一个区间里面出现次数第$x$小的数里面第$y$小的。线性空间。

不管线性空间怎么做?要查这个出现次数很容易，一个值域分块就好了。要查这个数，我们可以对每种出现次数开一个值域分块，然后动态开点一下就好了。

诶这个动态开点好像是空间瓶颈。考虑可能的$(\text{出现次数},\text{数})$只有$n$种，所以我们可以进行高维离散化。

高维离散化是什么?开一排vector，对于出现了$c$次的$x$，把它分别push进第$1,2,3,...,c$个vector里，然后对于每个vector分别离散化。

然后就很简单了，我们可以直接在每个vector上开值域分块，空间就是线性了。

爆炸oj4241 历史研究 (加强版?)

给一个序列，每次查询一个区间$x\times x\text{的出现次数}$的最大值，线性空间。

这题可以不用回滚莫队。

不考虑空间，爆力做法是莫队的时候直接给每个出现次数开值域分块。不同的出现次数只有根号种，所以可以直接爆力查询每种出现次数的最大值。

注意到跟上一题一样，这题也可以高维离散化，然后再值域分块就好了。

Ynoi2015 いずれその陽は落ちるとしても

给一个序列，每次查询一个区间的所有子序列去重之后的和的和。每次的模数不同。

很有意思。考虑如果区间长度是$l$，一个数$x$出现$c$次，那么它的贡献是$x2^{l-c}(2^c-1)=x2^l-x2^{l-c}$。第一个很容易维护，第二个怎么办?

注意到不同的出现次数只有根号种，所以我们完全可以搞出来爆力处理。

至于快速幂，可以用光速幂来做。

HNOI2016 大数

考虑是质数是个什么东西。

考虑打一个后缀和(因为前缀和不好打)，然后一个区间就可以表示成$\frac{suf_l-suf_{r+1}}{10^{n-r}}$。

显然特判掉$p=2,5$，然后你发现因为$p$和$10$互质，那个除$10^k$是不影响素性的，所以就变成区间数有多少对膜$p$相等，小Z的妹子即可。

luogu3604 美好的每一天

给一个串，每次查询一个区间里有多少子区间可以重排成回文串。

考虑利用异或来搞。给字符$c$权值$2^c$。这样如果一个区间的异或和是一个$2^k$就可行。

于是搞一个前缀和，枚举那个$k$来转移，变成了小z的妹子，复杂度是$O(n\sqrt{n}\Sigma)$。这太慢了!

二次离线。然后就变成$O(n(\sqrt{n}+\Sigma))$了。

线性空间离线区间逆序对

收录于 apio的课。

爆炸oj4358 permu

给一个序列(而不是排列)，每次查询把一个区间所有数扔进一排桶里，得到的最长连续段长度。

考虑对于每个连续段维护左右两个指针。每次插入的时候，如果插入到非空桶那就没啥需要做的，否则我们看左右是不是已经有东西，一边有就并入，两边都有就合并两边。这个不好删除，所以可以回滚。

在线区间逆序对

爆力处理各种贡献就好了!

SHOI2006 Homework

集合，支持插入$x$，或者给出$y$，查询$x\bmod{y}$的最小值。值域$10^5$。

对$y$根号分治。对于小的直接维护答案，对于大的，注意到$y,2y,3y,...$只有根号个，而只有每一个的后面第一个$x$可能产生贡献。

于是要支持$O(\sqrt{n})$插入和$O(1)$查询后继。发现插入就是前驱+推平，所以可以直接值域分块解决。

POI2015 ODW

树，点权，每次给出$u,v,k$，求从$u$出发，每次跳$k$步，跳到$v$，走过的点权和。保证$u,v$的距离是$k$的倍数。

对$k$根号分治。对每个小的$k$离线下来，按深度膜$k$建$k$棵虚树做树上前缀和。

对大的$k$直接爆力跳，用$O(n\log n)-O(1)$ LA的科技就可以做到一个根号了。当然实际上树剖LA非常快。

Ynoi2015 いまこの時の輝きを

序列，每次查询一个区间乘积的约数个数，膜$19260817$，值域$10^9$。

先爆力Pollard-rho分解一遍!

每个数只能有$O(\log v)$个质因子，可以爆力莫队，复杂度$O(n\sqrt{n}\log v)$。

每个数只能有$O(\log v/\log\log v)$个不同质因子，复杂度$O(n\sqrt{n}\log v/\log\log v)$。

刮痧不动了。考虑对质因子大小根号分治，我们取$v^\frac{1}{3}=1000$作为阀值，小的据说只有$168$个可以打前缀和，大的不超过两个可以莫队维护。这样就做完了。

总复杂度算一算，应该是$O(n(\sqrt{n}+v\frac{1}{3}/\log\log v)$，这里认为PR复杂度是$O(v^\frac{1}{4})$。

Ynoi2009 ra1rmdq

给一棵树，非负边权，还有一个结点序列。支持区间跳父亲，查询区间最大深度，深度是边权意义下的。

收录于洛谷省选计划。

Ynoi2011 D2T2

给一个序列，每次给出区间和一个$b$，查询最大的$x$，使得存在一个$a$，使得$a,a+b,...,a+(x-1)b$这$x$个数全在区间里出现过。值域$10^5$。

半平面数点

k-dt

最广为人知的是k-dt，但是它是假的，但是它随机数据是真的。

旋转扫描线

这个东西是说，考虑$n$条直线把平面分成$O(n^2)$个区域，我们爆力处理每个点在哪个区域，然后按照极角序转转转处理每个查询。复杂度是$O(q^2+n\log n)$。

分块

发现旋转扫描线复杂度不平衡，可以对查询分块处理，可以得到根号$\log$做法。

四分树/六分树

半平面数点的两个简单结构。

四分树每次选取两条直线，把平面分成四个区域，四个区域点数相同，那么每个半平面只可能递归到其中三个，所以复杂度是$T(n)=3T(\frac{n}{4})+O(n)$。解出来大概是$n^{1.8}$。

六分树每次选取三条直线(交于同一点)，把平面分成六个区域，六个区域点数相同，那么每个半平面只可能递归到其中四个，所以复杂度是$T(n)=4T(\frac{n}{6})+O(n)$。解出来大概是$n^{1.7}$。

当然可以继续搞下去，但是更高的划分数就会带来巨大的常数，算法竞赛中没什么意义。

结合旋转扫描线爆力，可以获得比根号略低的半平面数点做法。啊你说怎么结合?你就分治到一定大小改为爆力就好了，这可以做到$O(n^{1.442}\log n)$(四分树)之类的，没有找到六分树的分析。

Ynoi2019 宝石之国/CTS2021 半平面修改查询

CTS唯一一个没有被切的题/jy

平面上有一些点，每一个都有权值$a_i$，注意权值是抽象数据类型。每次操作求一个半平面的和，然后把半平面乘上一个抽象数据类型。$n\leq 2\times 10^5,q\leq 10^4$，基本运算次数不超过$2.5\times 10^7$。

考虑一个爆力。我们都知道$n$条直线把平面分成$O(n^2)$个区域，所以可以考虑这样的分治 :

一开始给每个点找到它所在的区域，接下来在时间上进行分治，每次递归下去的时候合并一些区域，回溯会把一些区域再分开。递归到底层的时候，只剩下两个区域，此时可以爆力查值，然后打一个修改标记。回溯的时候会切开一些区域，此时需要下传这个标记。这样分治复杂度是$T(m)=2T(\frac{m}{2})+O(m^2)$，解出来当然是$T(m)=O(m^2)$，当然除此之外还有一开始找区域的复杂度。

然后就可以考虑分块平衡复杂度，每$\Theta(\sqrt{n})$个操作一块，运算次数一共是$O(m\sqrt{n})$，他们分析了常数是$2\sqrt{6}$，看起来不是很大。

啊怎么找区域?这是平面图点定位。求出所有交点，扫描线扫过去，用平衡树维护一下就好了。所以你的时间复杂度其实是$O(m\sqrt{n}\log n)$/jy，lxl说有神秘数据结构可以砍这个$\log$，并且std也不是平衡树而是另一种神秘数据结构，常数似乎吊打平衡树。不过std不是lxl写的，我并不知道是什么。

Ynoi2019 美好的每一天~不连续的存在

树，点有颜色，还有一个序列$a$。每次查询一个编号区间，它在树上形成了若干连通块，每个连通块如果有$k$个出现奇数次的颜色，会对答案造成$a_k$的贡献，总答案是贡献和。

十一分块，势能均摊莫队。看下去之前我要提醒你，势能均摊莫队和我们说的势能法摊还分析没有关系。

考虑莫队。发现插入的时候，好像只能启发式合并/yun

启发式合并有什么问题?不能删除，横跳的指针复杂度也不是很对，因为一个块里面可能有巨量的操作，是可以构造出来的。

不管怎么说先回滚一个。每个块处理右端点在块里的询问，那么左端点的移动显然正确，右端点的横跳怎么保证?

考虑按照启发式合并中的实际代价，也就是操作的次数分块。如果设$f(l,r)$表示往$[l,r-1]$插入$r$的代价，注意到一件事 : $f(l,r)\leq f(1,r)$。这是因为树的性质，只有$r$这个点可以合并它周围的连通块，所以不插入它的话，区间越长，它周围的连通块不会变少。

所以你发现，不管左端点在哪，横跳的时候插入并撤销一整个块的代价，不会超过固定左端点在$1$时的代价。而$f(1,i)$之和是$O(n\log n)$，于是我们按照$f(1,i)$之和每$\Theta(\sqrt{n}\log n)$个分一块，就得到了一个$O(n\sqrt{n}\log n)$的做法。

这里如果有一个$f(1,i)$特别巨大，直接超过了你的阀值，我们就直接把它单独一块。这样的事情最多出现$O(\sqrt{n})$次，所以这里的复杂度没有问题。

注意我们在做这个的时候，只用到了$f(l,r)\leq f(1,r)$的性质，所以势能均摊莫队对这一类问题具有普适性，虽然这一类问题本来就没多少。比如如果把这题放到图上，这个性质就不存在了，因为多插入的点可能已经把一些连通块合并掉了。

Day4

模拟赛

怎么临时换人啊（

有一堆袋鼠，每个袋鼠有一个口袋。袋鼠有大小$a_i$和口袋大小$b_i$，保证$b_i<a_i$。你每次可以选择一个袋鼠$i$，把它放进另一个袋鼠$j$的口袋里，这要求$a_i<b_j$。每个口袋只能放最多一个袋鼠。求有多少种不能继续操作的情况，两个情况不同当且仅当存在一只袋鼠所在的口袋不同。$n\leq 300$。

容易想到把袋鼠画成线段，扔到数轴上。问题变成给线段分组，每组内部不能相交，并且不能存在一组结束在另一组开始之前。

把所有端点从小到大排序。如果我们扫到一个左端点，可以决策它是加入前面某一组，或者是让它单着。扫到一个右端点，我们可以选择把它留下来接到后面，或者让它单着。

设$dp(i,j,k)$表示考虑前$i$个，有$j$个需要单着的右端点，$k$个需要接上的右端点。那么决策是

当我们遇到一个左端点

干掉一个需要接上的右端点
如果没有需要单着的右端点，让这个左端点单着

当我们遇到一个右端点

让它留个接头
让它单着

转移即可，复杂度$O(n^3)$。

注意到需要单着的右端点，对转移的影响只限于有/没有，而不是是多少。改为$0/1$就是$O(n^2)$。

给$n,m$，求$(0,0)$走到$(n,m)$的单增下凸函数，最多经过多少格点。$n,m\leq 3000$。

考虑预处理所有可能的斜率(当然必须是既约的)，然后跑dp，从小到大枚举斜率依次更新，复杂度$O(n^4)$。

打表发现答案很小并且有单调性，可以证明只有$O(n^\frac{2}{3})$，所以进行维度交换，改设$dp(i,j,k)$表示考虑前$i$种斜率，走到$x=j$，用了$k$条线段，$y$至少是多少。复杂度变成了$O(n^\frac{11}{3})$。还是很慢!

有一个非常强力的剪枝，说的是如果我们选了一个线段，必须选横纵长度都小于等于它的所有线段，不然一定不优。这个听起来好像很对!

你发现这样剪枝之后，可用线段数量骤减，可以被证明是$O(n^\frac{2}{3})$的(，而原来是$O(n^2)$)。这样复杂度就是，$O(n^\frac{7}{3})$了!

啊你说怎么证这个数量?有一个结论是选两个数互质的概率趋近于$\frac{6}{\pi^2}=O(1)$，所以这个是否互质不影响渐进表现。然后一个线段左下方所有线段横纵长度和也很好算，然后就证完了（

Ynoi2010 Worst Case Top Tree/CodePlus #7 六元环

给一个序列，每个位置往左右第一个比它大的位置连边，支持单点加正数，数六元环个数。$n,m\leq 10^5$。

先不管修改。

建立大根笛卡尔树，于是除了树边，每个点还会向它左儿子右链和右儿子左链连边，这是经典结论?

注意到只要你画的够好，这就是一张平面图，我们连的边看起来是一种三角剖分。

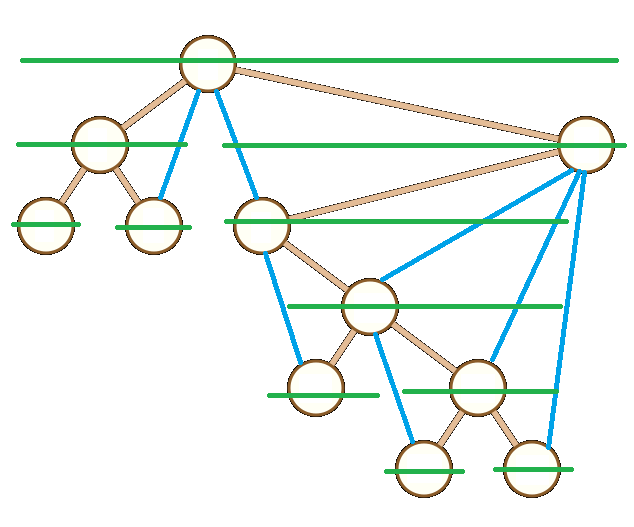
a tree

注意到如果我们选择了四个连通的点，一定存在唯一的方案选择上面两个点构成一个六元环，证明它需要大力分类讨论，不过这似乎是经典结论(如果三角剖分平面图的对偶图是树，那么它上面$k$元环与$k-2$个相邻三角形一一对应)。注意如果选到了根，那就不存在这样的方案了，所以需要一点特判。

四个连通的点……我们可以预处理所有四个点的树的可能形态，然后对于每个点维护下面选三个点的方案数，这个信息很好合并，于是问题变成动态笛卡尔树。注意到只加正数，说不定有什么性质。

注意到类似于Treap，大根笛卡尔树上加正数是可以用旋转描述的。试一试你发现转的过程中会把路径上的链转直，并增加$O(1)$个拐点，于是考虑利用拐点的均摊。类似于LCT，可以分析出一个$O((n+q)\log n)$的上界。

于是用LCT维护树，每次Access后在Splay上二分出所有的拐点爆力更新信息，就可以做到俩$\log$了。

另一种做法是，使用直链剖分，这是一种专用于维护动态笛卡尔树的结构。我们用类似LCT的方法维护每一条极长直链，直链就是边方向相同的链，此时类似于LCT的复杂度分析，可以得到优秀的一个$\log$复杂度。啊别问我怎么证复杂度，我只是课件的搬运工/cy

讲课

杜老师和毒老师/jy

Tube Master III

给一个$n\times m$的棋盘，每个格子有数，你要沿着格子边缘画若干闭合回路，使得每个格子四边中被回路经过的数量恰好是它上面的数。保证$n,m$中有一个是偶数。

Fillomino

$n\times m$的generals棋盘上有三个首都$A,B,C$，你要让三个国家分别占领$c_1,c_2,c_3$个格子，其中$c_1+c_2+c_3=nm$，并且每个国家都是连通的。构造方案，或者报告无解。$n,m\leq 500$。

科技 : bipolar orientation 双极定向。给一个点双连通图和两个点$s,t$，把图定向成一个DAG，并且$s$是唯一没有入度的点，$t$是唯一没有出度的点。做法请见三轮省集（

另一个科技 : 给定DAG和随便一个大小，可以把DAG分成这么大小的两部分，其中只有一边向另一边有边。

我们找到最小的点，然后从这个点开始模拟倒水，当然要给剩下两个点上方留空气柱。剩下的图性质看起来很好，可以用上面的科技搞定。

说实话我完全不理解为什么不能直接硬倒水。好像小的特殊情况比较恶心?

最大流

给一个DAG，每条边容量都是$1$，分别求以$1$为源点，$2,...,n$为汇点的最大流。$n\leq 10^5,m\leq 2\times 10^5$，$1$的度数$d$不超过$10$。

给$1$的出边一组不同的$d$维基向量，每个点的出边赋予入边的随机线性组合，那么答案就是入边的秩。

好像很有道理。怎么随?可以先对入边建线性基。复杂度$O(md^2)$。

Product

给一个随机质数$p$，然后$100$组询问，每次查一个随机数$a$，求一组$x$使得$x$们乘起来膜$p$是$a$，你的$x$的和不能超过$2500$。$p,a\leq 10^{18}$。

可以在sdfzoj contest1 C看到，题意是构造一个有向图使得$1$为根的内向生成树个数膜1e18+3恰好是给定的数，100组多测。由于sdfzoj的穿透不一定开不开，所以不挂link了。放一下我的题解。

考虑我们能完全操纵的边有哪些，你发现只有连到 $1$ 的边。大胆猜测用这些边就可以完成构造。
考虑如果只有连到 $1$ 的边，那么最后生成树个数是这些边重数乘起来。
注意到这里有一个取膜，这让我们想起sdptt2021 r2d4的时候dls讲的一个题叫product，做法是，考虑如果我们从 $2$ 到 $1$ 连了 $a$ 条边，那么问题变成凑出 $\frac{k}{a}$ 的生成树个数，由于膜素数这个数必然存在，并且它是比较随机的。随机一个比较小的数连上去，然后判断剩下的部分能否分解成比较小的范围(我取的是2.5e4)内的素数，如果可以那就找到了解，否则我们继续随一个比较小的数连上去，如果要连满了就重新开始。复杂度玄学，但是调参之后ct测出来1.1s。
然后就是一个绝妙的优化。瓶颈就在判断这个数能否分解成比较小的范围内的素数，我们可以在分解之前估计一下这个数是否有希望，如果不是很有希望我们可以直接return false。我的做法是，如果这个数不能被 $30$ 整除，那么它不是很有希望。然后就快了一倍，直接冲过去了。昨天为了这个优化我兴奋了一晚上（
测试了比较小的高合成数，取 $360$ 是最快的。

但是这个其实比较拉。我们可以把check分成若干段，每一段结束控制一下大小，如果大小过大那就认为没有希望了。对于较小的数可以直接筛出分解。

乘法逆元

给一个$p$，求$\mathrm{inv}(i)$的所有前缀最小值。

逆元看起来很随机，所以可以认为这个最小值个数是$\log$的。

然后你发现$i$这里前缀最小值大概是$\frac{p}{i}$级别。

Fast as Ryser

收录于集合幂级数。

Data Structure Quiz

$n\times n$的平面，先进行$q_1$次矩形加，再进行$q_2$次矩形求$\max$。$n,q_1\leq 5\times 10^4,q_2\leq 5\times 10^5$。

考虑矩形$\max$很不好。我们把它拆成前后缀然后合并就很好。但是怎么拆?

使用二区间合并结构，或者你可能知道猫树。对横轴进行分治，那么每个矩形会变成两个3-side矩形 : 一个区间的前缀拼上另一个区间的后缀。

考虑直接把查询定位出来，修改爆力处理影响，扫描线扫这个东西，要支持区间加/区间历史最大值，这很简单。

但是注意到一个修改矩形可能覆盖了很大的一片区域，所以我们复杂度就错了。优化也很简单，我们把每层的前缀询问放到一起处理，后缀另外放到一起处理，然后就变成要清空历史最值，这个也好做。复杂度$O(n\log^2 n+q_2\log n)$，认为$n,q_1$同阶。

Day5

模拟赛

有一排宝石，每个有颜色和正的价值，支持单点修改，查询给出$p,k$，问从$p$开始往右走，可以对于每块宝石选择拿或者不拿，最多不拿$k$块，不能拿同色的，拿到宝石的最大价值和，拿和不拿都不行的时候就停下。$n,m\leq 2\times 10^5,k\leq 10$。

简单题。考虑一个贪心策略，先能拿就拿求出最远走到哪，然后爆力在所有同色的中取一个最大值。

走到哪怎么维护?考虑维护颜色上一次出现位置$pre$，$i$不能拿相当于$pre_i\geq p$。$k$很小，所以我们爆力二分$k$次即可。

最大值开一堆动态开点线段树就好了，复杂度$O(nk\log n)$。

啊我数据结构学傻了。不用动态开点线段树，发现出现重复的最多有$2k$个元素，爆力找最大值即可。

给一个串$s$和一堆长度都是$m$的串$t_i$，对于$s$的每个前缀，以它开始玩硬币游戏。$n\leq 100,nm,\vert s\vert\leq 10000$。

建立ACAM，然后直接爆力高消，复杂度$O(n^3m^3)$。

可以乱搞!注意到矩阵很稀疏，进行random_shuffle，然后用带剪枝的高消硬跑。

正经做法还是很正常的。注意到Trie的叶子很少，所以分叉结点也很少，而ACAM上的所有转移要么是跳到儿子，要么是往上跳。

考虑主元法，假设已经表示出了所有比$u$浅的点和$u$的所有兄弟，那么当然可以表示出$u$。我们先设出根，然后给每个点，如果有$t$个儿子，把$t-1$个儿子设出来，剩下一个儿子算出来。总分叉数是$n-1$，所以就做完了。

也有PGF做法，不过那太恶心了。你想想把ACAM上主元法的过程自己手算是什么概念?

给一个大二进制数$x$，玩一个经典游戏

如果是奇数，变成$3x+1$
否则，变成$\frac{1}{2}x$

，问多少次变成$1$。保证$x$随机，位数$\leq 3\times 10^5$，2s。

观察大样例发现答案很小，据说不超过$10n$。

显然压位爆算，可以获得50pts。

考虑操作只取决于最低一位，我们可以考虑把最后若干位拿出来先搞出来接下来若干步要做什么操作，然后算出变换一口气做完，这样常数变得极小，可以获得100pts。

据说有一个真做法，不过被这样的爆力干爆了。

讲课

Evil Subsequence

给一个序列$a$和长度最多是$5$的序列$b$，求$a$有多少子序列和$b$的等价关系同构，也就是说如果我们取出子序列$a^\prime$，对于$i,j$有$a^\prime_i=a^\prime_j\Leftrightarrow b_i=b_j$。$n\leq 3000$。

你一看就知道这题随便做，不过场上最长的代码写了15k/jy

考虑对于$b$中出现超过一次的元素数量分类讨论。

没有，直接做就好了。
有两个，那么枚举它们两个分别对应什么，找到所有对应数出现的位置进行dp，剩下一个可以直接随便算。这样做的复杂度是线性的，总共可以得到一个$O(n^2)$的上界。
有一个，那么枚举它对应什么，不管剩下的直接算，然后容斥掉别的也有相同的情况，这个就是上一个东西。

Heavy Stones

给一排石子堆，你从一堆开始，每次选择这一堆左边或者右边相邻的合并过来，合并代价是两堆石子的大小之和。求从每一堆开始的最小代价。$n\leq 2\times 10^5$。

考虑只从一堆开始怎么做。

调整法。假设我们有一个方案，其中有一步放了左边一段，然后放了右边一段，那么什么情况下把它们换过来更优?

设前面放的总和是$w$，放的序列分别是$l_1,...,l_p$和$r_1,..,r_q$，总和分别是$sl,sr$，那么先左再右的贡献是$l_1+w+l_2+l_1+w+l_3+l_2+l_1+w+...+r_1+sl+w+r_2+sl+w+...$，先右再左类似。

你发现不同在于，先左再右我们加了$q$次$sl$，先右再左加了$p$次$sr$。所以先左在右更优当且仅当$q\cdot sl<p\cdot sr$，除一下就得到$\frac{sl}{p}<\frac{sr}{q}$，也就是说我们就是要比两段的平均值。

看到平均值就想到凸壳，相当于我们要维护左右两个$(i,a_i)$的下凸壳，然后把它们做类似于闵和的拼接。增量凸壳很容易，但是减怎么做?

其实很简单，我们只要倒着做一遍增量，然后撤销回去即可。可以用平衡树维护所有的凸壳上的线段，或者离线离散化用线段树来做。就做完了。

XX Open Cup, GP of Zhejiang B. Bitset Master

很多年以后来补，不知道是不是这天讲的了，并且是自己胡的不知道对不对（

有一棵树，每个点有一个集合，一开始每个集合只包含这个点自己，每次把一条边两端点的集合变成这两个集合的并，或者查询一个点出现在多少集合中。$n\leq 2\times 10^5,m\leq 6\times 10^5$，6s。

考虑$v$的集合包含$u$，当且仅当存在一个操作序列，使得它们连起来构成了路径$u\rightarrow v$，并且操作时间是递增的。

考虑如果静态怎么做，也就是说若干操作之后查每个点的出现次数。考虑点分治，我们处理分治块中每个点最早在什么时候走到分治中心，然后倒着处理每个时刻进入分治中心的点会跑到多少集合去，当然还需要每个子树跑一遍减去自己到自己的。这就做完了。

呃怎么处理每个点最早在什么时候走到分治中心?自底向上合并，用双指针扫父边和儿子们的父边即可，这个是线性的。

如果动态的话，显然这个点分治不能动态化，于是在外层套时间分治也是不可能的。考虑怎么直接魔改这个点分治。

考虑我们对于每次查询加一个走到分治中心的时间限制，如果超了那就扔掉。然后这个限制当然要继续约束从分治中心往各子树走的部分，这个怎么办?

需要详细考虑我们之前是怎么处理分治中心出发往各子树走的。你发现这个过程讲道理非常简单，就是从分治中心出发dfs，找到到达每个点的第一个时间，然后把所有时间拿下来离线基排。动态查询只需要加一个把查询时间在点分治上归并，跟这个一起双指针就行了。总复杂度$O(n\log n)$。

XX Open Cup, GP of Zhejiang L. LCM Sum

真**的毒瘤。感谢唐队长热心讲解/se

给$n,k$，求

\[\sum_{x=1}^n\mathrm{lcm}(x,x+1,...,x+k)\]

，$n\leq 10^{18},k\leq 30$，膜$10^9+7$，7s。

考虑我们怎么算$\mathrm{lcm}$，就是每个质因子取最大次数乘起来嘛。

你发现一个事情，这个最大次数性质一般，但是不是最大次数的性质很好 : 考虑$k$以内$p$的最大幂$p^e$，如果两个$x_1,x_2$膜$p^e$相同，那么$x_1^\overline{k+1}$和$x_2^\overline{k+1}$里面不是最大次数的次数和相同。

于是想到把$\mathrm{lcm}(x,x+1,...,x+k)$表示成$\frac{1}{c}x^\overline{k+1}$，对于膜$L=\mathrm{lcm}(1,...,k)$相同的$x$，得到的$c$也相同。

打个表发现$L$只有1e12级别，所以我们已经砍掉了1e6（

啊具体怎么算?直接对于$L$以内每个数质因数分解，然后暴力计算每个余数$r$对应的$c$，然后随便计算每个$r$是多少$x$膜$L$的余数($r\leq n\bmod{L}$就是$\lceil\frac{n}{L}\rceil$，$>n\bmod{L}$就是$\lfloor\frac{n}{L}\rfloor$)

然后这个1e12就很像要开根号的样子，我们尝试折半。把$30$以内的十个质数差不多平均地分成两份，分别记为$L_1,L_2$，两个数都是$\Theta(\sqrt{L})$ 级别。那么如果知道$r$膜$L_1,L_2$的值$r_1,r_2$，根据CRT我们知道$r$等于$c_1r_1+c_2r_2\bmod{L}$，其中$c_1,c_2$是两个只跟$L_1,L_2$有关的常数。

这就非常好!下一步就是上面的式子太难算了，我们需要拆贡献。

那个$\frac{1}{c}$很好搞，因为它是每个质因子独立的，贡献方式就是简单的相乘，我们只需要分别膜$L_1,L_2$算一遍(这是$O(\sqrt{L}\log L)$)，之后合并的时候很容易搞定它，所以先把它去掉好了。

这个上升幂在这里单着，考虑使用组合数，和范德蒙德卷积!

\[\begin{aligned} &\sum_{x\bmod{L}=r}x^\overline{k+1}\\ =&\sum_{i}(iL+r)^\overline{k+1}\\ =&\sum_{i}(iL+r+k)^\underline{k+1}\\ =&(k+1)!\sum_{i}\binom{iL+r+k}{k+1}\\ =&(k+1)!\sum_{i}\sum_{j}\binom{iL+k}{j}\binom{r}{k+1-j}\\ =&(k+1)!\sum_{i}\sum_{j}\binom{iL+k}{j}\binom{c_1r_1+c_2r_2}{k+1-j}\\ =&(k+1)!\sum_{i}\sum_{j}\binom{iL+k}{j}\sum_{t}\binom{c_1r_1}{t}\binom{c_2r_2}{k+1-j-t} \end{aligned}\]

然后就可以分别算三个序列然后卷卷卷了。

后两个直接爆算就行了，问题在于怎么算第一个。注意到这是关于$i$的$j$次多项式，可以硬插出来，所以就可以算巨大的数了。这里为了保证复杂度不多$k$需要使用线性的拉插。

现在还有两个问题 : $i$的上界，也就是膜$L$得$r$的$x$个数不固定；上面我们认为$r=c_1r-1+c_2r_2$，但是实际上可能需要减一个$L$。

不过你发现，如果我们固定了一个$c_1r_1$，那么第一个问题把$c_2r_2$分成了两种，其中拼起来得到$r\leq n\bmod{L}$的$c_2r_2$的值是一个区间；第二个问题把$c_2r_2$分成了两种，其中需要减$L$的是一个后缀。于是先排个序，可以用三个双指针维护三个分界点，它们把$c_2r_2$分成了四段，每一段内部的合并都是一样的，分类讨论一下就好了。

然后就是要支持求区间(那个序列的)和，可以用一个前缀和来解决。总复杂度是$O(\sqrt{L}(\log L+k^2))$，卡卡常就可以过了。

新年的邀请函

Link Cut Digraph

有向图，支持加边，然后输出强连通点对数量。$n\leq 10^5,m\leq 2.5\times 10^5$。

无向图可以直接并查集，所以考虑求出每条边在什么时刻进入一个SCC，也就是什么时候它的端点在同一个SCC。如果求出来这个就也可以并查集了。

整体二分。先加入左半边的边，判断查询边的答案，然后删掉这些边并递归左边，再加入左半边的边进行一轮缩点，最后递归右边。

不过发现一条边会被加一个时间后缀，这样它要是一直没被缩点那就死了。

考虑如果它在左区间没被缩点，我们把它扔下去也没啥影响，不如直接不扔。额外传一个有用边的集合就好了，此时每条边都只会递归到一边。复杂度$O(n\log n)$。

随机数

有一个随机数列$a$，把它打乱之后加$k$膜$m$得到数列$b$，给你$a,b$，求$k,m$。$n\geq 10^5,m\leq 10^{10},a_i\leq 10^{18}$。

注意到最大值应该很接近$m$(类似于骗分过样例未知模数点)，算一下你发现大概是1e5级别，可以考虑枚举。

注意到不管怎么打乱，总和是不变的，所以可以解方程$\sum a_i+nk\equiv\sum b_i\pmod{m}$。解可能不止一个，但是因为是随机，数量很少，据说是期望$O(1)$。

怎么判定一组$m,k$是否可行?考虑随机一个$a$，用哈希表找对应的$b$，当$m$很大的时候，错误的$k$得到正确对应关系的概率将会非常小，而$m$很小可以爆力。

一个优化是，考虑这个$+k$很恶心，打乱也很恶心，但是第一种在差分的意义下不变，第二种在枚举所有对求和的意义下不变，所以我们考虑$\sum_{i,j}(a_i-a_j)$和$\sum_{i,j}(b_i-b_j)$，它俩膜$m$是同余的。我们可以用$m$是否整除这俩东西的差来判一个$m$是否可行。

然而这还不够好，因为你发现拆开之后它不剩啥了/jy

可以平方一下!这样剩下的$m$将会非常少，爆力判就好了。

Mystery Square

给一个二进制完全平方数，但是有最多$40$个位置是?，你需要求出它实际上是什么。最多有$125$位。

考虑如果我们确定了前一半或者后一半，就几乎可以确定这个数，所以根据平均值不等式我们知道前后至少有一边?不超过$20$个，可以爆力枚举。

啊你说怎么确定?确定了后一半的话，可以写出一个$x^2\bmod{2^k}=x_0$这样的东西，如果你学过任意模数Cipolla，你应该知道只有一组解。确定了前一半的话，硬开两遍，得到的可能的解很少，好像是$O(1)$的。

XIV OpenCup, GP of Saratov, Problem I. Presents

有一个长$m$的等差数列$s+di$($i$从$0$开始)，现在把它膜$n$并打乱给你，保证数不重复，但是不保证它确实是等差数列。求一组$s,d$，或者报告它不是等差数列。$n\leq 10^9,m\leq 10^6$。

首先考虑，如果我们知道了两个在等差数列中相邻的数，就可以知道$d$，$s$自然也知道了。

考虑一个很奇妙的事情，我们随便在这里面选一个数$y$，那么满足$x+z\equiv 2y\bmod{n}$的$(x,z)$在原等差数列中看起来应该是关于$y$对称的。删掉$y$和所有这样的$(x,z)$，我们就删掉了一个前缀或者一个后缀，剩下的还是一个等差数列，然后就可以递归下去了。

啊可以画个图 :

deletion

然而取膜可能膜出奇奇怪怪的东西，我们可能删掉了一个不取膜情况下不应该删掉的位置。

但是注意到一件事情 : 如果我们删掉了一对东西，那么在原等差数列中，这一对里面的对和外面的对也会被删掉。画个图吧?

wrong deletion

比如这里我们删掉了红的，那么绿的和蓝的也会被删掉。所以这样的乱删一定会扩展到两边，也就是说删掉的是一个前缀一个后缀，留下的一定是一个区间，所以还是一个等差数列。

诶等等，这里的蓝色中间那个并不能跟别的东西配对啊!实际上这个好说，我们只要让它和自己配对就行了。

你发现如果我们随机一个中间的数，期望会删掉一半，所以删$\log$轮之后就会变成$O(1)$，我们就可以在剩的很少的时候爆力枚举一个$d$了。复杂度是$O(m\log m)$。

Collections in Containers

有$n$个$d$维向量$v_i$，满足如果一个向量存在，所有各维都$\leq$它的向量也都在。

给一个向量$c$，要求一个排列$p$，使得所有$v_i+v_{p_i}$的各维都不超过$c$。$nd\leq 10^5$。

Tube Master II

或者叫Loopy?

说的就是有一个棋盘，有的格子里有数，你要画一条闭合回路，使得它经过每个格子边缘的次数，等于格子里的数。

这道题有一些不同，说的是你可以画若干闭合回路，并且必须一直拐弯，并且每个格子都有数。

做法很简单，直接从上到下模拟就行了，因为玩一玩你会发现如果确定了一个格子上面的情况，那么这个格子要么有唯一解，要么无解。

Day6

模拟赛

T1 city

给一张无向图，一开始速度都是$1$，你可以花一块钱把一条边的速度增加$1$，一条边的通过时间是$1$除以速度。现在有两个人分别从$s_1,s_2$出发前往$t_1,t_2$，求一种方案使得他们到达目的地的总时间最小。$n,m\leq 5000$。

考虑用两条最短路的经典trick，我们枚举中间相交的一段，然后就得到一些边经过一次，一些边经过两次，可以用三分求出最优分配方案。

但是带$\log$过不去，不过我们只要发现一种长度相同的情况下，另一种长度越短越好，所以我们直接筛一遍去掉一定不优的，就只需要$O(n)$次三分了。

T2 button

有一个五位十进制显示器，你要用它玩一个猜数游戏，每次操作可以改一个数位，或者查询现在显示的数是大了，小了还是对了。$100$询问，每次给要猜的数的区间$[l,r]$，问如果采用最优方案，最坏情况下需要多少次操作。$l,r\leq 99999$，3s。

容易想到一个区间dp，我们设$dp(i,j,0/1/2)$表示区间$[i,j]$，显示器上现在是$i-1/j+1/0$的答案，复杂度$O(n^3)$。

区间dp状态是$n^2$的，没有前途。考虑答案很小，最大不超过$45$(实际上是$42$)，并且固定一个端点的话具有单调性，可以考虑维度交换。设$l(i,j)$表示显示屏上的是$i$，从$i$出发往左，最多进行$j$次操作，可以猜到哪里，$r$则是往右。

比如如果我们要求$r(i,j)$的话，当然考虑第一次猜什么。如果从$i$变成它需要$d$次操作，那么猜它还需要一次操作，剩下$j-d-1$次。所以它需要可以在$j-d-1$次操作内一直猜到$i+1$，此时可以让它尽可能往右走来更新答案。也即如果$k$满足$l(k,j-d-1)\leq i+1$，那么我们可以用$r(k,j-d-1)$更新$r(i,j)$。

这个转移性质还是很差……

不过位数只有$5$，可以考虑做一些奇怪的事情。

折半。两个数用$d$次可以互相转化，当且仅当存在一种方案把两个数中的分别$d$个位置换成?，从而使得两个数完全相同，于是我们可以利用这个进行双向的转移。

如果没有$l(k,j-d-1)\leq i+1$的限制，我们可以对于每个已经算完的状态，枚举所有把一些位换成?的方案，然后压成十一进制数，开一排桶，把$r$扔进状态对应的桶，每个桶取$\max$。转移的时候还是枚举所有换成?的方案去桶里查就好了，每个数的枚举量降低到$2^5=32$。

有这个限制也很简单，排个序扫描线就好了。复杂度无法计算!反正能过（

T3 cake

原题 ICPC2020 Shanghai J Octasection，收录于一轮省集。

讲课

subset

给一个序列，求两个和相同的不交非空子集。$n,a_i\leq 10^5$。

经典题。考虑前$22$个数即可，因为$2^{22}-1>22\times 10^5$，根据鸽子原理一定有解。

中位数

有一个序列，每一时刻，每个数会变成上一时刻相邻两个数和它的中位数，左右两边始终不变。求多少轮之后序列变得稳定。

看到中位数，考虑转成$01$序列。我们枚举每个数，把$\leq$它的搞成$0$，$>$的搞成$1$。

发现一个$0$连续段和$1$连续段都是不变的，只有$01$交替的段会每一时刻左右各缩短$1$，set维护最长的交替段即可。

啊这为什么是正确的?我们实际上是在枚举最后一个稳定的位置是什么数。

有一个神仙线性做法，看懂了来补。

最短路

点带权的图，求$s$先走到$m$再走到$t$的最短路，一个点被经过多次只算一次。$n,m\leq 300$。

无向图的话只可能有一段交，所以就很好做。但是有向图不行。

考虑一个dp，设$dp(i,j)$表示从$i$走到$m$再走到$j$的最短路，但是它没法考虑重复的问题。具体一点，你发现它可以解决两个点向同一方向走过去的重复，但是不能解决这种不同方向的 :

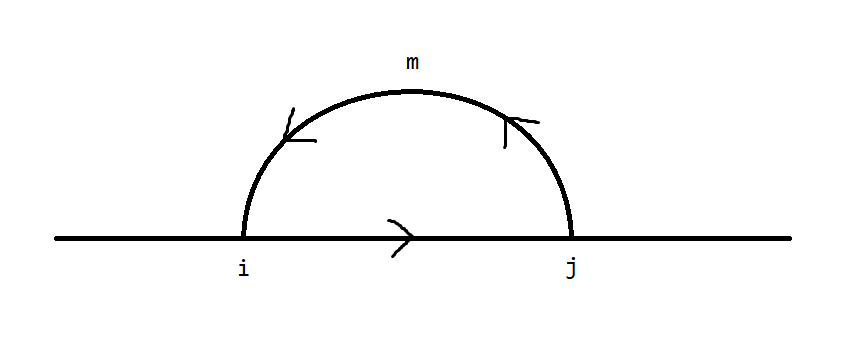
a path

啊这个不同方向可能有点表述不清，它的含义是两个点分别在向$m$走的时候和离开$m$之后经过这一段路。

如果我们要重复走中间这一段，需要让$i$走到$j$，让$j$经过$m$走到$i$，这会加上$dis(i,j)$的代价。然后剩下的部分，可以把状态改成$dp(j,i)$，也就是让$j$走到$m$再走到$i$，你发现$i\rightarrow j$这一段恰好变成了经过两次!草草草草草草草草，这也行?

转移可以用Dij解决，复杂度$O(n^3\log n)$。

01背包

每个物品有权值$a_i$，要求权值和$\leq c$且最大，输出最大值。$n,a_i\leq 2\times 10^4,c\leq 10^9$。

先贪一下得到一个很大的答案 $t$，那么 $c-t<v$。于是把选过的取负，问题变成 $\leq c-t$ 的最大的解，这就非常好对吧。

我们希望把过程中所有数的值都控制在 $O(v)$ 范围内。一个想法是轮流取正数和负数，这个想法看起来非常对对吧，但是直接做是 $O(n^2v)$ 的。

维度交换，设 $dp(i,k)$ 表示考虑前 $i$ 个正数，要凑出 $k$，至少要取到第几个负数，正确性，因为我们是依次考虑，显然取的越少转移越自由，这样状态数是对的了。转移考虑选不选下一个正数，或者枚举下一个选的负数，还是 $O(n^2v)$ 啊。

这里显然有单调性 $dp(i,k)\leq dp(i-1,k)$。注意到 $dp(i-1,k)$ 已经做过的转移 $dp(i,k)$ 不需要再做，也就是说下一个选的负数只需要在 $[dp(i,k),dp(i-1,k))$ 中枚举，这样复杂度就是 $O(n(n+v))$ 了。

数

定义$f(x)$为$x$加上$x$的各数位最大值，单次询问从一个$x$开始迭代$k$轮之后会得到什么。迭代一轮指的是$x:=f(x)$。$x,k\leq 10^{18}$。

仔细想想发现直接模拟没啥可优化的。

考虑按位确定答案。你发现这里有个单调性，就是越加越大；另一个性质是每次加的一定是$1,...,9$中的一个。

这告诉我们什么呢?如果我们已经确定了答案前面的位，这一位至少是$t$，当且仅当这一位填上$t$，后面全都填上$0$，需要的操作次数少于$k$。当然每一位处理完需要把$k$减去我们用掉的。

呃等等，最后一位可能并不是$0$，不过只需要在$0,...,9$中再枚举就行了。位数少的可怜，不需要考虑复杂度（

定义一个数是标准的，当且仅当它除了最高位和最低位全是$0$。

然后是枚举的一些细节。我们需要先把这个数加成标准的，这样每次我们枚举到的这一位增加$1$，都只需要计算一个标准的后缀进位一次需要的操作次数。

怎么把一个数加成标准的?呃可以从最低位开始往前做，这样处理到$i$位时，前$i$位已经是标准的了，每次要做的事情都是让一个标准的后缀进一位，这跟前面说的剩下的部分所需要的信息是一样的。如果操作次数并不足以把整个数加成标准的，那就直接结束就好了。

现在问题是，我们需要计算一个标准的后缀进一位需要的操作次数。具体一点，计算$f(i,j,k)$表示后$i$位，其中除了最后一位是$j$，别的位全是$0$；此外前面的最大值是$k$；至少要多少步才能向$i+1$位进位一次。当然，还需要设$g(i,j,k)$表示这次进位之后最后一位是什么。

这个东西可以数位dp搞定。考虑我们往$i$位进位十次，就会往$i+1$位进位一次了。

Mr. Panda and Typewriter

有一个打字机，支持在最后加一个字符，copy已经打过的一个子串，paste到最后，分别有不同的代价，剪贴板只能存一个串，求最小代价来打出$s$。$n\leq 5000$。

考虑dp。直接把剪贴板设进状态显然爆炸，我们考虑在打出这个需要的串的时候就copy下来，所以可以设$dp(i,j)$表示打了前$i$个，剪贴板里是此时后$j$个的最小代价。

转移有

直接填一个
copy之前的一段
paste到后面的第一个出现位置，中间爆力加字符

hash一下或者SAM硬上，就$O(n^2)$了。

Game on the Tree

收录于一轮省集(D4T3)。

Mr. Panda and SAD

有一排字符串，每个长度不超过$20$，总长不超过$2\times 10^6$。把它们接起来得到一个串，最大化里面的SAD子串个数。

SAD长度只有$3$\jy

考虑串只有这么几种 :

A
…S
…SA
AD…
D…
AD…S
AD…SA
D…S
D…SA
…

(几种)。

发现有一些拼接是一定的，比如S肯定和AD拼起来，SA肯定和D拼起来。

这个A看起来很不合群。我们枚举有多少A和…S拼起来，剩下的就和D…拼起来或者单着了，贪心地我们先拼起来。然后就显然贪心地拼了。具体地，我们

先拼…S+AD…这样的
再拼…S+AD…S这样的
最后乱拼

。最后是环的问题，一部分我们想拼的东西个数相同的时候需要特判减去$1$，比如D…S+AD…SA这样的。

Infimum of Paths

有一个边权都是$0,...,9$的有向图，定义一条路径的权值是它的字典序除以$10$的长度次方，比如路径边权依次是，$1,1,4,5,1,4$，它的权值就是$0.114514$。求$0$到$1$所有长度有限路径权值的最大下界，可以证明这个数是一个有理数，输出它膜$998244353$的值。$n\leq 2000,m\leq 4000$。

考虑为什么会是有理数。先以最小字典序走到一个环上，然后在环上转转转，在无限步之后走到$1$去，所以它确实是无限循环的。啊为什么不能在两个环上转转转?显然在其中某一个上转转转要优于另一个。

做一个类似bfs的东西，对每个点求出用每个步数走到它的最小字典序路径是从哪里来的。这个复杂度是$O(Tm)$，$T$是我们需要的最大步数。

注意到$n+1$步一定会走到一个环上，所以我们进行$n+1$步就足以找到所有无限循环的路径，其中每个点恰好对应了一条权值极小的路径，可以$O(n)$求出一条这样路径权值的循环节(也就是最后走的环)，然后用等比数列求和把它化成分数。这部分是$O(n^2)$。

剩下的都是没有成环的路径了，长度都不超过$n$，可以对于每个长度从$1$出发找回去，这部分还是$O(n^2)$。所以我们上面的bfs中只需要$n+1$步，复杂度是$O(nm)$。

还有一个小问题 : 要走环的话，前提是可以从环上走回去到$1$，所以需要先删去所有不能到$1$的点。

Non-Maximum Suppression

平面上有一些边长全是$S$的正方形，我们按照编号从小到大枚举正方形，每个正方形$A$会删掉满足$\frac{A\cap B}{A\cup B}\geq$一个常数$c$的正方形$B$。求哪些正方形活下来了。$n\leq 10^5,S\leq 10^7,0.3\leq c\leq 0.7$。

边长都相同就很好。用$S\times S$的正方形给平面划分区域，那么每个正方形只会覆盖四个相邻区域的一部分。对每个区域开一个vector，然后就可以每块分开搞了。

然后我们考虑一个正方形没有被删掉，

Game

Alice和Bob在玩军棋，但是规则有些不一样 :

两个人拿着两个完全的棋子序列(也就是说有所有$24$个棋子)，每次取出第一个来拼，谁打空了谁就输了。为了保证游戏可以结束，地雷和地雷也会对掉。

现在Bob有一个随机的棋子序列，你要帮Alice找到一个能赢Bob的棋子序列，并且随意交换其中两个棋子，Alice还是可以赢Bob。$100$组数据。

注意到Bob是随的，所以随一个有一半的概率可以赢，但是直接随出答案需要大约$24^2$次，check一次需要$24^3$，加上$100$组数据，难以接受。多测就是为了卡你这个（

随机爬山。估价函数是有多少种交换使得Alice还可以赢Bob。这样出答案的次数会大大减少，表现优秀。

Day7

模拟赛

T1 tree

有一棵白色的树，点有点权，现在你要把一些点涂成黑色，然后计算这棵树的代价 :

如果一对黑点是祖孙关系，并且祖先比后代点权小，代价增加$1$
如果一对白点是祖孙关系，并且祖先比后代点权大，代价增加$1$
如果一对白点不是祖孙关系，代价增加$1$
对于每个白点，代价增加它的深度

。对于涂黑$0,...,n$个点的方案，计算代价的最小值。$n\leq 5\times 10^5$。

发现白点对更多情况下是产生代价，同时我们确定黑点个数的情况下白点对总数也确定了，所以可以尝试把代价反过来。

如果一对白点，代价增加$1$
如果一对白点是祖孙关系，并且祖先不比后代点权大，代价减少$1$

这就很好!然后做这种题，我们当然猜测选$k$个点的方案一定包含选$k-1$个点的方案，所以可以维护每个点变黑的代价。

你发现这东西最后变成了 : 每次我们选一个点，就把子树中以及到根链上所有和它点权相同的点代价增加$1$。对每种颜色内部的标号离散化一下，然后树剖+BiT维护即可，复杂度$O(n\log^2 n)$。

据说有神秘$1\log$做法，可我不会/cy

T2 Travel

给一个有向图，满足每个SCC都是一个环，再给一个数$k$，求有多少有序路径对$(p_1,p_2)$，满足每个点都被两条路径总共经过至少一次且不超过$k$次。$n\leq 2000,m\leq 4000,k\leq 10^9$，膜$998244353$。

如果没有环并且没有$k$就很好做，我们可以直接拓扑排序，按照拓扑序重标号，然后进行dp。设$dp(i,j)$表示第一条路径走到$i$，第二条走到$j$，两条路径覆盖了$\max(i,j)$之前的所有点的方案数。

讲课

Travel

草，原来T2就在课件上/jy

Bytelandia States Union

Border Similarity Undertaking

给一个$n\times m$的小写字母组成的矩阵，问有多少长方形，使得边界上字母都是一样的。$n,m\leq 2000$。

分治。选取长的一边切开，然后预处理一些东西，在短边上$O(n^2)$爆力合并就好了。因为短边短，这样做不影响复杂度。复杂度是$O(nm\log nm)$。

GCD Land

有$n$个点，权值一开始是$1,...,n$。你要找一个$x$，使得给所有权值加上$x$之后，对不互质的点对连无向边，得到的是连通图。$n\leq 1000$，你的$x$不能超过$n$位(十进制)。

考虑如果我们要从$i$往$i+p$连边，我们可以写出一个方程$x+i\bmod{p}=0$，也就是$x\equiv -i\pmod{p}$。如果所有的$p$互质，我们就可以得到唯一解。

考虑让每个质数(的幂)只用一次。这样肯定有唯一解。

有这么一个神奇的数 : $\mathrm{lcm}(1,2,...,\frac{n}{2})$。如果我们让$\frac{n}{2}$最后的权值是这个数，那么就可以向所有数连边了!

呃不过看起来我们连不到$\frac{n}{2}\pm 1$。尝试修补一下。

发现可以这么搞 : 我们从那个$\mathrm{lcm}$中拿掉$\frac{n}{2}$以内最大的两个质数$p_1,p_2$，转而用它们来分别帮$\frac{n}{2}\pm 1$连边。具体地，$\frac{n}{2}-1$连到$\frac{n}{2}-1+p_1$，$\frac{n}{2}+1$连到$\frac{n}{2}+1-p_2$。

由于我们拿$p_1,p_2$做了一些奇怪的事情，原来用它们连起来的数现在也可能不行了。具体地，$\frac{n}{2}\pm p_1,\frac{n}{2}\pm p_2$是搞不到的。我们可以选取大于$\frac{n}{2}$的最小的四个质数，让它们也连一连。这样就有一堆同余方程，高精CRT即可。

在$n$很小的时候可能会出现质数不够用的情况，需要爆力。

Day9

模拟赛

人均250，垫底了/ll

T1 tree

有一棵树，你要任选一个点开始，每一步可以走到子树里的一个点，或者结束这个过程，求方案数。为了让题目更难一点，每个点有一个标记，还有另一棵树，要支持给所有具有某种标记的点挂上另一棵树中的一个子树，新挂的点的标记等于它在另一棵树中的编号，每次修改后再次输出答案。$n,m,q\leq 5\times 10^5$，其中$m$是另一棵树点数。

先倒过来转成每个点向根走，这样方案数就是$\sum 2^{dep}$，然后考虑对于每个标记分别维护，发现接上子树就是对子树里的编号做一个带系数乘，dfs序转成区间带系数乘，线段树维护即可。

给一个棋盘，有些位置是障碍。多次查询从一个点出发，只能往右或往下走，不能走障碍，能不能走到另一个点。$n,m\leq 500,q\leq 6\times 10^5$。

呃如果你做过旅行者，你就知道要分治。

直接爆力处理查询会被卡常，可以用Bitset预处理一下，复杂度变成$O(n^3\left(1+\farc{\log n}{w}\right)+q\log n)$，就卡不死了。

讲课

AGC036D Negative Cycle

没有负环等价于最短路存在，所以我们可以写出所有的松弛，然后

Day10

模拟赛

人均300，垫底了/ll

T1 mushroom

给一棵树，定义一个连通块的权值是编号$\gcd$的连通块大小次方，求所有连通块权值和。$n\leq 200000$，3s。

枚举$\gcd$，莫反一下，然后随便做即可。复杂度是，$\sum_{i=1}^n d^2(i)=O(n\log^2 n)$。

T2 samsara

T3 hole

有一个数轴，数轴上有一些球和洞，现在你可以把所有球统一左移一格或者右移一格，球碰到洞就会掉进去，问全都掉进去之后有多少种可能情况。$n,m\leq 10^5$。

考虑一个球只可能掉进左边或者右边第一个洞。

/kk/kk