5.19 决策单调性与四边形不等式
抽象
决策单调性优化的dp总是可以转化成在矩阵中求每一行最小值的问题。比如经典的方程
\[dp(i)=\min_{j<i}(dp(j)+w(i,j))\]就可以用$A_{i,j}=dp(j)+w(i,j)$构成一个矩阵$A$,这样$i$行的最小值就是$dp(i)$。以下默认一行的最小值是位置最大的最小值。
啊当然我们一般没有必要整个求出这个矩阵,它往往可以通过某种方法快速计算。
决策单调性优化的基础是,这个矩阵是单调矩阵。单调矩阵指的是每一行的最小值位置单调不降。
有些问题的性质更优美,它的矩阵是完全单调矩阵,也就是它的每个子矩阵都是单调矩阵,子矩阵说的是删去若干行列得到的矩阵。满足四边形不等式的都是完全单调矩阵。
能适用于单调矩阵的只有分治,而二分栈和SMAWK及其扩展都只适用于完全单调矩阵。
分治
北大集训2018 ZYB的游览计划
给一个排列和一棵树,把排列划分成$k$个区间的并,使得 每个区间并上$1$在树上的最小斯坦呐树边数 的和最大。$nk\leq 2\times 10^5$,注意是$nk$不是$n,k$。
发现这个转移用到的最小斯坦呐树边数有四边形不等式(反着的),于是是完全单调矩阵,可以考虑分治或者二分栈,SMAWK不会真有人在场上写吧。
分治的优秀性质就体现在这里。这个转移的权值不好直接计算,但是可以类似莫队移动指针,维护一个set,可以在$O(\log n)$内增删一个元素。直接移动的话发现复杂度就是$O(nk\log^2 n)$。
在完全单调矩阵中,定义一列是冗余的,当且仅当任何一行的最小值也不在它上面。
你发现有一个很好的性质,那就是对于两列$i,j$,
-
如果$j$列在$k$行比$i$列更差,那么在此之前它总是比$i$列更差,也就是$j$列在$k$行之前是冗余的。
-
如果$j$列在$k$行不比$i$列更差,那么在此之后它还是不比$i$列更差,也就是$i$列在$k$行之后是冗余的。
证明?否则把这两列拿出来就不是单调矩阵了,不满足完全单调矩阵的定义。
注意单调矩阵并没有这样的性质。
SMAWK及其扩展
SMAWK基于一个有趣的操作reduce。它可以在线性时间内把需要求解的完全单调矩阵砍掉一些冗余列,具体地,可以把$m\times n$变成$m\times\min(n,m)$。
reduce操作从左往右扫过每一列,维护一个$k$,表示只考虑前$k$列的话,它们在主对角线上方都是冗余的(不包含主对角线)。
比较$A_{k,k}$和$A_{k,k+1}$,如果$A_{k,k}\geq A_{k,k+1}$,那么第$k$列整个都没有用了(因为主对角线上方已经没用了),可以删掉第$k$列,并让$k:=k-1$(因为$k+1$列还不一定在主对角线上方冗余),注意这里删除之后主对角线也会实时更新。删除一列的操作,因为不用随机寻址列,可以用链表维护没有删除的列。
反过来,如果$A_{k,k}<A_{k,k+1}$,那么说明第$k+1$列在主对角线上方全部冗余了,让$k:=k+1$。呃如果此时$k=n$那就不好了,不过我们可以直接删掉$k+1$列。
复杂度显然是线性。
SMAWK的主过程,每次选出偶数行构成新矩阵,reduce删掉多余列然后递归下去求解,然后每个奇数行在相邻偶数行的决策点之间爆力枚举。除了递归,每一步显然都是线性的,如果$n,m$可以不同阶,最后可以分析出一个$O(m(1+\log\frac{n}{m})+n)=O(n+m)$的复杂度。
可惜SMAWK看起来有四倍常数,并且不能处理单调矩阵,也没有指针移动的性质,跟分治比起来没有很大优势。
Wilber和Eppstein
可以做到和二分栈一样的事情,只不过是线性的。
常数巨大并且难写,OI中目前只有理论价值,换句话说你口胡的时候可以认为自己砍掉了一个$\log$。
四边形不等式DAG定长最短路问题
Open Cup 18~19 GP of Zhejiang I. Post Office 5
邮局 上环。
$n,k\leq 2.5\times 10^5$,5s,构造方案。
定理 满足四边形不等式的DAG定长最短路的凸性
邮局 这个问题,观察dp方程,可以转化成DAG上定长最短路问题,同时这个边权是满足四边形不等式的。
呃具体怎么转化……就是如果$i<j$,那么$i\rightarrow j$的边权是$w(i,j)$,然后求从每个$i$到$i+n-1$,经过$k$条边的最短路,取$\min$就是答案。
设$f(k)$表示长$k$的最短路长度,考虑$f(k+1)-f(k)\geq f(k)-f(k-1)$这个东西(就是凸性),可以证一个更强的结论 : 对于$s<r<t$,有$f(s)+f(t)\geq f(r)+f(s+t-r)$,这个代入$s=k-1,r=k,t=k+1$就得到凸性。
考虑设$f(s)$的路径是$p_0\rightsquigarrow p_s$,$t$的当然是$q_0\rightsquigarrow q_t$。
我们设$v=r-s$,如果可以找到一个$i$使得$p_i\leq q_{i+v}<q_{i+v+1}\leq p_{i+1}$,那么构造$p_0,…,p_i,q_{i+v+1},…,q_t$作为$f(s+t-r)$的路径,$q_0,…,q_{i+v},p_i,…,p_s$作为$f(r)$,根据四边形不等式容易得到它不比调整之前差(这个也可以直观理解,就是调整之后一条变长一条变短,而四边形不等式也是一种凸性)。
呃这里可能不是很好理解,我们画个图来看看。这是$s=5,r=7,t=9,v=2$的一个可能情况,红色是$f(s)$,蓝色是$f(t)$,剩下的懂的都懂。
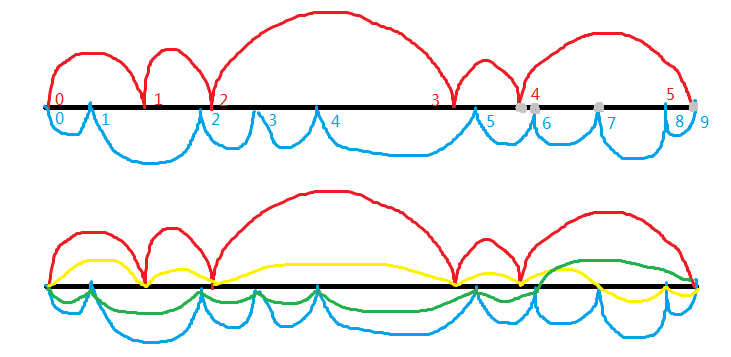
那么怎么说明一定可以找到这样的$i$?
你发现一开始$p_0=q_0$,最后$p_s=q_t$,而$s<t$,直观来看$p$的平均跨度应该比$q$要大。然后你发现$r$是任取的,所以看起来对于$[1,t-s-1]$中的所有$v$都应该可以找到这样的$i$。
诶你发现看着上面那个图就显得非常直观。如果不存在这样的$i$,那么最后显然就不满足$p_s=q_t$了,具体怎么说明,大家懂的都懂……嗯!
然后我们就可以wqs二分,爆力枚举起点搞就可以了。复杂度$O(n^2\log v)$。啊还有构造方案……最后再说!
路径单调性和路径不交性
容易证明,如果$u_1<u_2,v_1<v_2$,那么$u_1\rightsquigarrow v_1$和$u_2\rightsquigarrow v_2$的字典序最小的最短路一定不会相互穿过。证明方法就是调整一下不会变差,而字典序变小了(所以要求字典序最小)。
于是我们知道,要求的这$n$条路径互不穿过,这称为路径不交性。
然后就有一个想法,我们随便选一个点开始,用前面的算法求一条路径,假设它是$p_0,…,p_k$,那么剩下的所有路径$q$,都要满足$q_i\in[p_i,p_{i+1}]$,否则就不满足路径不交性。
注意到这些区间的长度和只有$O(n+k)$!
此时我们可以想到一个暴力做法,这些段里面一定有一段长度是$\frac{n}{k}$以内的,并且不管在哪条最短路里面,这一段里一定要选一个点。不妨把它转成第一段,然后直接枚举这个第一个点,每次可以爆力$O(nk)$计算,总枚举量是$O(\frac{n}{k})$,乘起来我们得到$O(n^2)$。
另一种想法是,考虑进行分治,同时维护所有$k$个点的可能区间,每次在第一个区间里面取中点作为第一个点,然后依次在剩下$k-1$个区间里跑SMAWK得到一条最短路,并把这些区间劈开递归下去。
看起来这很像$O(n(\log n+\log v))$,但是实际上不是,因为 由于中点会同时递归到两边,每次劈开都会让总区间长度增加$k$,一共要劈开$n-1$次,最后一层的总区间长度会变成$O(nk)$,就死掉了。
怎么解决这个问题?如果我们可以让递归层数少一点,也就是让第一段长度小一点……考虑把$O(\frac{n}{k})$那一段转到第一段来做,这样会劈开$O(\frac{n}{k})$次,每次增加$k$个点,最后一共增加$O(n)$个点,这样复杂度就正确了,变成了$O(n(\log n+\log v))$。
SMAWK太难写了,我们可以换成分治,于是得到了$O(n\log n(\log n+\log v))$做法,可以通过。
呃等等,我们还没构造方案呢!
wqs二分在满足四边形不等式的DAG定长最短路问题中的快速构造方案
众所周知wqs二分的时候,如果遇到三点共线,那么各种奇技淫巧都难以搞到中间那个点,因此构造方案比较困难。一个可行的方法是爆力枚举第一段怎么选然后wqs二分剩下的,但是这样会让复杂度变得很劣。
不过我们有了上面的定理,就可以做一些很有意思的事情。我们跑两遍,一遍尽可能往左切,一遍尽可能往右切,就可以得到共线的左右端点,不妨设它们分的段数分别是$s,t$,那么显然$s<k<t$(如果有相等可以直接输出),于是我们可以采用刚才的定理构造出长$k$和$s+t-k$的路径。容易证明这条长$k$的路径就是长$k$的最优路径,所以我们就得到了答案。
四边形不等式旅行商
给一张完全图,它的邻接矩阵满足四边形不等式,解tsp。$n\leq 10^5$。
双调tsp
大家都知道双调tsp问题,毕竟这个在算导上作为例题。
啊你不知道?就是说,一开始一直往右走,走到头转而一直往左走,就叫双调;最后走回$1$就是双调回路;每个点都走一遍就叫双调tsp。
定理 四边形不等式旅行商问题一定存在一个最优解是双调的。
证明 归纳就行了。
$n\leq 3$的时候所有回路都是双调的。
考虑一个不是双调回路的最优回路,因为它不是双调的,一定存在一个点,使得回路中它前后的点编号都比它大,设这个三个点依次是$u,v,w$。
根据四边形不等式,我们知道$w(u,w)+w(v,v)\leq w(u,v)+w(v,w)$(注意$v<u,w$,而不是$u<v<w$),所以先把$v$拿出来自环,把$u,w$接起来形成总共两条回路,答案不会变差。
此时这条长$n-1$的回路,根据归纳假设可以换成另一条不劣的双调回路。
最后在换好的双调回路上找到相邻的$x,y$使得$x<v<y$,根据四边形不等式有$w(x,u)+w(u,y)\leq w(x,y)+w(u,u)$,所以就可以把$v$插回去,得到新的双调回路。
因为满足四边形不等式,双调tsp的dp还可以继续优化。
啊你说双调tsp的dp是什么?设$dp(i,j)$表示从$i$往$1$走,然后转而从$1$往$j$走的最短路径(因为从$n$走到$1$再回去,和从$n$走到$1$再回去都是双调回路)。转移只有$\vert i-j\vert=1$时需要枚举一个大的一边的前驱来转移,否则大的一边前驱是确定的,复杂度$O(n^2)$。
要优化,首先这个状态数太多了。我们可以只记录$f(i)=dp(i+1,i),g(i)=dp(i,i+1)$,然后打前缀和$sf(i)=sf(i-1)+w(i-1,i),sg(i)=sg(i-1)+w(i,i-1)$,考虑它们的转移 :
\[\begin{aligned} f(i)&=\min_{j=1}^{i-1}g(j)+sf(i)-sf(j+1) g(i)&=\min_{j=1}^{i-1}f(j)+sg(i)-sg(j+1) \end{aligned}\]你发现这个新的前缀和也是满足四边形不等式的,所以可以用二分栈来处理,或者直接Eppstein做到线性。
5.20 Open Cup趣题选讲
这个实在是毒瘤。jiangly眼中的趣题能不毒瘤吗/kel
Cactus Competition
给一个$n\times m$的棋盘,$(i,j)$的权值为$a_i+b_j$,其中$a,b$是给定的两数列。
求有多少对$s,t$满足存在一条从$(s,1)$走到$(t,m)$的路径(行从上到下,列从左到右标号),每一步只能往下或往右走一步,且经过的所有格子的权值非负。
$n,m\leq 2\times 10^5$,2s 1GB。
考虑$s=1,t=n$怎么做。
结论 : 可行,当且仅当下列所有情况都不存在 :
-
有一行不能走,也就是$\min a+\max b<0$
-
有一列不能走,也就是$\min b+\max a<0$
-
存在某一个格子$(x,y)$,它往上往左发射射线,射线经过的格子都不能走,把起点围住了。也就是对于所有$1\leq i\leq x,1\leq j\leq y$,都有$a_x+b_j<0,a_i+b_y<0$
-
存在某一个格子$(x,y)$,它往下往右发射射线,射线经过的格子都不能走,把终点围住了。也就是对于所有$x\leq i\leq n,y\leq j\leq m$,都有$a_x+b_j<0,a_i+b_y<0$
。如何证明?显然其中某一个出现的时候都不存在可行路径,所以我们只需要证充分性(都不出现则有可行路径)。
你发现如果前两个都不出现,就说明有至少一行一列全是可以走的,也就是$\max a,\max b$对应的行列。考虑它们的交点,设为$(x,y)$。
下面证明,从这个交点一定可以走到起点和终点,这两部分是类似的,所以我们只证可以走到起点。
画个图吧。绿色是可以走的一行一列 :
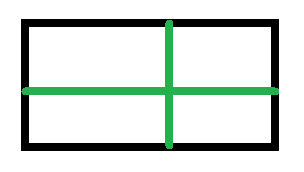
现在只考虑左上方这个小方格。如果存在一列全是可以走的(蓝色) :
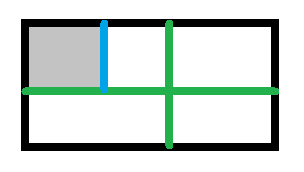
那么我们考虑这一列和刚才可以走的那一行框起来的区域(灰色),这是一个子问题。如果存在一行全是可以走的,情况类似。所以我们对这个进行归纳就可以了。
如果不存在这样的行或者列,容易想到我们要证明它一定不满足后两个条件。
你发现,不存在一行都能走,说明$\min b+\max a<0$(只考虑左上这个方格),说明$\min b$这一列就都不能走。同理,$\min a$这一行也不能走。我们取这一行一列的交点,就符合了上面的第三种情况,所以一定存在一行或者一列可以走。
好了现在我们得到了一个看起来很强的结论,怎么用它解决这道题呢?
先考虑第三个条件,它限制了一些起点总是不可行的,第四个限制了一些终点总是不可行的,除此之外没有其它的限制。考虑怎么预处理出来这些不可行的起点,终点类似。
呃考虑对于每一个$x$,求出从$(x,1)$往右,有多少个连续的格子是不能走的。然后从这一段连续不能走的某个位置,再尝试向上尽可能进行延伸,这样遮住的一个起点区间都不可行。再画个图 :

红色是连续不能走的,于是最高的那个ban掉了左边的一个起点区间。
这个东西怎么求?往右延伸可以搞一个前缀$\max$然后直接二分,往上延伸的话发现只有往右那一排的$\min$有用,可以用单调栈二分干掉。
然后问题是剩下的两个限制了。
一行都不行的话,相当于跨过它的区间都不行。
一列都不行的话,容易发现只需要考虑$\min b$那一列,然后对于一个ban掉的区间,相当于是让它对应的起点区间都不能走到它对应的终点区间。
你发现四种限制都是ban一个矩形,所以跑个并面积就好了。也有这一步线性的做法,不过没有必要。
复杂度是$O(n\log n)$。
Query on a Tree 17
树,根是$1$,支持链/子树加,查询最浅的带权重心。$n,q\leq 10^5$,2s 1GB。
以重心为根,每一棵子树大小都不超过一半,所以以$1$为根,带权重心的子树权值和至少是总权值和的一半(不然上面的子树就超了)。所以如果我们随便找一个dfs序,那么它的带权中位数一定在某个带权重心的子树里。
树链剖分,线段树维护dfs序来二分这个带权重心子树里的一个点。然后这个点上方第一个(最深的)子树权值和超过总权值一半的点一定是带权重心(它的儿子不可能是,它的父亲是的话它也是,而链上一定有一个)。
那最浅的怎么找?重心都是连通的,并且中间一定是有一些$0$权点,可以树剖支持跳一段$0$。复杂度是$O(n\log^2 n)$。
Steel Slicing 2
有一个奇怪的多边形,它由若干个从$x$轴上分别向上下延伸、宽度为$1$的矩形组成。你每次可以切一刀把这个多边形变成恰好两个多边形,求最少切多少次,使得切出来所有东西都是矩形。这个图看起来像是 :
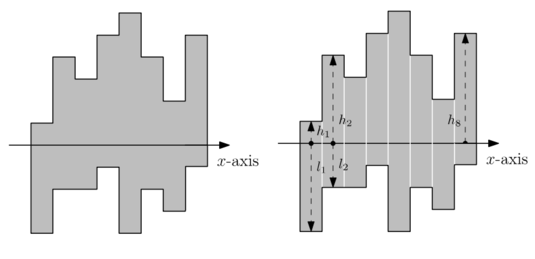
。$n\leq 2.5\times 10^5$,1s 1GB。
显然只会横着或者竖着切,那么切出来最后肯定都是方的东西,于是全是矩形等价于不存在凹的顶点。
发现每一刀肯定会让凹顶点数减少$1$或$2$,那么我们只需要最大化减去$2$的刀数。
刀们相互之间的影响只有 : 如果横着切了一个顶点,不能再竖着切,反之亦然。另外,如果横着切的时候跨过了一种竖着切的方案,那么这个竖着切的方案就变成了上下两个只能让凹顶点数减少$1$的方案,所以它也不能选了。
所以容易想到建立二分图,左右分别是横着和竖着切的方案,对于每一个横着切的方案,向它影响的竖着切的方案连边,求最大独立集。
竖着切很容易预处理出来会减去多少凹顶点,横着切可以用上下两遍单调栈处理出来,最大独立集等于点数减去最大匹配,所以已经可以爆力Dinic做到$O(n^{2.5})$了,因为边数很多。
不过这么多的边都有一个性质 : 每个横着切的方案,一定是向一个区间中竖着切的方案连边。
考虑贪心,我们从左往右枚举竖着切的方案,贪心地匹配右端点最靠左的横着切的方案(注意我们现在在求最大匹配),可以用堆维护。复杂度$O(n\log n)$。
Interesting Drug
数轴上有$n$个东西,分别在$1,…,n$。你可以选择从任何一个点出发,然后可以左右移动,如果你走到一个东西,你就必须拿走它。有两个长$n$的数组$c,d$,表示如果物品$i$是第$c_i$个拿走的,你可以得到$d_i$的收益。对于每个起点坐标,最大化取得所有物品的收益。$n\leq 3\times 10^5$,$d$非负。
这种在数轴上往左往右走拿东西的问题,任意时刻拿到的东西一定是一个区间。设$dp(i,j)$表示拿了区间$[i,j]$中的物品得到的最大收益,决策最后拿最左边还是最右边进行转移即可。这样爆力就可以做到$O(n^3)$。
每个点开始跑一遍太恶心了,我们重新设$dp(i,j)$表示已经拿了$[i,j]$,拿完剩下的东西得到的最大收益,这样可以只跑一遍dp,复杂度是$O(n^2)$。
优化比较有意思。这个问题可以抽象成在平面上从$(1,n)$开始走,每次可以从$(x,y)$走到$(x+1,y)$或者$(x,y-1)$,也就是向右或者向下走一步。每一次有权值的转移都可以看成一条边,这样的边数量只有$O(n)$,我们可以从上往下扫,用BiT批量转移,就做完了。复杂度$O(n\log n)$。
Find the LCA
给一个长$n$的点权序列$a$,对于所有 给每个点在它前面找一个父亲 而生成的有根树,求$\mathrm{lca}(n-1,n)$子树内所有点点权乘积的和。$n\leq 2.5\times 10^5$,7s 1GB,膜$998244353$。
XXI Open Cup. Grand Prix of 998244353, Problem F(这一场十个题全是膜$998244353$/jy)
考虑对于一个点集$S$,求出$\mathrm{lca}(n-1,n)$恰好是$S$的方案数。
如果$1\in S$,那么$S$一定是$1,2,…,n$;否则,$S$之外的点只能向$S$之外连边,$S$里面的最小值(也就是根)可以在前面随便找父亲,这两部分是$(n-\vert S\vert-1)!(\min S-1)$;然而把$S$内部拼成一棵树的方案数就不是那么显然。
你发现这里有一个子问题,我们设$f(n)$表示$n$个点的树,$\mathrm{lca}(n,n-1)=1$的方案数。那么上面的那个把$S$内部拼成一棵树的方案数,重标号一下,就变成了$f(\vert S\vert)$。
结论 $f(n)=\frac{1}{2}(n-1)!$,也就是这样的树恰好占一半。
证明 打表容易发现。jiangly给出了一个双射法的证明,有点阴间。
考虑对于一棵$\mathrm{lca}(n-1,n)=1$的树,我们把$1$的子树们中包含$n-1$的那个设为$x$,然后把$x$的子树取出来插入$1$到$n$的路径(因为父亲比儿子小,只有一种插法),这样就得到了一棵$\mathrm{lca}(n-1,n)=x$的树。
反过来,我们找到$x=\mathrm{lca}(n-1,n)$,取出$x$和它不包含$n$的子树们,一起接到$1$上,然后把包含$n$的子树接到原来$x$的父亲上,就得到了一棵$\mathrm{lca}(n-1,n)=1$的树。
于是我们得到了一个双射,这确实很双射。
剩下的部分就很简单了,因为一个集合的贡献只和它的大小和$\min$有关。我们枚举集合大小$k$,然后把那个连到外面的系数扔掉,问题变成求$\sum_{\vert S\vert}=k(\min S-1)\prod_{i\in S}a_i$。
啊如果没有这个$\min$大家都会做,直接分治法法塔即可。
有了$\min$也可以分治法法塔!分治的时候同时维护 答案 和 不考虑$\min$的答案,然后你发现一个区间的答案可以用 左区间的答案乘右区间不考虑$\min$的答案 加上 右区间的答案 得到,于是做完了。复杂度$O(n\log^2 n)$。
Japanese Knowledge
如果Japanese Knowledge指的是分治法法塔,这题的核心可不是Japanese Knowledge/kk
给一个单调递增序列$a$,对于所有$0\leq k\leq n$,求满足
-
$x$单调递增,
-
$x_i\leq a_i$,
-
有恰好$k$个下标满足$x_i=a_i$
的序列$x$数量。$n\leq 2.5\times 10^5,a_i\leq 2.5\times 10^5$,20s 1GB,膜$998244353$。
设$f_k(a)$表示懂的都懂,$g(a)$表示不考虑$k$的答案。
容易给$f_k(a)$一个简单的折线解释,就是从$(1,0)$走到$(n,…)$,每一步往右或往上走,不越过$(i,a_i)$,并且恰好与$(i,a_i)$有$k$次重合的方案数,意义是每一个$x=i$上走过的最高的点表示$x_i$;$g$的话就没有那个$k$次重合的限制了。
不过$(n,…)$有点恶心,我们加一列,变成走到$(n+1,a_n)$,这样就很舒服。
呃然后你发现可以平移,我们改成从$(0,0)$走到$(n,a_n)$,把限制改成$(i-1,a_i)$,每一个$x=i-1$上走过最高的点表示$x_i$,这样就更舒服了。
下面考虑一个无敌双射。
问题1 : 现在给定了一个01操作序列$x$。你有一个栈$s$,从前往后扫过操作序列,遇到0则push一个元素,遇到1则pop若干元素(可以不弹)。称一次操作1是好的,当且仅当弹完之后栈空,问有多少种方案使得恰好有$k$次好的操作1。元素都是可区分的,两个方案不同当且仅当在一次1操作中pop掉的元素不同。
容易发现我们这样构造$x$ : 对于每个$i$,放$a_i-a_{i-1}$个0操作,然后放一个1操作,此时问题1就等价于计算$f_k(a)$。
为了推出一个很好玩的结论,我们进行时间倒流(怎么想到的),并交换两种操作的地位(又是怎么想到的)。
问题2 : 现在给定了一个01操作序列$x$。你有一个栈$t$,从后往前扫过操作序列,遇到0则pop若干元素(可以不弹),遇到1则push一个元素,问有多少种方案使得最后剩下恰好$k$个元素。元素都是可区分的,两个方案不同当且仅当在一次0操作中pop掉的元素不同。
这里对$t$的意义给出解释 : 它维护的是$s$中可能好的1操作。问题2中对于一次0操作,如果它弹掉了某个1操作,含义是在问题1中,这个1操作执行之后,这个0操作还在栈里,于是这个1操作不可能是好的。仔细想一想你发现它们之间确实建立了某种双射。
然后考虑问题2的组合意义。把上面的操作序列反过来就是对于每个$i$(从大到小),放一个1操作,然后放$a_i-a_{i-1}$个0操作,然后我们把问题2变成正着扫,这样就舒服一点。
折线。你发现这个放一堆$0$就让我们没法直接折线解释这个东西了,不过我们可以先用一个隔板解释它,然后尝试把它转成折线。如果要在一串$m$个0操作中pop $t$次,方案数就是$\binom{m+t-1}{m-1}$,也就是从$(0,0)$走到$(m-1,t)$的方案数。这就很好!
既然我们刚才把pop当成往上走,听起来把push当成往右走更靠谱。你画一画会发现,它走出来的可行区域大概是这样(折线上面是每一段的长度,下面是点的坐标) :

然后考虑最后的情况。如果我们从$(0,0)$出发,要留下$k$个元素,最后就应该走到$(n-k,a_n)$,或者说我们不能越过$y=n-k$,相当于最后的$k$个元素消失了(倒过来的最后$k$个,正着看的开始$k$个)。
把这个区域倒过来看,你发现它恰好就是$g({a_{k+1}-1,a_{k+2}-1,…,a_n-1})$。这可真是太**奇妙了!
然后就可以考虑怎么算$g$。相当于给一个看起来像杨表的东西,要对于下边每一个点,算从它出发,每一步可以往右往上走,走到右上角的路径数量。
我们考虑一个过程solve(l,r,L,R),表示给出从$(r,L),(r,L+1),…,(r,R)$(右边界)出发的答案,计算从$(l,L),(l+1,L),…,(r,L)$(下边界)出发的答案。
进行分治。选取中点$mid$,从$(mid,a_{mid})$往右往下画射线,把这个东西分成三部分,之后每一条路径只可能是
-
左下->右下->右上
-
右下->右上
-
右上
。先递归右上,然后通过右上部分下边界的答案计算左下部分右边界的答案,然后递归左下。右下部分是一个长方形,贡献可以容易地用组合数表示,显然是一个卷积的形式,我们用法法塔优化,就做完了。
呃复杂度?每层的$R-L$之和是$O(n)$的,所以每层的法法塔一共是$O(n\log n)$,一共有$\log n$层,所以复杂度是$O(n\log^2 n)$。
Chess Tournament
有一场大赛,有$n$位选手要两两进行一场比赛。大赛进行若干轮,每一轮最多有$k$场比赛,并且一名选手不能在一轮中参加多于一场比赛。构造一个方案使得比赛轮数最少。$n\leq 200,k\leq\frac{n}{2}$,2s 512MB。
强行构造。这个题的方法是,第$i$轮尝试让每一对到$i$距离相等的人比赛,这里的距离是按照环算的。
然后你发现如果$k=\lfloor\frac{n}{2}\rfloor$,那就构造完了,因为每一轮确实都可以这么搞。
我们观察上面构造的性质,发现如果按照上面所说的 距离 来对每一轮的比赛排序,每个人上一轮和这一轮的比赛在轮中的排名至多相差$1$,所以如果把这些轮直接接起来,一个人不可能在相邻的$\lfloor\frac{n}{2}\rfloor-1$场比赛中出现两次,按此构造对$k<\lfloor\frac{n}{2}\rfloor$是一定可行的。
呃最优性显然,你的比赛都排满了,怎么可能不是最优?
5.21 组合计数问题的常用技巧
CF1264D2 Beautiful Bracket Sequence
考虑把括号序列看成折线,那么要找子序列最大值,我们贪心地一定是找一个单独的”山峰”,因为在任何方案中,去掉最高峰之外的部分都不会影响答案。
所以对于一个没有?的串,我们dp一遍找到最高峰就好了。
一种听起来更直接的方法是,我们枚举这个峰顶(可能有不止一个),然后找到左边有多少左括号,右边有多少右括号,取个$\min$更新答案。
然后你发现这是一个前缀和和一个后缀和的$\min$,并且这两个和每走一步一定有一个改变,所以我们知道这个峰顶实际上只可能有一个,并且在这个位置有左右左右括号数量相同,而其它所有位置都没有。
所以我们已经把每个子序列最大值对应到了唯一的一个位置,这就非常好。
对于原问题,我们还是枚举这个位置,统计有多少种方案让它左右两边左右括号数量相同。这个可以通过一个组合数轻易地选出来,做完了。
CSP-S2019 Emiya家今天的饭
童年阴影/ll
写过了诶。
AGC052C Nondivisible Prefix Sums
这就是AGC吗/jy
你咕没有题意翻译(,甚至没有题),这里写一下吧……有一个你不喜欢的质数$p$,定义一个序列是好的,当且仅当把它以某种方式重排之后,每个前缀和都不是$p$的倍数。求有多少长度是$n$、每个值在$[1,p-1]$中的好的序列。$n\leq 5000,3\leq p\leq 10^8$,2s 1GB,膜$998244353$。
考虑还是找一堆必要条件,最后得到充要条件。
首先不管怎么重排,总和是不变的,所以总和不能是$p$的倍数。
然后考虑一个简单的构造,我们从左往右扫,每次遇到前缀和要变成$p$的倍数了,比如当前扫到的是$x$,我们就从后面随便找一个$y\neq x$,然后把这俩换一换。
这个构造什么时候会死?只可能是,$cur+x$是$p$的倍数,但是剩下的只有$x$了。
这说明$x$太多了,于是我们希望让每种数都不那么多。可以这样搞 : 我们从左往右往序列里扔东西,每次找到当前剩下最多的数$x$,假设前缀和是$cur$,如果$cur+x$不是$p$的倍数,我们就放一个$x$,否则随便找一个$y\neq x$,放一个$y$,再放一个$x$。这样至少每两次可以干掉一个$x$。
不过这个还是会死 : 众数$x$出现次数超过一半,剩下的数全是$y$,并且$x+y=p$。呃反过来,我们知道,众数出现次数不超过一半,我们的构造就是有效的。
然而这个条件并不必要,不过现在至少我们知道这个问题很可能跟众数$x$有关了。
标准化。因为$p$是质数,我们知道$[1,p-1]$中每一个数在这个问题中都是平等的,不妨把整个序列乘上$x$的逆,这样$x$就全变成$1$了,而一个序列是否是好的这件事显然是不变的。接下来只需要考虑众数是$1$的情况。
众数出现最多多少次,我们的构造才有效?你发现根据我们上面的hack,这个次数不只跟$n$有关,还跟序列中其它的数有关,于是假设删掉$1$后我们得到序列$b$,它的长度是$k$。
为了尽可能多地放$1$,我们有一个贪心策略 : 一开始可以放$p-1$个$1$,然后每次放一个$b_i$,都可以接着放$p-b_i$个$1$把前缀和填回$p-1$。所以我们至少可以放$p-1+\sum (p-b_i)$个$1$。下面证明这就是最多的,并且放的$1$在这个数量之内则一定可行。
必要性 : 考虑如果可以放的比这个多,首先放$p+\sum (p-b_i)$个$1$显然是不可行的,因为此时序列的总和会变成$(k+1)p$。所以我们一定放了至少$p+1+\sum (p-b_i)$个$1$,此时总和是$(k+1)p+1$,也就是说总和以内的$p$的倍数有$k+1$个,而每一个$b_i$可以用来”跨过”最多一个$p$的倍数,那么一定有一个是跨不过去的。
充分性 : 我们上面的构造算法中,容易发现如果$1$一开始是众数,那么接下来剩下的$1$的出现次数比众数少不超过$1$,这说明最后如果有剩下超过一个相同的数导致算法死掉,它们一定是$1$。
先证明如果只剩下一个数,那么算法不可能死。呃因为总和不是$p$的倍数,直接放就好了,所以这是两句废话。
然后如果剩下了一堆$1$,你发现前面得到的序列就跟刚才我们贪心放$1$得到的序列是一样的了,所以我们应该可以干掉所有$1$的。
于是就证完了。接下来用总和不是$p$倍数的方案数,减去$p-1$倍的总和不是$p$倍数、并且$1$出现次数超过上面那个东西的方案数。这个$p-1$是为了把$1$映射到所有可能的众数。
第二个方案数可以用dp解决。我们对删掉$1$得到的序列$b$计数,设$dp(i,j)$表示放了$i$个不是$1$的数,算出来最多可以放$j$个$1$的方案数,当这个$j>n$的时候可以统一扔进一个状态$dp(i,n+1)$(所以刷表更舒服)。转移枚举这一位放什么,有这样的式子 :
\[dp(i+1,j+p-k):=dp(i+1,j+p-k)+dp(i,j)\]。发现是一个后缀加,可以打标记然后前缀和一下进行优化,非常简单。剩下的工作也非常简单了,于是总复杂度是$O(n^2)$。
AGC012F Prefix Median
考虑直接去重听起来非常恶心,我们试着干这么一件事 : 给你一个序列$b$,试图通过调整$a$把它构造出来。
从左往右扫$b$。如果$b_i$还没被放进$a$,那就把它放进去;然后在还没放的数中找最大/最小值放进去来调整,因为中间的数放进去可能会产生一些影响,两边的数则不会,因为两边的数已经不可能成为中位数了。
于是我们可以得到一组必要条件 :
-
每个位置需要在它的上下界里。上界就是放的时候全放大的得到的序列,下界相反。
-
不存在$j<i$满足$b_{i-1}$到$b_i$跨过了$b_j$,也就是不可能一次调整两步。
根据上面的构造容易证明这也是充分条件,所以问题就变得比较简单了。
然后我们就可以硬算这样$b$的数量了。
不能跨过前面的数 这个东西似乎有点难受(不过实际上可以接受?),进行时间倒流,变成 不能把一个数插在后面两个数之间,也就是跨过的数都不能选了。
显然可以搞dp了。设$dp(i,j,k)$表示考虑$i$和之后的数,还有$j$个可以用的数,这一个选的是其中第$k$小的方案数。转移枚举上一个选了什么,复杂度$O(n^4)$。
AGC043D Merge Triplets
考虑这个归并排序是在干什么。
你发现它相当于把每个串按照前缀最大分成若干段,每一段从这个前缀最大值到下一个前缀最大值之前,然后把这些段按照它们的第一个数排序接起来。
所以,容易想到一个排列可以搞出来的一个必要条件 : 按前缀最大值分段,它的每一段长度都不超过$3$。设三种段的数量分别是$c_1,c_2,c_3$。
显然还有另一个条件 : 每一个$2$都要配一个$1$,所以$c_2\leq c_1$;总长度是$c_1+2c_2+3c_3=3n$。
它充分吗?直接构造就是了,显然充分。
然后就可以做一个背包,设$dp(i,j,k)$表示$1,…,i$的序列,$c_1=j,c_2=k$的方案数,当然此时$c_3=i-\frac{1}{3}c_1-2c_2$。转移就枚举选$1,2,3$中的哪一种,注意到最后一段的第一个一定是整个序列的最大值$i$,所以可以组合数选一选选出来。
这么做是$O(n^3)$的,不过注意到实际上$c_1,c_2,c_3$的值并不重要,只有$c_1$和$c_2$的大小关系有用,所以可以进行差值优化。改设$dp(i,j)$表示$c_1-c_2=j$的方案数,转移还是一样的,就是$O(n^2)$了。
差分
有一个很有意思的式子 : $x=\sum_{i=1}^x 1$。这个式子可以帮我们做这么一件事 : 枚举$i$,然后我们就只关心$i$和$x$的大小关系了。
WC2021 表达式求值
草,童年阴影/ll
容易发现每一个位置是独立的,可以拆开。
注意到最后得到的数一定是操作数中的一个,考虑直接对于每种可能的大小关系预处理答案是哪一个,不过$10!$太大了,会T飞。
如果可以把$10!$变成$2^{10}$就很好,所以我们枚举一个$i$,用上面的式子搞一搞。相当于把所有数变成$0/1$,然后求答案是$0$还是$1$。这是预处理。
对于每一个位置,从小到大枚举$i$,发现把数放到数轴上之后,每一段的情况都是一样的,可以直接查表查出来然后乘上长度。就做完了。
呃这个题有一些等价的思考方式,不过差分也很好想。
配凑
有些东西看起来就很像另一些东西的样子。例题吧。
ARC082E ConvexScore
你发现这个贡献非常有意思。它就是对于凸包内的点集的子集数。所以问题变成了,有多少点集二元组$(S,T)$,使得$S$是凸包,$T$与$S$不交,并且$T$被包含在$S$内。
你发现$T$与$S$不交就很好。我们考虑$T\cup S$,你发现这个$T\cup S$它的凸包是唯一的,也就是说如果我们知道$T\cup S$,那么$S$是唯一的,同时$T$也是唯一的。换句话说,一个点集和它的凸包和它里面凸包之外的部分是对应的。这就非常好,所以答案就是$2^n$?
然而不是,因为$T\cup S$还可能没有凸包。所以我们枚举一条直线,计算多少点集没有凸包,用$2^k$减去这个东西就是答案了。
十二省联考2019 希望
/jk/jk/jk/jk/jk/jk/jk/jk
一个经典容斥技巧,说的是非空树满足$v=e+1$,而空树有$v=e=0$。这是一句废话,但是在这道题里特别有用。
如果固定了所有的救援范围,合法的发动机可能不止一个,这让我们没法枚举发动机统计答案;但是显然一定是一个连通块。
利用上面的容斥,我们知道如果这个连通块非空那么$v-e=1$,否则$v-e=0$。也就是说我们枚举所有点统计这个点包含于某个连通块的答案,然后枚举所有边再统计一遍,用第一个减去第二个,那么每种救援范围就恰好被算了一次。
然后就是一个简单dp。搞一个$t(u)$表示到$u$距离不超过$L$的连通块个数,那么$(t(u))^k$就是上面要算的第一个东西,第二个东西类似。
问题变成怎么算$t(u)$。先考虑一个爆力dp。
为了方便计算边的贡献,我们设$f(u,i)$表示$u$子树内距离不超过$i$的答案,$g(u,i)$表示$u$子树外的答案(呃都强制选$u$),然后点和边的贡献都可以这样求出来,就得到了一个$O(n^2)$做法。
然后我们就可以长链剖分优化这个东西,具体细节非常繁琐,我就不提了/hanx(这才是重点吧啊喂
NOI2018 冒泡排序
考虑一个排列在什么情况下达到交换下界,根据tips应该是每次都减少两次需要的移动。
于是我们知道,每次交换两个数,它们都应该是向着正确的方向。
于是,我们知道,如果一个数应该往右移动,那么它左边所有数都应该比它小;如果一个数应该往左移动,那么它右边所有数都应该比它大。这样两边的数才不会影响它的移动。
考虑一个数$j$和它左边的$i$、右边的$k$,如果$j$应该往右走,那么$a_i<a_j$;如果$j$应该往左走,那么$a_j<a_k$。如果这两个都不满足,也就是$a_i>a_j>a_k$,或者说存在长为$3$的下降子序列,我们可以断言这个排列一定不好。但是这充分吗?或者说如果没有同时不满足这两个条件的三元组,就一定好吗?
呃你可以通过打表或者什么别的方式发现确实可以。一个简单的证明是,容易发现如果一开始不存在这样的三元组,因为冒泡排序不会增加逆序对,每次交换之后仍然不存在这样的三元组。然后你发现每次交换一定是减少两次需要的移动,所以就得证了。
问题变成计数多少排列不存在长为$3$的下降子序列,且字典序大于$q$。
先考虑没有字典序限制怎么做。
手玩一点,你发现这么一件事,是说如果从左往右填,你每次要么填一个比之前填的最大值更大的数,要么填之前没填过的最小的数。所以可以写出一个dp,设$dp(i,j)$表示填了$i$个数,之前填的最大的是$j$的方案数,转移只要在这两种中决策选哪个即可,注意$i=j$是特殊的,它的第二种决策要并入第一种决策。然而如果你实现一下或者随便想一想就会发现,$dp(i,i)$直接转移会到$dp(i+1,i)$,我们不处理$dp(i+1,i)$这种东西就好了。
然后考虑优化。要想优化,我们需要先看看式子到底是什么 :
\[dp(i+1,k):=dp(i+1,k)+dp(i,j)\]你发现像极了格路计数!可以解释成,从$(0,0)$出发,走到$(n,n)$,第一步必须往上走,不能穿过$y=x$的路径数。这似乎确凿就是Catalan数。
然后来处理这个字典序,容易想到枚举$k$,让前面$k-1$项和$q$相同,第$k$项更大,之后随便填。
然后你发现相当于换了一个起点,答案就是$(k,\max_{i=1}^k q_i+1)$,翻折法随便算即可。复杂度$O(n)$。
啊你说怎么翻折?考虑从$(i,j)$走到$(n,n)$且不越过$y=x$的话,对于不合法路径我们找到和$y=x-1$的第一个交点,并关于$y=x-1$对称,起点变成了$(j+1,i-1)$,然后不合法路径就和$(j+1,i-1)$到$(n,n)$的路径建立了双射。总路径数是$\binom{n-i+n-j}{n-i}$,不合法的是$\binom{n-i+n-j}{n-i+1}$,两个一减就是答案。
AGC041F Histogram Rooks 加强版
$n\leq 2000$。
显然要容斥。钦定一些格子不被覆盖,那么和它同行或者同列的格子都不能放车,其它格子随意,方案数就是$2^\text{没有限制的格子数量}$。
这个东西据说可以直接dp,但是我不会/cy
注意到行可能被障碍分成若干段(呃这个还有用,每一段我们称为一个行连续段),但是列不会,所以如果一列被钦定了一个格子,那么整列都不能放车了,行则没有这样的性质。这启发我们按列为状态设计dp进行优化。
考虑枚举一个列的集合$S$,计算 这些列就是钦定的格子所在的列 时的贡献。注意这个 就是,它说的是一列不多一列不少。
对于一个行连续段,假设它的长是$l$,有$p$个位置和$S$中的列有交,那么
-
如果这个行连续段没有钦定的格子,那么有$l-p$个格子都可以随便放,贡献是$2^{l-p}$。
-
否则,一个车都不能放,但是还是对容斥有贡献。枚举有多少个钦定的格子,用组合数选出来,贡献是$\sum_{i=1}^p(-1)^i\binom{p}{i}=[p=0]-1=-[p\neq 0]$。这个式子怎么来的?非常经典,呃实际上它就是二项式定理$(1+(-1))^p$。
然而这个东西不是很对,因为这样搞完之后,我们枚举的列集合不一定每一列都有钦定的格子,这就很不好。
这是最关键的一步 : 继续容斥。我们对 每一列都有钦定的格子 进行容斥,枚举一个集合$T$,表示上一步选出来的没有钦定的格子的列。
对于一个行连续段,假设它的长是$l$,有$p$个位置和$S$中的列有交,有$q$个位置和$T$中的列有交,那么
-
如果这个行连续段没有钦定的格子,那么有$l-p$个格子都可以随便放,贡献是$2^{l-p}$。
-
否则,一个车都不能放。枚举有多少个钦定的格子,用组合数选出来,贡献是$\sum_{i=1}^{p-q}(-1)^i\binom{p}{i}=[p-q=0]-1=-[p-q\neq 0]$。注意到$p\geq q$,所以$-[p-q\neq 0]=-[p>q]$。
然后它就很对了。接下来考虑dp优化这个东西。
dp的转移结构,当你看到这个题的棋盘的时候就很显然了 : 笛卡尔树。
我们每次找到最小值,从它画横线把下面的长方形切掉,然后递归上面的部分(可能不止两边,因为最小值可能不唯一)。设$dp(i,j,0/1)$表示在结点$i$,有$j$列在$S$中,在$T$中的$=/>$在$S$中的,所有方案的贡献和。卷一卷,然后多考虑额外的部分就好了,这是一个长方形所以很好处理。复杂度是树卷积的$O(n^2)$。
这题打算写一写,因为感觉理解很不深刻 qwq
5.22 根号科技
认为$q$是操作数,$m$是别的一些东西。
设每$K$个操作分一块,那么一共有$B=\Theta(\frac{q}{K})$块。
APIO2019 桥梁
连通性显然并查集。
如果没有修改,可以离线下来,按照边权排序加边,并查集维护连通性。
发现如果修改很少,可以先按照边权排序所有没被修改的边和查询,每次扫到一个查询,就加入它前面所有的被修改的边(这个前面是时间上的前面),求出答案之后撤销回去。不考虑排序,这个复杂度是$O(cq\log n)$,其中$c,q$分别是修改和查询的个数。
考虑对操作进行分块。每一块都需要先用并查集搞出前面边的连通性信息,这个复杂度是$O(mB\log(n))$;每个询问需要遍历同一块的$O(K)$个修改,这个复杂度是$O(qK\log n)$。取$B=\Theta(\sqrt{n})$,可以得到复杂度是$O(q\sqrt{m}\log n)$。
这题的启发是,当静态问题和修改很少的问题都可以随便做的时候,可以考虑对操作序列分块,或者说对时间分块。
2017-2018 ACM-ICPC, NEERC, Northern Subregional Contest Problem J. Joker
给一个每一项都非$0$的序列$a$,设其中所有正数的和是$P$,负数是$N$。对于每个$a_i$如果$a_i>0$,令$w_i=\frac{a_i}{P}$,否则$w_i=\frac{a_i}{\vert N\vert}$ 。令$s$是$w$的前缀和,每次对$a$单点修改,求$s$的下标最小的最小值。$n,m\leq 5\times 10^4$。
除一个东西就很不好,我们乘回去。设$v_i=w_i\times P\times\vert N\vert$,$t$为$v$的前缀和。
观察$v,t$的形式,它们是
\[\begin{aligned} v_i&=\left([a_i>0]\frac{a_i}{P}+[a_i<0]\frac{a_i}{\vert N\vert}\right)P\vert N\vert=[a_i>0]a_i\vert N\vert+[a_i<0]a_iP\\ t_i&=\sum_{j=1}^i\left([a_i>0]a_i\vert N\vert+[a_i<0]a_iP\right)=\vert N\vert\sum_{j=1}^i[a_i>0]a_iP\sum_{j=1}^i[a_i<0]a_i \end{aligned}\]好像看到了一个凸壳。我们构造$p_i=([a_i>0]a_i,[a_i<0]a_i)$,那么上面那个东西就相当于从每个点出发画一条直线$\vert N\vert x+Py=c$,要最大化$c$。
最大值一定在上凸壳上取到,并且求出凸壳就可以二分,所以变成了动态维护一个前缀和的凸壳。
首先有一个很好的性质,就是在某个区间前面做了修改的话,相当于对这个区间整体平移,所以这个区间的凸壳上的点集不会改变。
你发现线段树平衡树什么全死了,我们来分块。
单点修改就把被改的插排回去并重构这一块的凸壳,这个复杂度是$O(K)$。查询的话每一块二分一次,是$O(B\log n)$。
取$K=\Theta(\sqrt{n\log n})$的时候最优,复杂度是$O(q\sqrt{n\log n})$。
这个问题的启发是,修改时只能重构,并且重构和查询复杂度不平衡,贡献可快速合并,就可以考虑分块来平衡复杂度。
UNR#4 己酸集合
给一个点集,每次给出以$(0,z)$为圆心,半径是$r$的一个圆,查询这个圆里面的点数。$n\leq 1.2\times 10^4,q\leq 10^6$。
这题一看就很离谱。先推个式子。
\[\begin{aligned} x^2+(y-z)^2&\leq r^2\\ x^2+y^2-2yz+z^2&\leq r^2\\ -2yz+x^2+y^2\leq r^2-z^2 \end{aligned}\]把每个点看成直线$f(t)=-2yt+x^2+y^2$,询问看成点$(z,r^2-z^2)$,问题就变成查询一个点下方的直线数量。
你发现任意两条直线最多只有一个交点,所以从左往右看,它们的大小关系最多变化一次,那么$n$条直线最多变化$O(n^2)$次。预处理这些变化,每次变化的时候交换两条直线的位置,然后对于每个查询二分一次,这就是$O(n^2\log n+q\log n)$的暴力(其中$n^2\log n$上的$\log$是对交点排序的复杂度)。
发现$n,q$上的复杂度很不平衡,考虑分块。把直线们每$B$个一组,那么每组的复杂度就是$O(B^2\log n+q\log n)$,取$B=\Theta(\sqrt{q})$的时候平衡,复杂度是$O(n\sqrt{q}\log n)$。
集训队互测2018 完美的队列
有一排队列,每一个都有一个大小上限$a_i$,当大小超过上限的时候会自动pop到上限以内。支持区间push一个$x$,然后查询全局所有队列中不同的元素数量。$n,q\leq 10^5$。
考虑对于每个操作,求出它插入的元素什么时候全被弹掉,这样就可以扫一遍求出答案了。我们称一个操作失效,当且仅当它插入的元素弹空了;失效时间是第一个失效的时间。
爆力怎么做?先枚举一个操作。假设要处理操作$i$,那么它插入到队列$j$的元素,将在接下来第$a_j$次操作的时候被弹掉。扫过它后面的操作,对于每个队列维护还需要加多少次就可以弹掉操作$i$插入的东西了。这个东西复杂度是$O(ql_i)$,其中$l_i$当然是$i$操作的区间长度。可以用线段树优化掉那个$l_i$,不过下面我们并不需要这么做。
容易发现一个性质 : 如果两个操作的区间相同,那么先进行的操作不会后失效(但是好像可能同时失效)。对于区间相同的所有查询,我们可以用双指针扫一遍,一口气求出它们的失效时间。
可以考虑线段树,把每个操作挂到线段树上拆成$\log$个区间,然后对于每个结点双指针一遍处理它上面的操作,复杂度是……$O(nq\log n)$?原因是我们双指针的时候每个点都需要处理$O(q)$个可能覆盖这个点的询问。
所以考虑分块,降低处理的次数。
整块套用刚才的爆力,复杂度是$O(q(B+K))$……吗?你发现一个操作可能覆盖很多整块,而每一块上都需要处理它的影响,这就爆炸了。我们对上面的爆力作一点修改,每次扫到一个覆盖了这个块的操作,不进行爆力重构,而是打一个标记。这样每个询问只会在左右零散部分被处理,复杂度就正确了。
零散部分则比较难办,因为我们不能扫整个操作序列了。不过注意到覆盖某个整块的操作,对于这个整块里面的点贡献是相同的,所以可以按照不完全覆盖这个块的操作来给时间分成若干段,对于每一段预处理出其中完全覆盖这个块的操作的贡献(实际上一定是一个全局标记),接下来只要在分段点上做双指针就好了,总复杂度是$O(q(B+K))$。显然取$B=\Theta{\sqrt{n}}$,复杂度是$O(q\sqrt{n})$。
回滚莫队
序列,每次查询区间最大的$a_i-\mathrm{pre}(a_i)$,其中$\mathrm{pre}$是前驱。$n,q\leq 10^5$。
好像很经典啊/kk
好像还有什么主席树2log做法,打算写最后也没写(
回滚莫队(不插入)说的是,把序列分块,把每个询问插入左端点对应的块中,按右端点从大到小排序。
枚举每个块$[L,R]$,处理它的询问。一开始预处理$[L,n]$的信息;假设现在处理询问$[l,r]$,那么我们先缩小$R$到$r$,然后缩小$L$到$l$。因为左端点没有单调性,求出答案之后我们需要把$L$扩大回去。注意这里是 回去,所以不需要支持插入,只需要支持撤销。
不删除也好办,把上面的过程反过来就行了。
莫队二次离线
线性空间区间逆序对
莫队。
线性空间的话,硬转移是不行了(需要开可持久化值域分块),考虑能不能用某种别的方式求出一串连续转移的贡献。以一连串右端点右移为例,假设要从$[l,r]$到$[l,r^\prime]$。
设$f$是区间逆序对。考虑给$f(l,r)$拆前缀和,它就是$f(1,r)-f(1,l-1)-g(1,l-1,l,r)$,其中$g(l_1,r_1,l_2,r_2)$表示$i\in[l_1,r_1],j\in[l_2,r_2]$的逆序对$(i,j)$数量,也就是$[l_1,r_1]$对$[l_2,r_2]$的贡献。
考虑转移的贡献,有$f(l,r^\prime)-f(l,r)=f(1,r^\prime)-f(1,l-1)-g(1,l-1,l,r^\prime)-f(1,r)+f(1,l-1)+g(1,l-1,l,r)=f(1,r^\prime)-f(1,r)-g(1,l-1,r+1,r^\prime)$。
前缀逆序对数容易BiT随便算,问题变成求$O(q)$个$g$。注意到要求的$g$的$l_1$全是$1$,所以可以把每一次求$g$挂到$r_1$上去。
注意到莫队的正确性在于所有$r^\prime-r$的和是$O(n\sqrt{q})$的,所以我们可以对于每次求$g$爆力枚举$i\in[l_2,r_2]$。容易使用BiT维护,但是复杂度会多一个$\log$。
注意到只有$n$次插入,但是查询有$O(n\sqrt{q})$次,所以可以上一个根号平衡。注意这里不需要可持久化了,所以空间就是线性了,所以就做完了。
hdu6756 Finding a MEX
给一张图,支持修改一个点的点权,或者查询一个点邻接点中点权的$\mathrm{mex}$。$n,m,q\leq 10^5$。
图上邻接点,根号分治。小点容易维护,大点怎么做?
BiT爆力会多$\log$,所以考虑根号平衡,用一个值域分块来维护就可以了。
LCS
给一排串,每次查询两个串的最长公共子串长度。$n,\sum\vert s\vert,q\leq 10^5$。
根号分治。长串之间可以SAM爆力,长串和短串也可以SAM爆力,短串之间可以问到再跑。$O((n+q)\sqrt{\sum\vert s\vert})$。
THUPC2021初赛 区间众数
给一个序列$a$,每次查询一个区间$[L,R]$中有多少子区间$[l,r]$满足
-
长度是奇数
-
$\frac{l+r}{2}$是它的一个众数
。$n\leq 5\times 10^5,q\leq 10^6$,8s 256MB。
lxl : thupc有什么有趣的数据结构题吗
瞬间。。 : 那个I题好像是数据结构题(笔者 : 好像是I,我已经忘记了)
lxl : 说说题意
…
lxl : 这题我出的啊
离线,枚举一个区间中点$p$,考虑$[p-k,p+k]$们的贡献,也就是这里面哪些区间以$p$作为众数。
你发现一件事情,如果$p$出现$c$次,那么使$[p-k,p+k]$满足条件的$k$是不超过$c$个区间(每加入一个新的$p$,都可能使本来不是众数的$p$再当一段时间的众数)。如果我们可以求出这些区间,就可以直接扫描线来回答所有询问了。啊你说怎么扫描线?不会扫描线还敢做lxl题/jy(
爆力做法显然就是枚举$k$维护众数,这样做是$O(n)$的。
要优化,先观察一些性质。每个区间的左端点处,一定是遇到了一个新的$p$;右端点则不一定,这个问题我们先不管。
考虑怎么做一些预处理来加速这个。我们可以尝试一次跳到下一个位置。预处理$f(i,j)$表示从$i$往右走最多多少步,可以保持每个数的出现次数都不超过$j$;$g(i,j)$是往左。这样我们可以很快地求出左端点,右端点也可以二分一次搞定,问题是预处理这两个东西复杂度难以接受。
根号分治。对于出现次数多的数,我们直接用第一个爆力;否则,我们用到的$f,g$第二维不会超过根号,可以用一个dp来预处理。总复杂度就是$O(n\sqrt{n}+q\log n)$。
分治结合分块
讲了这么两种套路 :
-
对分治剩下部分的大小根号分治。
-
$T(n)=2T(\frac{n}{2})+O(n\sqrt{n})$之类的递归式,这个东西的解是$O(n\sqrt{n})$。
ctsc2010 珠宝商
树,每个点有一个字符,还有一个串$t$,求所有有向路径上的字符串在$t$中出现次数之和。
先给$t$建一个sam,然后我们的爆力就可以枚举起点然后跑,复杂度$O(n^2)$。
考虑点分,问题是我们没法把两条路径接起来,不过这个是二路合并,所以可以考虑枚举一边算另一边这样的。考虑一条路径$u\rightsquigarrw c\rightsquigarrow v$,对于后一段可以直接在sam上跑,对于前一段我们
noi2020 时代的眼泪
矩形顺序对数。
把查询矩形在树套树上拆成$\log^2$个矩形,它是两维各$\log$个区间的笛卡尔积。矩形内的贡献可以直接算,两个不在同一行也不在同一列的矩形的贡献也是简单的,问题是在同一行或同一列的矩形,这里我们需要求一维的一个线段树区间和查询矩形的另一维的笛卡尔积的顺序对数。我们把这个查询挂到这一维的线段树上,然后用Yuno loves sqrt tech. I的分块做法。这个分块的复杂度是$O((n+q)\sqrt{n})$,线段树每一层总长度是$n$,有$O(q)$次查询,而$\sqrt{n}$每层衰减到$\frac{1}{\sqrt{2}}$,于是总复杂度是$O((n+q)\sqrt{n})$,树套树部分是poly log的。
cts2021 半平面修改查询