来到宇宙中心曹县所在的省份参加省队集训。
还有很多锅,可能很久才能补完,不过反正没人看,有人看大家也不要着急(
目前在补Day3,意思是12已经补完了/jy。
Day1
模拟赛
兔队(PinkRabbit)搬题。
T1 permutation
XXI Opencup, GP of Tokyo, Problem. I
CF Gym 102978I
给一个长\(m\),值域\([1,n]\)的串\(x\),计数有多少个长\(n\)的排列以这个串作为字典序最小的长\(m\)的子序列。\(n,m\leq 2.5\times 10^5\),膜\(998244353\)。
两个特殊性质部分分,分别是\(x\)单增和\(x_2=1\)。
先考虑第二个部分分。什么时候不能选\(x_1=1\)作为字典序最小的子序列?当\(1\)后面不足\(m-1\)个数的时候。而\(x_2=1\),这说明\(1\)一定在\(n-m+1\)这个位置上,而剩下的部分一定紧凑地排在后面。
所以,我们考虑\(x_1\)的位置,它可能在前面任何一个位置,进一步你发现前面是全排列。但是如果前面有比\(x_1\)小的,那么不可能取到\(x_1\),我们特判一下输出\(0\)。
然后考虑第一个部分分。考虑把不在这个子序列里面的数插入进去。打表你发现此时每个数可以插入的空位是一个前缀,并且随着数的增大这个前缀变长,具体怎么样可以自己观察。这样我们的决策就没有后效性了,所以我们直接从小到大乘起来就好了。
正解考虑把这两个结合起来。(然而我都打出来了,没想到正解)
考虑第一个\(x_i>x_{i+1}\)。此时一定是\(x_{i+1}\)因为后面的数太少了之前没法取,可以类似第二个部分分得到它和后面的数位置已经确定。此时前面的数就是第一档部分分了。复杂度\(O(n)\)。
T2 game
2020-2021 ACM-ICPC, Asia Nanjing Regional Contest, Problem. M
CF Gym 102992J
现在有一排石子堆,第\(i\)堆有\(a_i\)个。Alice和Bob要玩Nim游戏,Charlie提出了一些请求,每次让一个区间的石子堆对\(x\)取\(\max\),或者询问对于\([l,r]\)中的石子堆,并加入一堆有\(x\)个石子的石子堆之后,Alice和Bob谁会赢,如果Alice会赢第一步有多少走法。\(n,q\leq 2\times 10^5\)。
谁会赢就是维护区间\(\mathrm{xor}\)和,设为\(s\),然后看\(s\operatorname{xor}\)上\(x\)是不是\(0\)。
第一步合法的走法就是可以把\(\mathrm{xor}\)和变成\(0\)的走法。如果\(a_i\operatorname{xor}s<a_i\),那么第一步把\(a_i\)取成\(a_i\operatorname{xor}s\)即可。
发现\(a\operatorname{xor}b<a\)当且仅当\(b\)的最高位上\(a\)是\(1\),于是问题变成查询区间中某一位上是\(1\)的数的个数。
考虑吉老师线段树。做完了。复杂度\(O(n\log n\log v)\)。
当场写完!结果修改写错了(
T3 skate
XIX Open Cup, GP of Korea, Problem B
CF Gym 102059B
有一个\(n\times m\)的滑冰场,场上每个格子可能是空地或者障碍。
你的移动方式是,选择上下左右中的一个方向,然后向那个方向滑过去,直到到达边界或者撞到障碍才停下。
你从一个空地出发,需要经过一些标记点(滑过去也算经过)。问有没有可能经过所有标记点。\(n,m\leq 50\),\(5\)组数据。
考虑一个经典做法,我们对于每个位置,求出它所在的极长的横着和竖着的段。显然有如果你在一个极长段的任意一个位置停住了,你接下来都可以走遍这个段。同时,一个标记点被走到了,当且仅当它所在的横着的段和竖着的段至少一个被走到了。
你看到了一个2-SAT!
然后问题就是怎么在2-SAT上描述各种限制,从而充要地得到一条路径。
实际上只需要表示两个段不能互相到达,此时选了一个不能选另一个。为什么满足这个限制就等价于有解?
首先证明充分性,即满足这个限制一定有解。如果满足这个限制,说明我们选的任意两个段\(a,b\),要么\(a\)可以走到\(b\),要么反过来,要么可以互相走到。所以这是一个竞赛图加上一些重边,我们缩SCC之后还是有一样的结论——得到一条链,沿着链走就可以得到一条合法路径。
然后必要性显然,证完了。复杂度\(O((nm)^2)\)。
期望得分50+100+52=202,实际得分60+15+4=79。
挂分王!
讲课
图论咋提宣讲。
Jump
XVI Open Cup, Grand Prix of Asia
https://official.contest.yandex.ru/opencupXVI/contest/2145/problems/C/
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=010391
有一个数轴,数轴上有一堆点\(a_i\),有一堆询问,问你从\(s\)出发,每次选择一个\(a_i\)进行对称,最少几次到\(t\)。\(n\leq 200,v\leq 10^4,q\leq 10^5\)。
考虑对称出来式子的形态,是\(2(a_{p_k}-a_{p_{k-1}}+...+(-1)^{k+1}a_{p_1})+(-1)^ks\),移个项问题就变成求一堆\(a_i\)的交错和等于\(t-(-1)^ks\),并且项数尽量少。我们枚举\(k\)的奇偶性,然后就可以得到一个更简单的式子。
考虑拆点,每个点拆成正和负两个点,然后从\(0\)开始跑最短路,胡乱连边即可。复杂度\(O(v\log v+q)\)。
Today is a rainy day
ICPC 2015 Asia East - Beijing Regional
https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=5275
给定串\(s,t\),你可以对\(s\)进行若干次操作,每次是修改一位或者把一种字符完全替换成另一种,求把\(s\)变成\(t\)的最小操作数。字符只有123456,\(n\leq 100\)。
考虑替换操作一定可以放到最前面做,所以我们可以枚举一个映射,然后直接搞。映射只有\(6^6\)种,可以接受。
不过怎么才能找到最小操作数呢?考虑最多只有\(6\)次操作,先bfs一下预处理,复杂度就是\(O(6^6)\)的样子,不过它是多少都没问题。
Walk
收录于 优化建图。
树上传送
LYDSY Monthly Contest
https://www.lydsy.com/JudgeOnline/problem.php?id=5129
简单题。直接点分治优化建图。
Travel
http://acm.scu.edu.cn/soj/problem.action?id=4444
有一张完全图,其中\(m\)条边边权是\(a\),剩下的边权是\(b\),求\(1\)到\(n\)的最短路。\(n\leq 10^5,m\leq 5\times 10^5\)。
考虑\(1\leftrightarrow n\)的边权。如果是\(a\),那么答案已经至多是\(a\)了,要想更新答案我们不可能再走\(a\),此时是保留所有\(b\)边的一个bfs,或者说补图bfs。如果这个边权是\(b\)就很好说。
考虑因为是完全图,我们本来应该每个点都找一遍\(1,...,n\)来着。为了搞快点,如果一个点已经在队列中,我们希望找邻接点的时候跳过它。
每次扔进队列都是删除。删除、查找后继,可以使用并查集或者链表来实现。并查集复杂度\(O((n+m)\alpha(n))\),或者链表\(O(n+m)\)。
The Kirakira Cycle
Moscow International Workshop ACM ICPC 2016 Day 3, Division A: SJTU Dreadnought Contest
https://official.contest.yandex.ru/mipt2016autumn/contest/3163/enter/
给出\(n\),定义\(f(x)=\sum_{i=1}^nx\bmod{i}\)。对于\(i\geq 1\),我们连边\(i\rightarrow f(i)\)。求最大环长。\(n\leq 10^4\)。
\(f\)的值域显然是\([0,\frac{n(n-1)}{2}]\)。环上所有点只可能出现在这里面。
算一次\(f\)需要\(O(\sqrt{x})\)的复杂度,全算一遍无法承受。你问咋算?整除分块啊!
打表\(f\)你发现它非常混乱。混乱有什么好处?
随机!\(f\)出现在\(\frac{n(n-1)}{4}\)附近的概率很不低,那么我们猜测环上有一点在这附近的概率也不低。选一个点开始bfs即可。
加一个小数据爆力就可以过了。
这题也可以直接递推\(f\)得到一个更优秀做法。考虑\(f(x)-f(x-1)=n-\sum_{d\vert x}^nd\),这就很好,于是我们可以单点求值一次,然后快速求出\(\frac{n(n-1)}{4}\)附近一段的值(复杂度是\(O(len\log n)\)),因为这一段值很多,这样做可以加速一些。
新年的繁荣
UOJ Goodbye Yiwei
https://uoj.ac/problem/176
好题。收录于 sos-dp。咕咕咕。
病毒实验
JOI Open 2019
https://loj.ac/p/3155
好题。看懂了再写。咕咕咕。
Expectation
矩阵树定理+拉插裸题。
白金元首与独舞
CodePlus 2017 December Contest
https://loj.ac/p/6259
胡乱建图,内向树计数就是了。
生成树
三种颜色的边,求蓝绿边数分别不超过\(g,b\)的生成树个数,膜\(998244353\)。\(n\leq 40\)。
非常简单,直接拿生成函数扔进去,为了快速我们就拉插插出来。
怎么二元多项式拉插?
我现在只会网格状的……一般情况以后再说,一般用不到(
假设要用\(n^2\)个点插出二元\(n-1\)次多项式,其中每个点是\((x_i,y_j)\),\(x,y\)是两个长\(n\)的序列。这里\(n-1\)次说的是\(x,y\)的最高次都是\(n-1\)。
考虑与一元拉插完全相同的方法,我们构造一个函数\(l\)来拆开贡献。这个函数好像叫 插值基函数?
\[l_{i_0,j_0}(x,y)=\left(\prod_{i=1}^n\frac{(x-x_i)}{(x_{i_0}-x_i)}\right)\left(\prod_{j=1}^n\frac{(y-y_j)}{(y_{j_0}-y_j)}\right)\]容易发现这个函数满足\(l_{i_0,j_0}(x_{i_0},y_{j_0})=1\),而且对于其它\(i,j\)有\(l_{i_0,j_0}(x_i,y_j)=0\)。所以就插完了,答案多项式就是
\[\sum_{i=1}^n\sum_{j=1}^nf(x_i,y_j)l_{i,j}(x,y)\]。复杂度\(O(n^5)\)。
生成树计数
Beijing Team Training
https://www.luogu.com.cn/problem/P5296
无向完全图,求所有生成树边权和的\(k\)次方和。\(n,k\leq 30\),膜\(998244353\)。
经典题。
\(k\)次方,你想到了什么?
\(k=1\)的时候经典做法是用GF,所以我们还是用GF。
为了简单我们先考虑两条边。我们直接二项式定理爆力展开 :
\[(w_1+w_2)^k=\sum_{i=0}^k\binom{k}{i}w_1^iw_2^{k-i}\]不是很好拆。不过看到这样的组合数,要拆式子,你想到什么?
这是个二项卷积啊朋友们!
\[\frac{(w_1+w_2)^k}{k!}=\sum_{i=0}^k\frac{w_1^i}{1!}\frac{w_2^{k-i}}{(k-i)!}\]于是可以写出EGF,每条边的EGF就是\(e^{w_iz}\),求出\(nk+1\)个点值之后拉插即可。复杂度\(O(kn^4)\)。当然也可以爆力实现多项式运算做到\(O(k^2n^3)\)。
先扯两句BEST定理。
首先这个定理你要读bai si te我没啥意见,但是实际上它是四个发现者的名字缩写拼起来的。四个人分别是de Bruijn,van Aardenne-Ehrenfest,Cedric Austen Bardell Smith,W. T. Tutte。
它用来计数有向欧拉图的欧拉回路个数。对于一个起点\(s\),记\(T(s)\)表示以\(s\)为根的内向树个数,\(\mathrm{deg}(u)\)表示\(u\)的入度(或者出度,都可以),则这张图的欧拉回路数是
\[T(s)\prod_{u}\mathrm{deg}(u)!\]不过现在如何定义两条欧拉回路不同可能还有点问题。BEST定理认为重边也是不同的(如果我们希望重边相同,只需要除掉每个重数的阶乘),并且两条欧拉回路循环同构就认为它们相同(也可以认为是钦定了一个起点)。
注意只有是欧拉图的时候这个定理才有意义。
这个定理也可以推出在欧拉图中所有点分别为根得到的内向树数量相同。
无向图欧拉回路计数是不可做问题。
C4
AtCoder Grand Contest 051
https://atcoder.jp/contests/agc051/tasks/agc051_d
四个点的环,边无向,分别有重数\(a,b,c,d\)。求从\(1\)开始的欧拉回路数量,认为重边全部相同。\(a,b,c,d\leq 5\times 10^5\)。
BEST定理。
但是BEST定理只能做有向图?注意到重边数量很少,所以我们可以枚举\(1\rightarrow 2\)有多少条,那么因为需要是欧拉图立刻可以推出每两个点之间边的情况。然后BEST定理就好了。
注意这题认为重边都相同,所以除掉几个重边数量的阶乘就好了。复杂度懒得算,反正肯定能过/jy
Binary Code
ICPC 2016, Northeastern European Regional Contest(Northern Eurasia).
https://codeforces.com/gym/101190/problem/B
给一些01串,每个串有最多一个位置是?。你要给?填上0或1,使得没有一个串是另一个串的前缀。构造方案。\(\sum \vert s\vert\leq 5\times 10^5\)。
注意是 最多一个位置!
01变量,这种问题就可以考虑2-SAT。
把每个串的?分别取0/1塞进trie,然后取出每个串的结尾建立虚树,我们就知道如果取了一个点,那么到根链上所有点都不能取。所以要支持一个点向一个树上到根的链连边,树上前缀和即可。
Flags
AtCoder Regular Contest 069
https://atcoder.jp/contests/arc069/tasks/arc069_d
最小值最大,显然二分答案。
然后就变成,如果选了\(x\),那么\([x-mid+1,x+mid-1]\)全都不能选。2-SAT。
爆力线段树连边,可以做到\(O(n\log n\log v)\)。这就很拖拉机。
发现每次连边长度全都是一样的,所以可以给数轴按这个长度分块,那么每一次连边恰好都是一个块的前缀和一个块的后缀,可以每块一个前后缀和解决。值域1e9?把没有东西的块和没有东西的位置都忽略就好了。
这题也可以给点离散化,然后用滑动窗口优化建图,也就是连边的区间排序后\(l,r\)均单调递增之后的做法。
哦你说滑动窗口优化建图是什么?收录于 优化建图,例题就是这一道。
Hall定理说的是,一个二分图,左部点有完美匹配,当且仅当每个左部点子集邻接的右部点个数都至少是这个子集的大小。
为了方便,对于一个某一部点的子集\(A\),定义\(\Gamma(A)\)为\(A\)邻接的另一部点集合。
常用于在判断完美匹配存在性的题中推式子。要想直接求完美匹配难以用这个。
LYZ
16th Polish Olympiad in Informatics(POI2009)
https://szkopul.edu.pl/problemset/problem/kadKFW3YScAMW8o20u0BctQh/site/?key=statement
https://www.luogu.com.cn/problem/P3488
现在有\(1,...,n\)每个尺码的鞋子各\(k\)双。有一堆人要穿鞋子,脚长\(x\)的人可以穿尺码在\([x,x+d]\)的鞋子。支持修改一个脚长的人数,查询是否可以给所有人分配鞋子,使得每个人都能穿到鞋子。
二分图匹配,左边是每个人,右边是每个鞋子,每个人到一个区间的鞋子连边,原问题相当于问有没有完美匹配。
爆力Dinic显然没有前途。Hall定理。
考虑对于一个人的集合\(A\),\(\vert A\vert<\vert\Gamma(A)\vert\),那就是\(\vert A\vert-\vert\Gamma(A)\vert<0\)。所有集合都满足就很不好,我们转而找一个不满足的,也就是找一个\(\vert A\vert-\vert\Gamma(A)\vert\geq 0\)的,那自然可以变成最大化\(\vert A\vert-\vert\Gamma(A)\vert\)。
发现一个性质,如果选择两个人,那么他们连向的区间交越大,\(\vert\Gamma(A)\vert\)越小,所以我们希望选的人是一个区间。
然后就变成了选出一个人的区间,最大化它的点数减去它对面区间的点数。写出式子来看看?
\[\begin{aligned} &\sum_{i=l}^ra_i-(r-l+1+d)k\\ =&\sum_{i=l}^ra_i-(r-l+1)k-dk\\ =&\sum_{i=l}^r(a_i-k)-dk \end{aligned}\]于是变成了单点修改全局最大子段和,线段树即可。
Rooms
给一张地图,每个房间是极大同色四连通块,每次查一个矩形与多少房间有交。\(n,m\leq 2000,q\leq 5000\)。
复杂度是\(O(q(n+m))\)。
考虑每个连通块选一个关键点,然后先统计矩形内的关键点数量,可以使用二维前缀和。
考虑关键点不在矩形内的所有房间,它们一定跟这个矩形有交。所以我们爆力枚举矩形边上一圈的点,统计关键点在外面的部分。
Xor-matic Number of the Graph
图,边权,对于所有三元组\((u,v,w)\)满足\(u<v\),且\(u,v\)之间有一条边权异或和为\(w\)的路径,求\(w\)之和。\(n\leq 10^5,m\leq 2\times 10^5,w\leq 10^{18}\),膜1e9+7。
类似 最大xor路径。求出所有非树边确定的环,扔进线性基,然后问题变成对于随便一条边权异或和为\(w\)的路径\(u\rightsquigarrow v\)和能被线性基表出的\(x\),求\(w\operatorname{xor}x\)的和,因为我们得出的\(w\operatorname{xor}x\)一定互不相同。
这个\(w\)可以用一个\(d_u\operatorname{xor}d_v\)得到,其中\(d\)是dfs树上的前缀和。
众所周知可以表出的\(x\)有\(2^{\vert S\vert}\)种,\(\vert S\vert\)是线性基大小。
然后很自然地我们按位考虑。现在问题变成对于每一位求它有多少种方式得出来一个\(1\)。
考虑怎么搞。发现一件事情,就是对于每一位,所有可以表出的\(x\)们在这一位上要么全是\(0\),要么恰好一半是\(1\)。简单推论是,这个\(x\)不管再异或上什么都仍有这样的性质。
那么我们对于每个全是\(0\)的位,需要选这一位是\(0,1\)的\(d\)各一个;对于每个一半是\(1\)的位,不管怎么选都有一半的\(x\)跟选的\(d\)异或起来得到\(1\)。所以我们设\(c_0,c_1\)表示懂的都懂,这一位被计数的次数就是
\[c_0c_1+\binom{c_0+c_1}{2}\]然后乘上位权,乘上可以表出数的数量,全加起来就是答案了。
注意这题图可能不连通,需要对每个连通块分开计算。
Bajtocja
有\(d\)个点集相同的图,一开始都没有边,支持在某个图连一条边,或者查询有多少点在所有图中都连通。\(d\leq 2000,n\leq 5000,m\leq 10^6\)。
考虑每个图开一个并查集,两个点在所有图都连通相当于它们的集合代表元都相同。
给每个点在各图的代表元们进行hash。合并集合的时候,我们启发式地爆力改较小的集合里面的点,复杂度是\(O(dn\log n+m\alpha(dn))\)。用随便什么东西维护hash值,插入删除的同时更新答案即可。
Rally
POI2014
给一个DAG,可以删一个点,最小化最长路长度。
删一个点 这件事就很好。我们可以对于每个点预处理它为结尾和开头的最长路,两遍bfs就可以搞定,分别记为\(d_1,d_2\)。
拓扑排序之后,你发现另一个性质 : 一条路径的拓扑序是严格递增的。所以,如果一条路径包含某一条边,那么拓扑序在这条边两端点之间的点,都不可能包含在这条路径中,也就是说删掉这些点不会对这条路径造成影响,那么删掉这些点得到的最长路长度就需要对经过这条边的最长路取\(\max\)。
所以我们可以枚举每一条边,然后它相当于对一个拓扑序的区间取\(\max\),用你喜欢的数据结构维护即可。这里可以用扫描线+堆简单地做到\(O(n\log n)\)。
怎么证明充分性?好像不充分……还有点小问题,那就是删掉一个点之后,最长路可能只经过拓扑序小于它的点(或者反过来),也就是说这个最长路并没有跨过这个点,这种情况在上面并没考虑到。所以我们还需要对于每一个拓扑序前缀求出\(d_1\)的最大值,表示只在这个前缀里走的最长路,后缀类似。现在就完全没问题了。
Tournament cycle
求有多少个有标号竞赛图包含一个大小为\(k\)的环。\(n,k\leq 5000\),膜\(998244353\)。
结论 : 如果有一个大小为\(k\)的环,那么有所有大小为\(1,...,k\)的环。
我们反过来算,计算有多少个竞赛图没有大小为\(k\)的环。
相当于是说没有大小至少是\(k\)的SCC。
进行dp,设\(dp(i)\)表示\(i\)个点的答案,就可以枚举最后一个SCC的大小,用组合数选出来这个SCC进行转移。
然后问题变成这个SCC的方案数,也就是强连通竞赛图计数。这是著名问题,可以dp或者带项式预处理。
诶这个dp也可以带项式加速?不知道。
Day2
模拟赛
还是兔队搬题。
T1 segtree
zsy瞎写过了/xia
qlr随机过了/xia
suxxsfe随机55/xia
我输出随机数爆零/xia
原题CF1120D,有魔改。
给一棵树,一开始点权全是\(0\)。你可以进行若干次操作,每次选择一个点,给它的子树都加上一个数。每个点有一个代价\(v\),每次操作这个点需要支付对应的代价。求最小的代价,使得每个叶子的点权不同,构造方案。\(n\leq 2\times 10^5,v\leq 10^9\),你的操作数必须是\([1,10^9]\)的整数。
这题难点在于构造操作数。
只是求出要操作什么东西的话,非常简单!我们先假设每次操作都可以随便选,那么两个叶子到根的链上,被操作的集合不同,它们的值一定可以不同。
然后你就发现,我们从每个叶子都选了开始贪心,每个点可以选一下来换子树里一个点不选。可以用线段树或者可并堆维护贪心,也可以神秘树形dp。
然后至于怎么构造?直接随机是不行的,因为有生日悖论,\(2\times 10^5\)得把值域开到\(10^{12}\)甚至更多才能稳过。
但是qlr太神了!他写的有冲突就重新随,据说实践中大约30次就可以得到一组对的。这好像很靠谱。
考虑一个简单结论,每个叶子到根路径上最深的被操作的点一定是不同的,证明显然。
所以这个形成了一个一一对应关系,我们可以利用这件事来操纵每个叶子的权值。
找到被操作点和叶子的对应关系,然后自顶向下进行调整。兔队的做法是钦定每个叶子的值和它的编号膜\(n\)同余,每次操作都把当前点对应的叶子的权值搞对。
复杂度\(O(n)\)。
T2 strhash
终于不挂分了 qwq
另外为什么都是T2最简单啊(
给一个随机字符串,求它所有子串中hash值最大的。基数\(2333333\),模数\(998244353\)。多组数据,\(T\leq 50,\sum \vert s\vert\leq 2\times 10^6\)。
考虑因为是随机,子串的hash值应该近似于均匀分布,所以从上到下枚举应该期望\(O(\frac{p}{n^2})\)次就可以找到答案。
然后就是怎么判断枚举的答案\(k\)是否可行。考虑推式子
\[\begin{aligned} pre_{r}-base^{r-l+1}pre_{l-1}&=k\\ base^{-r}(pre_{r}-k)&=base^{-l+1}pre_{l-1} \end{aligned}\]。然后我们就可以枚举一个右端点,用hash table支持查询左端点,如果这个值最小的左端点在枚举的右端点左边那就可行。复杂度\(O(\frac{p}{n^2}n)=O(\frac{p}{n})\)。我忘了预处理幂,多个\(\log\),但是手写了hash table,跑的飞快(
当\(n\)很小时,可以爆力\(O(n^2)\)。稳得很。
结果因为这题直接小数据爆力,大数据998244352,就可以得到85pts,我被神们吊起来打。
诶这个复杂度应该是\(O(\sqrt{p}+n)\)。
T3 multbfs
原题CF1086F。
3 5 0 0
有一个平面,你要在整点上做多源bfs。一开始有一些bfs的起点,它们的\(dis\)为\(1\);每次会扩展到切比雪夫距离为\(1\)的点。对所有\(dis\)不超过\(k\)的点的\(dis\)求和。\(n\leq 50,1\leq k\leq 10^8,-10^8\leq x,y\leq 10^8\),膜\(998244353\)。
把\(dis\)看成时间来考虑。
发现每一时刻,被遍历到的点会扩大一圈,而答案会增加(这一时刻的面积减去上一时刻的面积)乘上这一时刻。
这是一个分段函数,有\(O(n^2)\)个时刻会有一些块撞在一起(枚举两个起点,它们切比雪夫距离+1的一半上取整就是相交时间),而每一段内部当然是一个三次函数,可以拉插插出来。
然后怎么单点求值?既然是两个矩形并面积的差,我们可以用扫描线。
不过并没有必要开线段树!离散化之后瞎写就可以了,复杂度\(O(n^4)\)。
唐椰叶给出了一个\(O(n^2)\)做法。
先切比雪夫转曼哈顿,然后从每个点画横线竖线,会把平面切成\(O(n^2)\)个矩形。为了方便处理,我们在最外圈再加上一个巨大的框,并使得这个框外不会被走到。
然后你就发现,每个矩形应该是四个角先被走到,然后从四个角出发扩展到矩形里面的所有(会被走到的)点。所以先求出每个角被搜到的时间。
考虑每两个角所扩展的部分,如果相交,一定有一条分界线,使得两边分别是两个角的贡献。对于邻角是一条横线或者竖线,对角则是一条45度的斜线。这条线可以很容易地算出来,还是距离除以\(2\)就好了。
所以考虑每个角的贡献。
发现它是一个(可能退化的)五边形,比如左下角看起来是这样的
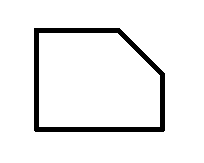
,其中下面和左面的线是矩形边框,上面和右面是和左上角、右下角的分界线,右上是和右上角的分界线。然后我们硬计算它的贡献即可。咋算?不知道/cy反正唐椰叶算出来了。
唐椰叶 : 写一句就得想十分钟
期望得分24+100+12=136,实际得分0+100+12=112。至少不是挂分王了。
讲课
数据结构!
Sinao
有一排草,一开始高度全是\(0\),每天每棵草会长高\(a_i\)。在若干个\(d_i\)天,兔会吃掉所有高度超过\(b_i\)的草,求每次吃了多少草。\(n,q\leq 10^5\)。
按\(a_i\)排序,每次吃掉的就是一个后缀。线段树维护这个长高的操作,然后二分出吃掉的后缀,再支持推平操作即可。
动态图
离线动态图连通性。
cdq分治。
二分图
懂的都懂!
线段树分治。
直径
树,每次给两个区间,查各选一个点距离的最大值。\(n,q\leq 10^5\)。
直接合并两个集合的直径。使用线段树,\(O(n+m\log n)\)。
用st表,然后建立虚树做四毛子,\(O(n+m)\)。
但是你发现并不能四毛子!因为编号信息量太大。带\(\log\)就带\(\log\)吧。
Painting Edges
线段树分治!
先假设所有操作都被执行了。
不挂操作,而是每次遇到一个操作,看它会不会被执行,如果不会被执行就把之前的颜色拿过来代替它的颜色。实现的时候可以在时间线段树上插入操作编号,而去修改全局的操作信息数组。
Segment
懂的都懂!
李超树。
兔讲了一个基于二进制分组的好玩的做法。
这里扯一句无关的名言 : 二进制分组是分治的不完全执行。
EI的集训队论文,除了烤兔兔还有一个东西,说的是这个问题之类的问题中函数\(\min/\max\)的段数。这里是线段,段数是\(2n\alpha(n)+O(n)\)。
用神秘做法给每组求一个\(\max\),这个函数段数是\(O(n\alpha(n))\),合并的时候直接归并或者重构,总复杂度就是\(O(n\log n\alpha(n)+m\log^2 n)\)。据说可以用分散层叠优化掉查询的一个\(\log\),反正我不会。
楼房重建
我之前写了啥来着……
Election
A和B竞选总统。有一排选民,每个人支持A或B,或者中立。
你要把选民分成若干长度在\([l,r]\)之间区间的并,每个区间会有一票,这一票将投给区间中支持人数更多的候选人。如果两方支持人数一样多那就弃票。
现在你可以随便划分选民,最大化A的得票减去B的得票。\(n\leq 10^6\)。
把A看成\(+1\),B看成\(-1\),中立看成\(0\)。设\(t(x)=[x>0]-[x<0]\)表示一个区间的权值。
\(n^2\) dp很简单,设\(dp(i)\)表示懂的都懂,有
\[dp(i)=\min_{j=i-r}^{i-l}dp(j)+t(pre_i-pre_j)\](上下界不知道是不是错了,不过不重要)发现这个后面的东西只和\(pre_i\)与\(pre_j\)的大小有关。这启示我们把\(pre\)扔进状态。
对每个\(pre\)开一个vector,然后这个转移可以用单调队列优化。需要支持在某个单调队列里面插入、删除,查询所有单调队列队首的最大值。
用线段树维护所有队首,做完了。复杂度\(O(n\log n)\)。
文明城市
树,点权,支持修改点权,查询点权和最大的连通块的点权和。\(n,q\leq 10^5\)。
树上ddp。
线段树
有一个序列和一个长\(m\)的操作序列,每个操作是把一个区间推平成这个区间的最大值。
支持对序列的单点修改,以及对执行完一个区间的操作得到的序列做单点查询。\(n,m,q\leq 10^5\)。
考虑倒过来。倒着做,你会发现这个操作相当于合并连续段。咕咕咕。
树上的路径
给一棵树,正边权,求\(\mathrm{dis}(u,v)\)从小到大排序之后前\(m\)个值。\(n\leq 5\times 10^4,m\leq 3\times 10^5\)。
二分答案,然后爆力点分治!然后你发现这是仨\(\log\),T飞了。不过其实只需要先排好序,此后每次统计都是一个\(\log\)的,复杂度就是\(O(n\log n\log m)\)。
另一个做法是,点分治,然后直接转成\(O(n\log n)\)个元素的超级钢琴做。
超级钢琴
序列,求出所有长度在\([l,r]\)中区间的和拿出来排序之后,前\(k\)个的和。\(n,k\leq 5\times 10^5\)。
先前缀和,问题变成对于\(s_i\),把\(j\in[i-r,i-l]\)的\(s_i-s_j\)都拿出来参与排序。
考虑开一堆堆来维护这个东西。怎么每次把一整个区间push进去?
这个实际上很简单!我们记录一个三元组\((i,l,r)\)表示上面那个东西即可。然后它里面的最大值就可以用st表\(O(1)\)查出来。
怎么实现弹掉最大值?我们发现最大值如果是\(j\),那么去掉\(j\)这个东西分成两部分,分别是\((i,l,j-1),(i,j+1,r)\),扔回去即可。
等差数列
单点修改,查询区间重排能不能变成公差为\(k\)的等差数列。强制在线。
经典题。
兔队给了一个更棒的做法,说的是能构成等差数列,等价于满足以下三个条件 :
-
最大值减最小值等于\(k(r-l)\)
-
数不重复
-
差分数组的\(\gcd\)是\(k\)
,看起来很容易证明。线段树维护最大值、最小值,\(pre\)的\(\max\)以及差分的\(\gcd\)即可。
注意维护\(\gcd\)的线段树是一个\(\log\)的!复杂度\(O((n+q)(\log n+\log v))\)。
Good Subsegments
给一个排列,每次查一个区间,问有多少子区间构成值域连续段。\(n,q\leq 1.2\times 10^5\)。
简单做法 : 回滚莫队,套一个CF526F的线段树。\(O(n\sqrt{n}\log n)\)。
普通做法 : 再次考虑526F的线段树。
每次右端点右移,影响一个时间后缀。所以每个左端点的查询相当于一个历史最小值和个数的查询。使用吉老师线段树即可。
神仙做法 : 析合树。
Puzzled Elena
有根树,点权,对于每个点,求出子树里有多少点点权和它互质。\(n,a_i\leq 10^5\)。
先莫反!变成对于因数们做一些事情。
子树可以变成区间,然后拆成前缀和相减,然后扫描线扫过去。用一个桶维护,每次插入一个数就把因数们的什么东西扔进桶,查询就查所有因数,复杂度\(O(nd(n))\)。
Odwiedziny
树,点权,每次查询从\(u\)出发跳到\(v\),每一步跳\(k\)条边,求经过的点权之和。\(n,q\leq 10^5\)。
根号分治。对于超过根号的直接跳,少于根号的预处理\(u\)跳到\(1\)和\(1\)跳到\(u\)的答案,然后拆\(\mathrm{lca}\)即可。\(O((n+q)\sqrt{n})\)。
Bear and Chemistry
无向图,每次查询加入一些边之后,一个点集是否边双连通。询问互不影响。\(n,m,q\leq 3\times 10^5\),加入的总边数、点数均不超过\(3\times 10^5\)。
边双树。建立虚树然后连上新的边,再求一遍边双即可。奇妙?
Duff is Mad
类似于547E,我们建立ACAM。
然后问题变成,对区间每个串的终止结点子树\(+1\),求查询串所有点的和。
先对询问进行差分。
根号分治。认为各种东西都同阶。
对于长串,预处理这个前缀和。串个数是\(O(\sqrt{n})\),每次复杂度是\(O(n)\),乘起来是\(O(n\sqrt{n})\)。
对于短串,先离线下来。枚举前缀进行子树\(+1\)操作,扫到查询就爆力查。
注意到单点查询的总个数是\(O(n\sqrt{n})\),但是子树\(+1\)只有\(O(n)\)次,所以可以用根号平衡干掉BiT的\(\log\)。总复杂度\(O(n\sqrt{n})\)。
A Text Problem
有一个串\(t\),每次查询一个\(s\),求\(s\)在\(t\)中允许一个位置不同的匹配次数。\(\sum\vert s\vert,\vert t\vert\leq 10^5\)可以强制在线。
考虑建立\(t\)的前缀树和后缀树,然后枚举\(s\)那个不同的位置,分别求出此时\(s\)的前缀/后缀对应的\(t\)的前缀/后缀树上的结点。然后相当于求同时在两个子树中的所有\(pos\)个数,发现子树是区间,于是变成二维数点,主席树即可支持在线。
Matches Are Not a Child’s Play
3 4 0 0
树,点权,定义它的删除序列为 : 每次删除权值最小的叶子,把这些叶子的编号按删除顺序排列。
支持修改一个点的点权为比当前最大值更大的值,或者查询一个点在删除序列中的位置。
考虑每次操作之后,相当于把操作点和原来最大值的链全都移到删除序列的末尾。
考虑LCT维护连续段,然后同时用平衡树维护序列。做完了。
具体怎么做完了?我也不知道,反正兔做完了(
Day3
模拟赛
猫昕(nealchen)的题。
T1 city
给一个字符串,串只有abc三个字符。定义一个串的美丽度是它的长度的平方除以最小循环节的长度,求这个串所有子序列美丽度的最大值。\(n\leq 10^5\),\(10\)组数据。
考虑所有字符中出现次数最多的,它至少出现了\(\lceil\frac{n}{3}\rceil\)次,贡献是\(\lceil\frac{n}{3}\rceil^2\)。
考虑随便一个子序列,假设它的循环节长度是\(m\),一共循环了\(k\)次,那么这个串的答案是\(k^2m\)。
显然它最多的字符在每一个循环节至少出现\(\frac{m}{3}\)次,我们把这个单独取出来,它的最小循环节长度是\(1\),所以得到的答案是\(\left(k\lceil\frac{m}{3}\rceil\right)^2\)。
这就非常好,我们把这两个式子搞一下,得到要想用一个循环节不是\(1\)的串更新答案,必有\(\lceil\frac{m}{3}\rceil^2<m\)。
你发现只有\(m=1,2,3,5,6\)才满足这个限制,所以我们先爆搜出来。
然后非平凡循环串一定没有用,所以我们可以跑一遍kmp筛去循环串。这样只剩下\(99\)个串,硬跑就可以过了。
可以四毛子除一个$3$之类的。并且循环同构的串可以一起跑。
T1.5 field
经典网络流题,因为太广为人知被换掉了。
T2 qaq
有\(n\)个盒子,每个盒子里面有一些带编号的球,一开始第\(i\)个盒子里有且仅有\(a_i\)个编号是\(i\)的球。
接下来你可以按顺序进行\(m\)次操作,每次操作你会拿到两个盒子编号\(x,y\),你可以选择从这两个盒子里面各拿出一个球交换,或者不做任何操作。
最大化最后盒子\(1\)中不同编号球的数量。\(n,m\leq 3000\),\(10\)组数据。
还是经典网络流题。
考虑实际上只有最后到了\(1\)的球才有用,并且相同编号的球只有一个有用,我们不妨把问题修改一下,每个盒子里只有一个球,别的都是纸片。
这样就可以考虑球的交换,它可以抽象成流。
我们建立\(m\)层图,一开始给每个盒子分一个球,然后每次交换就是两个盒子之间连两条边。注意这里可以不拆点。每个盒子向下一层的盒子连它的大小,表示不能有多的球换过来。
然后你发现实际上每层只有一次交换,所以我们可以去掉所有没换的,实现中直接让每个时刻连向下一次被操作的时刻即可。
常数可能影响得分!猫表示写Dinic可以从\(t\)出发反着bfs分层,这样可以筛去很多不能到达\(t\)的点。注意\(s\)不能到达的点根本不会被dfs搜到,所以不影响效率。或者你写HLPP那肯定稳了啊(
复杂度\(O(\mathrm{maxflow}(n+m,n+m))\)。
T3 world
有\(m\)件物品要全分给A和B,两个人的物品栏各有\(n\)个格子,第\(i\)件物品只能放在A的\(x_i\)格子或者B的\(y_i\)格子,并且如果分给A会把A的得分增加\(a_i\),给B则会把B的得分增加\(b_i\)。最小化两个人的得分乘积。\(n\leq 5\times 10^5,m\leq 2n,a_i,b_i,\leq 10^6,\sum a_i,\sum b_i\leq 2\times 10^9\)。
每个物品栏的格子建一个点,把物品抽象成\((A_{a_i},B_{b_i})\)的边,现在我们要定向,指向哪个格子就是分给哪个格子。你发现每个点只有一条入边,所以形成了一个外向基环树森林。等等,也有可能是树,因为有的格子可能没有放东西。
考虑把两个人的得分看成平面上的坐标,那么我们要最小化乘积就是拿\(xy=k\)去切,所以我们知道答案一定在下凸壳上。对于基环树我们搞出两种定向的得分,对于树直接就是一个点,然后依次合并它们——这是闵可夫斯基和,最后直接枚举下凸壳上的点得到答案即可。复杂度瓶颈是闵可夫斯基和的\(O(n\log n)\)排序。
好妙啊!
期望得分40+0+0=40,实际得分0+0+0=0。/kk
讲课
概率期望!
猫毒瘤!
AGC028B Removing Blocks
考虑把和转成期望!
考虑一个线段贡献了多少次。这是快排啊!
考虑一棵划分的树。如果\(i\)被干翻的时候\(j\)产生了贡献(不妨先讨论\(i<j\)),说明\(i\)被干翻的时候\([i+1,j]\)都还没被干翻,也就是\([i,j]\)中\(i\)第一个被干翻。因为干翻时间是均匀随机的排列,这个概率应该是\(\frac{1}{j-i+1}\)。对所有\(i,j\)求和就得到答案。注意这是\(i<j\)的部分,\(i>j\)要反过来,不过其实好像乘\(2\)就可以了。注意这是期望,还要乘上情况数也就是\(n!\)才是答案。
CF605E Intergalaxy Trips
当然设\(E_u\)表示\(u\)走到\(n\)的期望。
考虑即使在期望意义下,最短路的贪心还是成立的,也就是说我们会尽量走到一个\(E\)更小的邻接点。所以我们得到一个式子
\[E_u=\frac{1}{1-\prod_{v}(1-p_{u,v})}\sum_{u\rightarrow v}p_{u,v}E_v\prod_{E_w<E_v}(1-p_{u,w})\]这个式子前面那个\(\prod\)说的是至少一条边开放,也就是能走出去的概率;后面那个\(\prod\)说的是比\(v\)更优的邻接点都走不动的概率。
所以有一个想法,我们按照\(E\)从小到大处理,这样就可以保证处理到一个点的时候,它的转移就是它周围所有处理过的点(,而不会出现没处理过的点)。注意到没有负权边,所以这个不就是Dij吗!
首先\(E\)最小的肯定是\(n\),我们把它扔进一个堆,每次取出堆顶在反图上进行更新。胡乱维护就好了。
CTS2019 随机立方体
进行二项式反演,把 恰好 变成 钦定。
考虑钦定出一个格子序列(而不是一个格子集合),方案数是\(n^\underline{k}m^\underline{k}l^\underline{k}\)。然后我们钦定这个序列的值从小到大,并且我们从左到右考虑把每个格子放进去可行的概率,总概率就是它们乘起来。
格子\(i\)填的数需要比所有和它有至少一维坐标相同的格子大,还要比之前那\(i-1\)个选的格子大,所以它要比所有和前\(i\)个格子有至少一维坐标相同的格子大。这样的格子一共有\(nml-(n-i)(m-i)(l-i)\)个(有\(n-i\)个横坐标没有选,另两维类似),那么这个概率就是\(\frac{1}{nml-(n-i)(m-i)(l-i)}\)。所以总概率就是\(\prod_{i=1}^k\frac{1}{nml-(n-i)(m-i)(l-i)}\)。
所以答案就是
\[\sum_{i=k}^{\min(n,m,l)}(-1)^{i-k}\binom(i,k)n^\underline{i}m^\underline{i}l^\underline{i}\prod_{j=1}^i\frac{1}{nml-(n-j)(m-j)(l-j)}\]。离线求逆元就线性了。
FJOI2019 新家具设计方案
给一个\(k\)维空间中的点集\(S\),每次询问一个子集\(T\),求有多少点满足各维都是非负整数、和不超过\(s\),并且左下角的\(S\)中的点恰好是\(T\)。\(\vert S\vert\leq 20,s\leq 10^5,q\leq 10^5\),各维都不超过\(10^5\),不取膜/jy
爆搜,考虑把恰好换成至少,这个可以求出当前子集的各维最大值,然后组合数选出来。
然后你发现我们算出来的其实是一个子集前缀和,可以逆法嘛塔一下搞回去。做完了。
CF963E Circles of Waiting
直接高消没有前途。主元法。
考虑拿从上往下看到的所有点的期望当做主元,然后如果我们知道了一个点左边,右边,上边点的期望,就可以得到这个点的期望,于是可以递推得到圆下面所有点用主元表示的期望。它们的期望应该是\(0\),于是得到\(2r\)个方程,解即可。复杂度\(O(r^3)\)。
uoj442 集训队作业2018 小Z的礼物
收录于 dp优化容斥。
表达式求值
给一个表达式,只有加减乘和括号还有一些未知数(用\(\_\)表示),现在给每个未知数随机填入\([1,n]\)中的不同整数,求式子的期望膜1e9+7。\(\vert S\vert\leq 5\times 10^4,n\leq 10^9\)。
乘法没有线性性。
注意到比如\((\_+\_)\times (\_+\_)\)这样的式子,拆开括号,它就是\(\_\times \_+\_\times \_+\_\times \_+\_\times \_=4\_^2\)!为什么?因为每个未知数是完全平等的。这也是我们之所以用\(\_\)而不是\(x,y,z\)表示未知数。
这就很好。这说明最后我们得到一个多项式,每一项都是\(a_k\_^k\),次数是最多乘号个数次,我们爆力模拟求出它的各项系数,然后就可以利用线性性拆开各项的贡献。
设\(g(m)\)是所有 选\(m\)个\([1,n]\)之间无序且互不相同的数乘积 的和。那么答案就是
\[\sum_m \frac{a_mg(m)}{\binom{n}{m}}\]接下来问题就是求出这个\(g(m)\)了。考虑加一维,变成\(g(n,m)\),然后从大到小选,容易写出递推式 :
\[g(m,n)=\sum_{i=1}^{n}ig(m-1,i-1)\]如果your math is toooooooooooooooooo strong,你可以看出来这**就是一个第一类斯特林数,可以\(O(m\log m)\)法法塔,但是这题模数不怎么好……也可以\(O(m^2)\)递推。
否则,你可以猜它是关于\(n\)的\(m\)次多项式,按上面的式子爆力递推,前缀和优化到\(O(m^2)\),然后\(O(m^2)\)拉插插一插即可。
AGC013E Placing Squares
咕咕咕。
进行dp,设\(f_i\)表示强制在\(i\)这里分的所有方案的权值和,可以写出转移
\[f_i=[i\notin X]\sum_{j\notin X}(i-j)^2f_j\]这个dp看起来很难优化。不过也可以!
首先我们假设\(i\notin X\),因为\(i\in X\)的点很少,可以拿出来爆力转移。
考虑当\(i\)右移一位的时候,我们爆力展开这个式子,并搞几个辅助数列来递推 :
\[\begin{aligned} f_{i+1}&=\sum_{j=0}^i(i+1-j)^2f_{j}\\ &=f_i+\sum_{j=0}^{i-1}(i-j)^2f_j+2\sum_{j=0}^{i-1}(i-j)f_j+\sum_{j=0}^{i-1}f_j\\ &=2f_i+2g_i+h_i\\ g_{i+1}&=\sum_{j=0}^i(i+1-j)f_{j}\\ &=f_i+\sum_{j=0}^{i-1}(i-j)f_{j}+\sum_{j=0}^{i-1}f_{j}\\ &=f_i+g_i+h_i\\ h_{i+1}&=\sum_{j=0}^if_{j}=f_i+h_{i} \end{aligned}\]所以可以写出转移矩阵进行矩阵快速幂 :
\[\begin{bmatrix} 2&2&1\\ 1&1&1\\ 1&0&1 \end{bmatrix} \begin{bmatrix} f_i\\ g_i\\ h_i \end{bmatrix} = \begin{bmatrix} f_{i+1}\\ g_{i+1}\\ h_{i+1} \end{bmatrix}\]呃这是\(i\notin X\)的转移矩阵,如果\(i\in X\),转移矩阵是这样的 :
\[\begin{bmatrix} 1&2&1\\ 0&1&1\\ 0&0&1 \end{bmatrix} \begin{bmatrix} f_i\\ g_i\\ h_i \end{bmatrix} = \begin{bmatrix} f_{i+1}\\ g_{i+1}\\ h_{i+1} \end{bmatrix}\]具体推法就是把之前推导中的\(f_i\)全换成\(0\)。
兔和猫的做法都是考虑组合意义,组合意义天地灭!
CF917D Stranger Trees 加强版
\(n\leq 5000\)。
原题\(n\leq 100\),可以矩阵树定理+拉插干翻它!但是\(5000\)并不能这么做。
先二项式反演掉\(k\),问题转化成钦定\(k\)条边重合、剩下随意的方案数,然后就可以缩起连通块,用Prufer定理来生成树计数。
然后我们得到方案数是
\[n^{n-k-2}\prod s_i\],其中\(s\)是每个连通块的大小。
然后问题变成,求所有钦定\(k\)条边的方案中,各连通块大小积的和。
可以树形dp!然而并不好做,并且复杂度高上天了。
考虑组合意义,是在每个连通块选一个点的方案数。(打 脸,实在是没有看到直接代数推导的做法)
我们设\(dp(u,i,j,0/1)\)表示 \(u\)子树内选了\(i\)条边和\(j\)个点,根节点所在的连通块没有/有选点 的方案数,复杂度是树卷积的复杂度\(O(n^2)\)。
顺子
对于一个序列,它是顺子当且仅当它相邻两项差的绝对值都是\(1\)。
求长度为\(n\),且所有是顺子的区间长度都不超过\(m\)的排列个数。\(m\leq n\leq 5000\),膜1e9+7。
长度都不超过\(m\),等价于没有长度是\(m+1\)的。
考虑容斥,我们钦定一些长度是\(m+1\)的顺子。假设钦定\(k\)个顺子的方案数是\(g(k)\),那么答案就是\(\sum_{i=0}^\)
如果两个顺子有交,它们一定同增或同减,所以我们可以合并它们。假设合并完了有\(x\)个区间,不在区间里的有\(y\)个数,那么方案数是什么?
考虑每个顺子可以由增减性和首项唯一确定,有\(2^x\)种分配增减性的方案,之后有\((x+y)!\)种分配数之间相对大小的方案,所以总方案数是\(2^x(x+y)!\)。
AGC024E Sequence Growing Hard
考虑如果我们第\(i\)次把\(v_i\)放到位置\(p_i\)前面,那就需要\(v_i>A_{i-1,p_i}\)。
考虑按加入时间排序,那么
咕咕咕。
CF506E Kitayuta’s Gift
咕咕咕。
loj Beta Round #7 匹配字符串
考虑dp,有\(f(i)=2f(i-1)-f(i-m-1)\),那个减就是考虑选\(1\)不行的情况。
现在显然可以爆力多项式取膜了!做完了。
另一种做法是转成DAG上带权路径计数问题,咕咕咕。
FJOI2020 凸多边形正则划分问题
求把一个\((k-2)n+2\)边形划分成\(n\)个凸\(k\)边形的方案数。多组数据,\(3\leq k\leq 200,n\leq 555555,\sum n\leq 10^8\),1s 1GB,膜1e9+7。
直接拉格朗EI反演。
组合做法 : 对偶图,变成求\(n\)个点的无标号无根\(k\)叉树计数,并且儿子有序。咕咕咕。
Day4
模拟赛
兔良心!
T1 degree
兔 : 大家开动脑筋乱搞就好了
给一张无向连通图,没有自环但是可能有重边,求一种定向方案,使得每个点\(u\)满足两个限制 : 入度至少是\(x_u\),出度至少是\(y_u\),构造方案,不存在输出-1。\(n,m\leq 5\times 10^5\),注意\(x_i,y_i\leq 1\)。
三种做法 : 上下界网络流,玄学,缩点。
suxxsfe和zsy写了上下界网络流。不必多说。
sqy和dwt写了玄学。
考虑干翻所有度为\(1\)的点。干翻之后剩下一个有欧拉回路的图,所以可以随便求一个欧拉回路分解。
问题出在可能有度为\(1\)的点没有限制,此时就需要胡乱处理它的边。
我和峰写了缩点。
先缩e-DCC,每个e-DCC可以按照dfs时的方向定向成SCC,而SCC中每个点只有一条入边一条出边。
接下来在树上乱搞即可。
He_Ren直接dfs树!给非树边打标记,然后做树的即可。
T2 digits
原题CF778E。
给一堆数\(b_i\)和一个怪数\(a\),\(a\)里面有一些?,你可以在?上填数。给出\(0,...,9\)的权值\(c_0,...,c_9\),定义\(f(x)\)表示\(x\)各位权值之和,你需要把\(a\)填完,使得它前面没有前导0,并且\(\sum f(b_i+a)\)最大。\(n\leq 1000,a,b_i\)位数都不超过\(1000,c_i\leq 1000\)。45pts是\(n\leq 8\)。
考虑数位dp,设\(dp(i,S)\)表示处理完了前\(i-1\)位,当前位有\(S\)中的数进位了的最大权值。转移显然。复杂度\(O(10len\cdot 2^nn)\)。
考虑一件很有意思的事情,对于每一位,如果不考虑上一位的进位,这一位只有最多\(\min(n+1,10)\)种进位情况。因为我们按这一位从大到小排序之后,每次进位的一定是一个前缀。
实际上,即使考虑上一位的进位,这一位也最多只有\(n+1\)种进位情况。假设处理到\(i\)位,按照前\(i\)位字典序从大到小排序,不管\(i-1\)位如何进位,由于\(i\)位的位权超过\(i-1\)位,并且\(i\)位上进位进出来的\(x\)一定不如原来就在\(i\)位上的\(x\)大,前\(i\)位的字典序不会改变。
我们可以用基数排序预处理排序的结果,排序不是复杂度瓶颈,那么接下来问题就是怎么优化转移。
诶你发现这个转移性质也比较优秀,因为每次进位的是一个前缀,我们可以很容易地\(O(n)\)递推转移需要的值。复杂度\(O(n\cdot len)\)。
T3 jump
有一棵树,有一个棋子在\(1\)号点,现在Alice和Bob两个人玩游戏,Alice先手,每个人每一次要把棋子移动到另一个点去,要求这一步移动距离必须大于上一步。Charlie现在要砍去一些子树,问对于所有不同的砍子树的情况,有多少种是Bob后手必胜。\(n\leq 2\times 10^5\),膜\(998244353\)。
考虑一个简单结论,两个人都不会走到任何一个直径端点,因为走直径就可以逼得对方无路可走。
所以我们可以标记直径端点为不可达。那么接下来重新求出直径,又会多出来新的不可达点……最后可以想象只有center留了下来。只有这个center就是起点\(1\)的时候,也就是Alice随便走都会炸掉的时候,Bob才能赢,所以问题变成计数有多少删子树的方案会留下\(1\)作为center。
考虑\(1\)是center的话,一定会有两条路径连出去构成直径。
dp,设\(dp(u,i,j)\)表示\(u\)子树内,只考虑重儿子和前\(j\)个轻儿子,砍到最大深度为\(i\)的方案数(相对深度),\(dp(u,i)\)则是考虑所有儿子。考虑前面选的深度\(x\)和第\(j\)个轻儿子\(v\)选的深度\(y\),可以写出方程
\[dp(u,\max(x,y),j)=\sum_x\sum_y dp(u,\max(x,y),j-1)+dp(u,x,j-1)dp(v,y)\]当然初始化\(dp(u,0,0)\)为重儿子的\(dp\) shift一位。
直接转移复杂度是树卷积的\(O(n^2)\),可以获得72pts!
你发现这是一个\(\max\)卷积,可以用前缀和-差分优化,不过这对复杂度并没有帮助……
不过接下来可以用长链剖分优化,式子什么的等我学了长剖再推。线性做法非常毒瘤,建一棵线段树维护转移会简单不少。
最后我们在\(1\)处进行合并即可。
好了我们回来推一推吧。考虑\(\max\)卷积是什么,呃就是先做前缀和,然后点积起来,然后差分掉。
所以我们要做的事情就是 :
-
点积上一个儿子
-
shift一位
注意要点积的长度实际上是总长度,因为这个前缀和会自动补全到重儿子的长度。这就很难受!
当然直接爆力线段树维护就可以一个\(\log\)。
要想做到线性,我们需要对后面的部分打标记。合并轻儿子的时候爆力重构轻儿子的\(dp\)就好了。实现起来还是挺麻烦的,毕竟长剖本身就挺容易搞错。
期望得分100+45+8=153,实际得分100+45+16=161。完全没挂!
讲课
CF咋提宣讲。
几乎全是黑色,快点水经验啊/jy
CF724E Goods transportation
显然最大流。建图是\(s\stackrel{p_i}{\longrightarrow}i,i\stackrel{c}{\longrightarrow}j,i\stackrel{s_i}{\longrightarrow}t\)。
然而这个跑不了1e4。(啊?CF不是2s 1e12吗?)
考虑dp。要dp最大流太**困难了,我们转成最小割。
设\(dp(i,j)\)表示考虑前\(i\)个点,有\(j\)个在\(s\)这边的方案数。(当然剩下的都在\(t\)边)
如果我们让\(i\)在\(s\)这边,就需要割掉它到\(t\)的边,这个代价是\(dp(i-1,j-1)+s_i\)。
否则,除了割掉到\(s\)的边,还需要割掉前面的\(s\)那边的点连过来的边,于是可得代价是\(dp(i-1,j)+p_i+jc\)。
注意这是CF,2s 1e8完全没问题。
不过有一个\(O(n\log n)\)的优秀做法。考虑一开始我们让每个点都割\(s\),接下来选择一些点改为割\(t\)。
一个点不割\(s\)而转为割\(t\),它的贡献是\(-p_i+s_i\)。
注意割\(t\)的话还需要割掉连向后面跟\(t\)相连的点的连边,这个点数我们也不确定是多少/yun
不过你发现如果我们直接按照\(n-i\)算,假设最后选了\(k\)个点,则会多算\(\binom{k}{2}\)次。我们枚举选了多少,这样就可以直接按照\(-p_i+s_i+c(n-i)\)排序来选,再减掉多算的。复杂度\(O(n\log n)\)。
CF793F Julia the snail
当然离线下来按\(r\)排序。你发现查询变成了某种单点查询,于是考虑修改对点的贡献。
然后发现对于梯子\(l,r\),如果\(i\)这个位置有\(l\leq ans_i\),那么我们把它推平成\(r\),其中\(r\geq l\)。容易发现这个操作比取\(\max\)要强,可以用吉老师线段树维护。(为什么说强?因为要足够强的操作才能带来正确的均摊复杂度)
CF802O April Fools’ Problem (hard)
雪 灾 与 外 卖
CF827F Dirty Arkady’s Kitchen
这题真**见鬼。
如果数据范围没这么大,一个显然的做法是分层图。但是数据范围有这么大就不好了。
注意到到达一个点的可行时刻大体看是一些区间,但是一个区间中间可能是断断续续的,这是因为每一时刻都必须走一步,可能会出现必须在一条边上来回走的情况。
我们进行拆点,拆成奇点偶点,分别只考虑奇数和偶数时刻的可达性,这样就可以把断断续续的变成区间。如果一条边开放,完全可以走过去走回来,所以如果\(i\)时刻\(u\)可达,那么\(i+2,i+4,i+6,...\)时刻都可达。当然同时我们也要拆边。
考虑按照边的出现时间从小到大处理。当我们加入一条边的时候,如果它的两端点都可达那就没啥事了,否则可以用一个去更新另一个,如果两个都不可达那就把它挂在这里,等有一个可达时再处理这条边。
我不知道是否可以转而维护边的可达性。
CF908H New Year and Boolean Bridges
注意到不可能有\(f(u,v),f(v,u)=0\),所以这个图弱连通。
A表示在同一个SCC,我们可以在链上加一条边,形成一个环,串起一个SCC。
O表示弱连通,所以没啥限制。
X表示不在同一个SCC。
你发现最多有23个大小至少是\(2\)的SCC
CF932G Palindrome Partition
考虑转成普通的回文!然后用PAM瞎做。
把右半边折过来,然后拍到一起,比如
| abc | de | f | f | de | abc |
变成
| abc | de | f\ |
| cba | ed | f |
拍成
| acbbca | deed | ff |
这就非常好。然后就变成了偶回文串划分计数。在PAM上跳fail来转移,或者直接用Manacher来判回文,容易做到\(O(n^2)\)。
然后是什么弱周期引理?不会,学了再补,咕咕咕。
类似于这个题的转化,还有一个奇妙的字符串题,说的是两个串lcp和lcs(suffix)的min,就是这两个串分别乱拼起来的lcp,这个乱拼方法是把123456789拼成192837465。
Day5
模拟赛
害 怕
今天又是挂分王!
T1 acquine
给一张完全图,每次询问一个子集的最小斯坦呐树。\(n\leq 21,q\leq 10^5\),边权在int范围内,256MB空间。
考虑对每个子集求出MST,然后做子集后缀和。
我写了个假上天的做法……直接随便钦定一个点,让它和剩下的点连一条边。然而这个钦定的点在MST上不一定是叶子,所以我就假了。
所以怎么做?
考虑Prim。
你发现256MB刚好开不下\(O(2^nn)\)个long long,但是刚好可以开int!我们预处理\(g(u,S)\)表示\(u\)到\(S\)的最小边权,那么就可以把转移优化掉一个\(n\)。
其实,如果你发现这个评测机机子不错,你就可以\(O(2^nn^2)\)硬草!dwt就这么过了/jy
T2 easy
给一个字符串,每次查询一个区间的本质不同子序列数量。\(n,q\leq 10^6\),膜1e9+7。
写了个1e5,字符集9的部分分。就是转成子序列自动机上路径计数,然后你发现这个dp可以用矩乘优化,这个矩阵大小是\(\vert\Sigma\vert+1\)。然后用线段树维护,矩阵乘向量,复杂度\(O(n\vert\Sigma\vert^3+q\vert\Sigma\vert^2\log n)\)。可以矩阵求逆+前缀和砍那个\(\log\),不过前面那个\(\vert\Sigma\vert^3\)确实太慢了。
正解是拆掉这个矩阵,变成非常奇妙的东西。反正我不会。
T3 trivial
给一棵树,每个点有一个颜色,求有多少选取两条无序路径的方案,使得两条路径没有交,并且每条路径的两个端点颜色相同(两条路径的端点颜色不必相同)。
有\(m\)次操作,每次ban掉一个点,不能选取这个点作为路径的端点。询问之间独立。\(n,m\leq 10^5\)。
考虑枚举一条路径,统计另一条。
直接算好像不是很容易,我们考虑反过来,算经过这条路径的路径数。
考虑如果另一条路径\((c,d)\)跟我们枚举的路径\((a,b)\)有交,一定有\(\mathrm{lca}(c,d)\)在\(a\rightsquigarrow b\)上,或者\(\mathrm{lca}(a,b)\)在\(c\rightsquigarrow d\)上。
画个图你发现我们可以用这两个东西把它们凑出来 : \(f(u)\)表示\(u\)子树内选两个点同色且经过\(u\)的方案数,\(g(u)\)表示整棵树内选两个点同色且经过\(u\)的方案数。对于\(\mathrm{lca}(a,b)\),经过它的路径数量是\(g(\mathrm{lca}(a,b))\);对于路径上其它点\(u\)是\(f(u)\)。
怎么求这两个鬼东西?可以对每种颜色建立虚树,然后对于一种颜色,它对虚树上一条边经过的所有点的\(f,g\)的贡献应该是相等的(当然对\(f\)和对\(g\)的贡献不相等),可以用一个树上差分来维护。
好了接下来就非常简单了!我们对\(f\)做树上前缀和(到根的链和),记为\(s\),然后选每一对\(a,b\)之后不合法的\(c,d\)数量就可以愉快差分出来,这个就是\(s(a)+s(b)-2s(\mathrm{lca}(a,b))+g(\mathrm{lca}(a,b))\),容易\(O(1)\)求得。总路径数就是\(S=\sum f(u)\),对于每对点,用总路径数减去上面的不合法的数量,再加起来就是答案。
这样我们就得到了一个\(O(n^2)\)的做法!
如何优化?考虑对于每一个\(u\),\(S-s(u)\)会被算 与\(u\)同色的点个数\(-1\) 次,可以直接干掉。主要问题在于\(s(v)-2s(\mathrm{lca}(u,v))+g(\mathrm{lca}(u,v))\),我们按照套路枚举lca统计答案。设这个lca是\(w\)(注意\(w\)不一定与\(u,v\)同色,但是一定在\(u,v\)颜色构成的虚树上)。
-
如果\(u=w\),那么只需要考虑\(s(v)\),这个\(v\)可以任意在\(u\)的子树里面选(,当然不能跟\(u\)相同),所以我们只需要记录每个点子树里面所有和它同色的点的\(s\)之和,这个可以再在虚树上dfs解决。
-
如果\(u\neq w\),考虑\(w\)的另一棵子树\(x\),\(x\)中所有与\(u\)同色的点都可以与\(u\)产生贡献。可以直接对每棵虚树上每个点\(u\),统计这棵虚树上\(u\)子树中所有颜色正确的点的\(s\)之和,然后每次用\(w\)的其它子树去更新一棵子树,可以在虚树上打标记然后下传。
等等现在我们还不支持ban掉一个点。
事实上只需要计算经过每个点的路径数量就可以了。你发现刚才算的就是这个/jy
唐椰叶写了5kb。不会有人想写吧/jy
期望得分100+80+10=190,实际得分8+80+10=98。T1挂惨了。
讲课
没有法法塔的多项式,和线性代数!
猫毒瘤/kel
随机数生成器
给一个随机数生成器(xorshift),给定种子,求第\(n\)次生成的数。2e5组数据,\(n\leq 10^{18}\)。
1
2
3
4
5
6
7
8
unsigned long long rand()
{
static unsigned long long seed;
seed^=seed<<13;
seed^=seed>>17;
seed^=seed<<5;
return seed;
}
看成系数膜\(2\),次数膜\(z^{32}\)意义下的多项式,然后就可以写出一个元素是多项式的矩乘,这就非常好。快速幂即可。
注意数据组数非常多,可以k进制矩乘来加速。
FJOI2018 城市路径问题
\(n\)个城市,第\(i\)个城市有\(2k\)个点权\((a_{i,1},a_{i,2},...,a_{i,k};b_{i,1},b_{i,2},...,b_{i,k})\)。
从城市\(u\)直接到\(v\)一共有\(\sum_{i=1}^ka_{u_i}b_{v,i}\)种方案,\(u\)可以等于\(v\)。
每次查询\(u\)不超过\(d\)步到\(v\)的方案数。
\(n\leq 1000,d<2^{31},k\leq 20,q\leq 50\),膜\(10^9+7\)。
做法很简单。考虑搞两个矩阵\(A,B\)分别是所有点的点权向量拼起来,当然其中一个要转置。你发现邻接矩阵就是\(AB\),幂就是\(ABABABAB...\)。
这个看起来就很有意思,我们把它改成\(A(BA)(BA)(BA)...B\),然后你发现\(AB\)是\(n\times n\)的,但是\(BA\)只有\(k\times k\),所以可以直接快速幂搞这个东西。复杂度\(O(q(n^2+k^3)\log d)\)。
循环矩阵行列式
题不是这样的!本来有一个Matrix-tree的皮。
\(n=2^m\)的矩阵\(A\)
\[A= \begin{bmatrix} a_0&a_1&a_2&\cdots&a_{n-1}\\ a_{n-1}&a_0&a_1&\cdots&a_{n-2}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_1&a_2&a_3&\cdots&a_0 \end{bmatrix}\],求行列式,膜\(998244353\)。
经典构造。
我们构造矩阵
\[M= \begin{bmatrix} \omega_{n}^0&\omega_{n}^0&\omega_{n}^0&\cdots&\omega_{n}^0\\ \omega_{n}^0&\omega_{n}^1&\omega_{n}^2&\cdots&\omega_{n}^{n-1}\\ \omega_{n}^0&\omega_{n}^2&\omega_{n}^4&\cdots&\omega_{n}^{2(n-1)}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ \omega_{n}^{0}&\omega_{n}^{2(n-1)}&\omega_{n}^{3(n-1)}&\cdots&\omega_{n}^{(n-1)(n-1)} \end{bmatrix}\]。首先这是一个范德蒙德矩阵。
为什么这么构造?因为循环矩阵\(A\)的转转转跟单位根的转转转放在一起会有奇妙的事发生!
我们设\(f(z)=\sum_{i=0}^{n-1}a_iz^i\)。
考虑\(AV\),你用脑子想象一下,发现它就是
\[AM= \begin{bmatrix} f(\omega_{n}^0)&f(\omega_{n}^0)&f(\omega_{n}^0)&\cdots&f(\omega_{n}^0)\\ \omega_{n}^0f(\omega_{n}^0)&\omega_{n}^1f(\omega_{n}^1)&\omega_{n}^2f(\omega_{n}^2)&\cdots&\omega_{n}^{n-1}f(\omega_{n}^{n-1})\\ \omega_{n}^0f(\omega_{n}^0)&\omega_{n}^2f(\omega_{n}^2)&\omega_{n}^4f(\omega_{n}^4)&\cdots&\omega_{n}^{2(n-1)}f(\omega_{n}^{2(n-1)})\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ \omega_{n}^0f(\omega_{n}^0)&\omega_{n}^{n-1}f(\omega_{n}^{n-1})&\omega_{n}^{2(n-1)}f(\omega_{n}^{2(n-1)})&\cdots&\omega_{n}^{(n-1)(n-1)}f(\omega_{n}^{(n-1)(n-1)})\\ \end{bmatrix}\]好像看到了法法塔!我们还需要一步 :
\[\vert AV\vert=\left(\prod_{i=0}^{n-1}f(\omega_{n}^i)\right)\vert V\vert\]这是为什么?考虑你选一个排列,它在每一行一定恰好选到一个,所以一定会乘一个\(\left(\prod_{i=0}^{n-1}f(\omega_{n}^i)\right)\),所以我们可以提出来,剩下的就是\(\vert V\vert\)了。
然后就可以两边除掉\(\vert V\vert\)。这样做的可行性,考虑范德蒙德行列式,因为\(\omega_n^k\)互不相同,这个行列式非\(0\),所以可以两边同时除掉。
于是我们就得到了
\[\vert A\vert=\prod_{i=0}^{n-1}f(\omega_{n}^i)\],可以使用法法塔计算。
数排列
给一个排列\(q\)和一个序列\(h\),定义一个排列\(p\)的权值
\[v(p)=\sum_{i=1}^n\sum_{j=i+1}^n([p_i>p_j]+[p_i+h_i\geq q_j])\],求有多少长\(n\)的排列\(p\)使得\(v(p)\)是偶数。\(n\leq 300\),膜\(998244353\)。
排列奇偶性,你想到了什么?
考虑偶数有\(1\)的贡献,奇数有\(0\)的贡献,就很不好。
考虑先乘个\(2\),最后除回来。然后变成偶数有\(2\)的贡献,奇数有\(0\)的贡献。这还不是很好。
接下来我们全\(-1\),最后加上一个\(n!\),这样偶数有\(1\)的贡献,奇数有\(-1\)的贡献。这就很好了。
答案的式子是\(\frac{n!+\sum_{p}(-1)^{v(p)}}{2}\),于是现在我们要计算\(\sum_{p}(-1)^{v(p)}\)。
你发现\(v(p)\)的式子里面第一个艾弗森括号是逆序对,第二个不知道是什么。不过我们可以把它拆出来。
\[\begin{aligned} &\sum_{p}(-1)^{v(p)}\\ =&\sum_{p}(-1)^{\sum_{i=1}^n\sum_{j=i+1}^n([p_i>p_j]+[p_i+h_i\geq q_j])}\\ =&\sum_{p}(-1)^{\sum_{i=1}^n\sum_{j=i+1}^n[p_i>p_j]}\prod_{i=1}^n(-1)^{\sum_{j=i+1}^n[p_i+h_i\geq q_j]}\\ =&\sum_{p}(-1)^{\sum_{i=1}^n\sum_{j=i+1}^n[p_i>p_j]}\prod_{i=1}^na_{i,p_i} \end{aligned}\]于是得到\(a_{i,j}=(-1)^{\sum_{k=i+1}^n[j+h_i\geq q_j]}\)。高消行列式即可。
CF1336E1
CF1336E2
九个sun
单位根反演,二项式定理。
复读机
EGF,单位根反演,多项式定理。
猫昕给了一个不用EGF的奇妙做法,不是很懂/kk
GF还是很好的工具吧/dk
爆炸oj3453 XLkxc
你发现里面是\(k+1\)次多项式,可以插值。
你发现中间是\(k+2\)次多项式,可以插值。
你发现外面是\(k+3\)次多项式,可以插值。
做完了/jy
NOI2019 斗主地
结论是,洗牌不会增加次数。换句话说,洗牌之前权值是几次,洗牌之后的期望权值还是那么多次。
这个结论是怎么得出来的?考虑
AGC020F Arcs on a Circle
随机游走
有一个醉汉站在原点,他有\(p_1,p_2,p_3,p_4\)的概率向四个方向走一步,求走\(n\)步之后他经过的点数期望。\(n\leq 50\),保留三位小数。
NOI2019 机器人
FJOI2021 外星飞碟
有一个数列\(a_1=0,a_2=1,a_n=\frac{na_{n-1}+n(n-1)a_{n-2}}{2}+(-1)^n(1-\frac{n}{2})\)。
求\(\sum_{i=1}^n\binom{n}{n-i}(n-i+1)a_i\),膜任意数。\(n\leq 10^{19},p\leq 11223372019\),时限10s。
看到递推式这个奇怪的东西你就觉得很不好。不过我们可以除一个\(n!\) :
\[\begin{aligned} a_n&=\frac{na_{n-1}+n(n-1)a_{n-2}}{2}+(-1)^n(1-\frac{n}{2})\\ \frac{a_n}{n!}&=\frac{1}{2}\left(\frac{a_{n-1}}{(n-1)!}+\frac{a_{n-2}}{(n-2)!}\right)+\frac{(-1)^n}{n!}+\frac{n}{2(n-1)!}+\frac{}{} \end{aligned}\]然后就可以考虑EGF/se
\[\begin{aligned} a_n&=\frac{na_{n-1}+n(n-1)a_{n-2}}{2}+(-1)^n(1-\frac{n}{2})\\ \frac{a_n}{n!}&=\frac{1}{2}\left(\frac{a_{n-1}}{(n-1)!}+\frac{a_{n-2}}{(n-2)!}\right)+\frac{(-1)^n}{n!}+\frac{(-1)^{n-1}}{2(n-1)!}\\ \hat{A}&=\frac{1}{2}\left(z\hat{A}+z^2\hat{A}\right)+e^{-z}+\frac{1}{2}ze^{-z}+\frac{z^2}{2}\\ 0&=\frac{z^2+z-2 }{2}\hat{A}+e^{-z}+\frac{1}{2}ze^{-z}+\frac{z^2}{2}\\ \end{aligned}\]杏仁
集合幂级数,将来补。
Day6
模拟赛
T1 breeze
原题CF838D Airplane Arrangements。
考虑没有座位这个事情很难受,我们在两边加两个座位,这样问题就变成了这两个新座位没有人坐。
两个座位也不是很好,我们把两个座位变成一个,此时变成了一个环。问题变成那一个座位没有人坐。不考虑限制一共有\((2(n+1))^m\)种情况。
你发现环是对称的,所以每个座位都有\(\frac{n-m+1}{n+1}\)的概率没有被坐,那么那一个座位没有人坐的方案数就是\(\frac{(2(n+1))^m(n-m+1)}{n+1}=2^m(n+1)^{m-1}(n-m+1)\)。
太奇妙了。这个技巧被称为 合链成环,这样做目的是利用环的对称性。
T2 midnight
不知道原题。可以在QingyuOJ http://oj.qingyu.us/problem/305 找到。
给两个基因串(只有AGCT)\(s,t\),求它们的最长循环同构子序列,或者说求一个串使得它是\(t\)的子序列,并且它和\(s\)的某个子序列循环同构。\(\vert n\vert,\vert m\vert\leq 2000\)。
LCS先转最长路,循环先破环成链。
现在问题变成,\((i,0)\)到\((i+n-1,m)\)的最长路的\(\max\)。
我已知有两种做法,不过都需要单调性。
唐椰叶的做法是,猜测这些路径不会互相穿过,于是用神秘分治把它们全搞出来。
具体怎么神秘分治?考虑我们求出\((mid,0)\)到\((mid+n-1,m)\)的最长路,然后这条路径就会把这个网格图分成两部分,左边的路径就不可能经过右边(但是可能经过分界线),右边的路径同理。所以维护一下这个图的形态,递归两边即可。复杂度\(O(nm\log n)\)。
官方题解做法是,用奇妙决策单调性,具体做法玄学,咕咕咕。
T3 cicada
原题loj6499。
静态序列,每次查询若干区间的并中有多少颜色。\(n,v\leq 10^5\),查询区间总个数不超过\(10^5\),空间8MB。
爆力Bitset。
按\(B=\Theta(\frac{n}{w})\)大小分块,这样一共有\(w\)块。爆力预处理每块的Bitset,空间复杂度是\(O(n)\)。
然后考虑查询的时候怎么快速搞。你发现合并一遍复杂度是\(O(n)\),绝对T飞了,所以我们需要预处理。
但是你又发现预处理一下空间是\(O(nw)\),MLE飞了,所以我们需要……
st表!复杂度变成\(O(n\log w)\),刚好卡过。复杂度\(O((n+q)\frac{n}{w})\)。
如果你的常数实在太大了,你发现后面还是T飞了。看起来搬题人或者出题人飞了。
诶T飞了吗?没飞,如果你试一试,发现可能好像只T了不到一倍的样子……不然就是你假了/cy
考虑一个常数优化,我们把所有只出现了一次的数搞出来前缀和统计,这样需要Bitset的值数量就只剩最多一半了,时空常数都变成一半,刚好可以通过。
期望得分40+0+20,实际得分0+0+20。
T1实在不能切不掉啊……
讲课
数论/jy
CC MAY15 Chef and Prime Divisors (CHAPD)
给\(a,b\),把\(b\)所有质因子次数变成\(1\)得到\(b^\prime\),问是否有\(b^\prime\vert a\)。\(a,b\leq 10^{18}\),1e4组数据。
考虑如果我们不是给\(b\)降次,而是给\(a\)升次,貌似也能得到正确的结果,因为每个质因子是独立的。所以我们求\(a^{114514}\pmod{b}\),如果是\(0\)说明可行。用快速乘+快速幂即可。
实际上那个次数不需要那么大,只需要到\(\log b\)即可。复杂度是\(O(T\log v\log\log v)\)。如果允许__int128或者认为long double快速乘是正确的,复杂度就是\(O(T\log\log v)\)。
loj NOI Round #1 失控的未来交通工具
还是使用 最大xor路径 的套路。
考虑每个环可以无限的走,同时因为取膜可以走负数次,于是我们看到了一个裴蜀定理。所有\(\gcd(s_i,m)\)的倍数都可以被取到,当然这里\(s\)是环长。
然后我们求出随便一条\(u,v\)的路径,比方说权值和是\(l\),那么接下来问题变成一个方程的解数计数 : \(x+bc\equiv l\pmod{m}\)。把\(x\)移过去解方程即可。
SDOI2013 随机数生成器 加强版
不保证\(p\)是质数。
考虑这个式子最后会是什么\(k^nx_1+b\frac{k^{n}-1}{k-1}\)(后面是等比数列求和),然后这个东西要同余于\(t\)。
乘过去
WC2020 猜数游戏
51nod1195 斐波那契数列的循环节
指数提升引理
斐波那契
CC OCT13 Fibonacci Number (FN)
IJPC2 Porter-Tele-Porter
CF990G GCD Counting
镜子
一个\(n\times m\)的棋盘,四周都是镜子,四角有接收器。现在从左下角发射一束激光,问它在被接收之前反射多少次。
这个问题太简单了,所以改成问你对于所有\(n\leq N,m\leq M\),那个次数的和。\(N,M\leq 10^7\),1e4组数据。
你打个表发现这个次数就是\(\frac{n+m}{\gcd(n,m)}-2\),然后枚举\(\gcd\)硬莫反即可。
lcm和gcd
https://shanlunjiajian.github.io/2021/04/05/a-problem-maybe-from-nowcoder/
又看了看好像做法一写错了……管他的(
NOI2016 循环之美
这个结论挺小学奥数,但是我没见过……
\(k\)进制下\(\frac{x}{y}\)既约且纯循环等价于\([x\perp y][y\perp k]\)。
Day7
模拟赛
T1 size
原题2013-2014 ACM-ICPC, NEERC, Northern Subregional Contest L
给一个几何体的主视图和左视图(在xz和yz上的投影),求它的最大可能体积。如果不可能输出-1。
保证这个主视图和左视图一定都是一段折线跟坐标轴围成的,所以用每个拐点的坐标给出。\(n,m\leq 10^5\),当然这里\(n,m\)指两个视图拐点数量。
考虑我们把两个视图沿法线拉伸成两个无限长的棱柱,那么它们的交就应该是最大体积。
拿一个水平面去截这个东西,然后积分。
根据上面那个棱柱交的思路,我们发现每次截出来的一定是若干矩形规则排列。具体怎么排列?看起来大概像这样 :
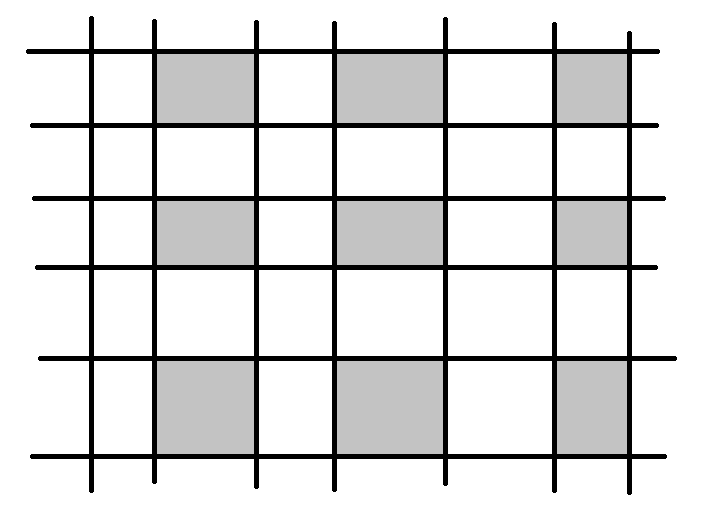
于是它们的面积之和就是在xz,yz上投影长度的积。
每个面上的投影长度,容易发现是一个分段函数,每一段都是一次函数。可以从上往下扫,每次遇到一个点就把它的贡献加入。这里需要一些数学技巧。
然后面积就是二次函数,可以直接积分得到体积。做完了。
T1.5
兔讲过,然后就换题了/jy
T2 number
T3 code
原题2015 ACM-ICPC World Finals L
有一个长\(n\)的随机串,每个字符都是abcd中的一个,具体是哪一个的概率给出。现在要进行二进制编码,使得所有可能出现的串都被编码,并且每一个的编码都不是另一个的前缀。求一种编码使得期望编码长度最小,输出最小长度。\(n\leq 20\)。
考虑不同的串可能有很多种,但是有很多种随机出来的可能性都是一样的,比如abcd和dcba。具体地,每种字符出现次数都相同,那么随机出来的概率相同。算一算你发现只有\(\binom{n+3}{3}\)种权值,大约是2e3以内。
这就很好,我们把这些东西打成Pair(权值,出现次数)扔进Huffman树,每次批量处理一个Pair的合并即可。具体地,如果出现次数是奇数,那就抽出一个重新扔回去,剩下的两两配对;如果是偶数直接配对;如果是\(1\),则从下一个里面抽出一个配对。
讲课
集训队作业选讲/jy
CF575A Fibonotci
对于大段进行快速幂,中断点特殊处理。
怎么处理?发现只需要支持查询区间矩阵积,不一定有逆所以上线段树,复杂度\(O(n+m(\log n+\log k))\)。
AGC039E Pairing Points
今天T3告诉我们20可能是\(O(n^{114514})\)的多项式复杂度!
考虑\(1\)跟哪个点配对,设为\(x\)。此时我们把这条线称为”轴线”,轴线把若干树串成一棵树,而这些树的线是互不相交的。
这就说明如果我们给删掉轴线之后的树们分别染色,那么从\(1\)走到\(x\),不管从圆上面还是下面走,经过的颜色序列相同,并且不会有颜色在一侧出现两次。
这启示我们按照区间为状态设计dp。设\(f(l_1,r_1,l_2,r_2)\)为\([l_1,r_1],[l_2,r_2]\)拼成一个森林的方案数,而\(dp(l_1,r_1,l_2,r_2)\)为拼成树的方案数。\(f\)的转移很简单,\(dp\)的转移可以枚举一条轴线把树们串起来。复杂度大概是\(O(n^6)\)之类的?
CF526G Spiders Evil Plan
一看就是长剖/jy
分别选两个直径端点作为根长剖求解,最后取\(\max\)。
考虑如果选过了\(x\),那么直接返回答案;否则要删去一个叶子换成\(x\)子树里最长的叶子,这个叶子要么是选的最短的叶子,要么是\(x\)往上跳遇到的第一个长链的叶子(换更高的一定不优)。
CF526F Pudding Mosters
收录于 CF再选做。
晚上的咋提宣讲。
背包II
无穷背包,容量1e18,重量和不超过1e5,不要求填满,求方案数膜\(998244353\)。两个方案不同定义为放的东西不同。
你发现是一堆\(\frac{1}{1-z^{w_i}}\)乘起来,所以我们可以分治呐塔塔求这个分母。然后就变成求多项式逆的某一项了。
怎么做?我们乘过去 :
\[\begin{aligned} F&=\frac{1}{a_0+a_1z+a_2z^2+...}\\ a_0F+a_1zF+a_2z^2F+...&=1\\ f_n&=\frac{1-a_1f_{n-1}-a_2f_{n-2}-...}{a_0} \end{aligned}\]变成了线性递推!然后硬搞就好了。
讲师给出了一个更普及组的做法。考虑二进制拆分,然后类似于数位dp设一个状态\(dp(i,0/1)\)表示考虑到前\(i\)位,现在跟\(m\)的大小关系是小于/等于。
发现因为东西很多,可能出现进位到前面的情况,所以我们需要额外记一位,设\(dp(i,0/1,k)\)表示进位到前面的部分是\(k\)。容易发现有\(k\leq 2\sum a_i\),因为即使一直进位也不可能进出超过两倍。
然后你发现这个dp的转移可以用法法塔优化,就做完了,复杂度\(O(n\log^2 n)\)。
CCPC2018 Jilin The Hanged Man
树,每个点有两个点权\(a,b\),对于每个\(x\in[1,m]\),求有多少独立集满足\(a\)之和等于\(x\),并且\(b\)之和最大。\(n\leq 50,m\leq 5000\)。
重链剖分优化状压dp/jy
考虑爆力dp就是按照dfs进行转移,设\(dp(u,S)=(k,c)\),其中\(S\)表示前面所有点选/不选的状态,\(k\)是最大值,\(c\)是最大值计数。
CCPC2019 Qinhuangdao Game on Chessboard
有一个棋盘,一开始每个位置有一个黑色或白色的棋子,每个棋子有一个权值。每次可以删掉一个棋子或者一黑一白两个棋子,删一个的代价是它的权值,两个的代价是它们权值差的绝对值。可以删一个棋子当且仅当它左下方没有棋子。\(n\leq 12\)。
考虑轮廓线dp,我们状压左下方已经删掉区域的轮廓线,然后枚举即可。
这个轮廓线状态数是\(2^{24}\),直接转移过不去。不过其中只有\(\binom{2n}{n}\)种有用,剪枝一下就可以过了。复杂度\(O(2^nn^2)\)。注意更新轮廓线通过一点推导可以做到\(O(1)\)。
ICPC2020 Shanghai F Fountains
给一个序列,定义\(S(l,r)\)是区间和,对于所有\(k\in[1,n(n+1)/2]\),求出选\(k\)个区间\([l_i,r_i]\)的方案,最小化下面的式子 :
\[\sum_{1\leq L\leq R\leq n}\left(S(L,R)-\max_{L\leq l_i,r_i\leq R}S(l_i,r_i)\right)\]。\(n\leq 9\),序列非负。
这是个轮廓线dp/jy
先把那堆区间和都干掉,问题变成最大化每个区间里面选的区间的\(\max\)的和。
把区间看成平面上的点\((l,r)\),区间和变成点的权值,然后所有区间构成一个\(y=x\)上方的三角形,区间的包含关系\(L\leq l,r\leq R\)就是\((l,r)\)在\((L,R)\)的右下方。
然后轮廓线来了。考虑非负说明一个点比它右下方的点都要优,所以我们从左上往右下dp,状压一条轮廓线表示已经处理的区间,这些区间已经计算了它们的\(\max\)。换句话说\(dp(i,S)\)表示已经选了\(i\)个点,轮廓线\(S\)左上方所有点右下方最大的点的权值和。
CERC2017 B Buffalo Barricades
平面上有一堆牛,接下来有一些牛仔要空降,每个牛仔会从他空降的位置往下、往左发射一道围栏,这道围栏直到撞到坐标轴或者撞到之前牛仔的围栏才会停住。求每个牛仔围住了多少牛。\(n,q\leq 3\times 10^5\)。
考虑每个牛可能被围住很多次,这就很不好。
我们时间倒流,先计算最后每个区域有多少牛,
ICPC2020 Shanghai J Octasection
给\(n\)个长方体,用三个分别平行于xy,xz,yz的平面去切割,使得每个长方体都被至少一个面切到,这里的切到指的是有交而不是相切。\(n\leq 10^5\),构造方案。
shy(出题人) : 我才写了16k
shy : 1h就写完了。但是调了3h!
当然先全离散化。
这三个平面我们称为z,y,x。
首先每个平面都可以用一个点确定。
枚举第一个平面,然后删去所有被它切到的长方体,问题变成二维的。
然后考虑剩下两个直线(三维中是两个平面)的交点,你发现从每个矩形引一个井字形,如果这个点选在这个井字形里面那这个矩形就可以,否则就不行。所以变成了井字形求交。
井字形的交太**恶心了,我们转而维护不可行区域的并。不可行区域是矩形四个点引出的四个2-side区域。这个点选在不可行区域内那就不行,否则可行,这就很好。
注意到如果我们把扫第一个平面的过程当成时间维,那么每个点出现的时间都是一个前缀和一个后缀,当然这是废话。线段树分治硬上可以直接干翻这个东西。不过这是俩\(\log\),我们有更好的方法!
考虑对于四个方向分别维护四条边界线,或者你喜欢叫轮廓线也可以。最后问题就是这四条边界线围起来的区域里面有没有点。
加一个点或者删一个点怎么维护?你发现删点导致一个点变到边界线上的时间是一个区间,因为每个点删掉的时间是一个区间,所有遮住这个点的点删掉的时间就是这些区间的交,所以每个点在边界上的出现消失都是\(O(1)\)次,用扫描线+BiT预处理出来,set维护即可。
然后考虑怎么维护里面的区域有没有点。可以搞一个\(M\times M\)的大框,对于每个\(y\)维护左边两条边界线到左边框的距离加上右边两条边界线到右边框的距离,如果存在某个\(y\)的结果\(\leq M\)那就可行。
你我可能会说这个开一棵线段树维护\(\min\)就好了嘛!但是每条边界线有均摊性质,边界线的并则没有,也就是说对于比如左上和左下边界线,删掉左下的一个点,可能使本来在整个边界线左边的、属于左上边界线的点露出来,这对整个边界线的影响是难以预处理或者快速计算的。
进一步考虑每个\(y\)上面对\(x\)的限制由谁提供。上界可能是右上,右下边界,下界可能是左上,左下边界。于是我们对于它们两两拼成的四种情况(右上+左上,右上+左下,右下+左上,右下+左下)分别用一棵线段树维护\(\min\),那么边界线上每次变化现在确实体现在所有线段树上的\(O(1)\)次区间加。然后考虑合并这四棵树的信息,最后每个\(y\)的结果就是四棵线段树维护结果的\(\max\),可以搞一个堆维护最小值,四棵线段树上每次操作之后都在堆上更新一下。复杂度一个\(\log\)!
然而std是俩\(\log\)的,原因是维护边界线用的是set,shy直接在set上二分了。
shy : 听懂了你们要把它写出来啊
兔 : 啊?没听懂没听懂/jk
shy : 没听懂也要把它写出来啊
shy : 我们找个同学来复述一下
大家 : 唐-椰-叶-!
于是唐椰叶复述了一遍/xia
Qingyu : 能不能做四维啊
兔 : 别他妈扯了……
Day8
模拟赛
T1 cycle
原题CF722F。
显然exCRT。
容易想到双指针。
exCRT要支持删除,需要快速查lcm,这里可以分解质因数,然后对每个质因数打单调队列。当然你可以爆力线段树/st表。
另一种做法是分解质因数进行考虑,对于每个质数幂维护膜它的一个限制。
T2 fade
原题CF1063F。
根号做法非常简单,可以直接参见题解。
有一个1\(\log\)做法,请见sdptt22 r3 D2的讲课第一题。
T3 graph
原题CF814E。加强到\(n\leq 1000\)。
考虑最短路树,实际上这里就是bfs树。你发现有一棵bfs树之后,剩下的所有边一定都连在同一层的点之间,否则最短路就不唯一了。
同时因为最短路随编号单调递增,所以每一层都是一个区间。
容易发现第\(0\)层只有\(1\),第\(1\)层是\([2,d_1+1]\)。
每层内部可以相互连边,每层每个点必须向上一层恰好一个点连边。
待补,咕咕咕。
期望得分100+0+4=104,实际得分50+0+0=0。我是垃圾。
讲课
构造&咋提。
猫 : 你做一般的题可能要观察甚至挖掘性质,但是做构造题你可能要抛弃性质。
AGC030C Coloring Torus
这题就是强行构造。考虑我们需要让每个同色块周围的各种颜色个数相同,不如直接让它们周围环境完全相同。
容易发现\(k\leq 1000,n\leq 500\)看起来是让你在棋盘上放下边长两倍的颜色。
容易想到直接一行填一个颜色,这样可以放\(n\)种颜色。接下来对于某些行我们炸开它,然后在里面隔一个加入一个新颜色,这样就可以放\(2n\)种了。
现在有两个问题,一个是\(n\)是奇数的时候会出现自己撞自己,一个是\(k\)是奇数的时候一定有一行是纯色的,这一行就不满足条件。
第一个显然容易解决,第二个看起来不是很容易解决。
所以我们要换方法。对于四连通,我们容易想到把横着的线换成斜着的线,也就是把格子按照\((x-y)\bmod{n}\)的值分类,每一类在一条斜线上,此时一条线上相邻两个点变得不相邻,并且每个点和旁边线上两个点相邻。
然后你发现此时,刚才的炸开操作就变得好了起来,我们莫名其妙地解决了刚才的第二个问题。
AGC027D Modulo Matrix
显然取所有的\(\max\bmod{\min}=1\)。
黑白染色,不妨钦定白格子较大。如果白格子膜四周的黑格子都是\(1\),白格子可以取四周的\(\mathrm{lcm}+1\)。
每个黑格子还要分配权值。因为要让\(\mathrm{lcm}\)不相同,我们容易想到取一些质数。
黑格子数量足有\(125000\),直接取前面这么多个质数显然会爆\(10^{15}\)。
考虑到\(10^{15}\)开四次根大概是\(10^4\)少一点,这个\(10^4\)有什么用呢?
考虑给需要的质数数量开根号。那就是给每个黑格子分配两个质数的积,然后让白格子里求\(\mathrm{lcm}\)的时候把相同的质数抵消掉,最后只剩下四个质数的积。
不妨让它把相邻的格子的相同质数抵消掉,那就是要斜着相邻的格子共用质数,这个斜着相邻可能是左上-右下或者左下-右上。所以我们给每条斜线分配一个质数,每个黑格子的数就是它所在两条斜线质数的乘积。做完了。
AGC025D Choosing Points
结论 将距离是\(\sqrt{d}\)的点对连边,得到二分图。
证明 因为\(d\)是二平方和,我们经典地对\(d\)膜\(4\)的值分类讨论。
-
\(d\bmod{4}=3\),不存在任何边。
-
\(d\bmod{4}=1\),我们直接黑白染色。那么黑点和白点的两维差,一定一维是奇数一维是偶数;黑点和黑点、或者白点和白点的两维差,一定都是奇数或者都是偶数。那么膜\(4\)得\(1\)的边,一定是连接黑点和白点。
-
\(d\bmod{4}=0,2\),可以考虑\(d^2=2\)的情况,发现是一个斜着的网格。于是我们可以转\(45\)度,然后乘上\(\frac{\sqrt{2}}{2}\),就相当于将\(d\)除了\(2\)。如此递归,一定会递归到一个\(d\bmod{4}=1,3\)的情况。
所以我们可以连续染两次,做完了。
CF1270E Divide Points
跟上面那题证明过程一样。
直接黑白染色。
如果既有黑点又有白点那就很好,因为是二分图就说明所有黄边的平方都是偶数,而蓝边都是奇数,它们必不相同。
否则就说明任意两点距离平方都是偶数,于是我们就可以选一个点作为原点,然后按照上面的做法转转转递归下去,这显然不会影响答案。这样递归最多\(\log\)次就会停止,复杂度\(O(n^2\log v)\)。
CF547D Mike and Fish
把点看成连在xy坐标之间的边,把染色看成边的方向,然后直接欧拉回路。
AGC017E Jigsaw
我们从左往右考虑。如果一个拼图的\(c\)是\(0\),那么它需要被一块\(c=\)它的\(a\)的拼图压住,或者直接接地;否则它需要被一块拼图托起来。\(d\)同理。第一种我们称为插座,第二种是插头。
然后我们就可以建立一张图,用\(2H\)个点表示不同高度的插座和插头,然后每个拼图看成一条边,连接它两边插座/插头对应的两个点。以左边为例 :
-
如果\(c=0\),从\(a\)连过来,表示有一个高\(a\)的左插座,需要一个高\(a\)的右插头
-
否则,从\(-c\)连过来,表示有一个高\(c\)的左插头,需要一个高\(c\)的右插座
-
如果\(d=0\),连向\(-b\),表示有一个高\(b\)的右插座,需要一个高\(b\)的左插头
-
否则,连向\(d\),表示有一个高\(d\)的右插头,需要一个高\(d\)的左插座
你发现恰好对应了起来。跑欧拉回路即可。
具体地我们建两个虚点表示开头和结尾,对于度数不对的点我们连向虚点。
注意每一连通块都需要有至少两个点和分别和两边的虚点连边,如果没有这样的点就可以判无解。
AGC037D Sorting a Grid
反着考虑。如果最后一步要排成正确的,我们需要先保证前两步中每个数都到了正确的行上。
然后你发现第一步只改变每个数所在的列,所以只能用第二步来把每个数放到正确的行上,这样第一步的工作就是保证每个数放到正确的列上。
对于每一行进行染色,也就是对于除\(m\)下取整的值进行染色。我们要求第一步之后,每列每种颜色恰有一个。
考虑建图,对于每个元素,从它一开始所在的行连向它的颜色,然后问题转化成求\(n\)次二分图完美匹配。
你发现我们建出来的是一张二分完全图,所以一定是正则二分图。如果我们每次跑Dinic得到一个完美匹配,然后删掉它,剩下的还是一个正则二分图,于是根据Hall定理可以知道接下来仍有完美匹配。复杂度\(O(n^{2.5})\)。
下面是咋提。
Treap
求\(n\)个点,附加权值在\(1,...,n\)的排列中随机选取的Treap的结点深度平均值期望。\(n\leq 10^{15}\),1e6组数据,保留7位小数。
龙 与 地 下 城
容易求出来这个期望是\(2\left(1+\frac{1}{n}\right)H_n-3\),然后进行数据分治,小数据预处理,大数据直接使用\(\ln\)近似\(H\)。
FJOI2013 圆形游戏
考虑这个东西形成了一个树形结构,最后相当于有一棵森林,每次可以砍掉一个点和它的子树。
森林不是很好,我们加一个虚根,但是这个点不能删。于是我们可以把砍掉子树变成砍掉边之后保留根所在的连通块。
这个博弈游戏有个名字叫Hackenbush。
Hackenbush有两个版本,Green Hackenbush和Red-Blue Hackenbush。前者是平等博弈,后者是不平等博弈。这里显然是前者。
引理 一个点子树的SG值是所有儿子子树SG值的\(\mathrm{xor}\)再\(+1\)。
证明 归纳即可,自证不难。反正我模拟赛搞出来了/jy
翻硬币游戏
一些硬币从左往右排开,每一个都可能是正面或者反面。每个硬币有一些关联硬币,这些关联硬币都在它左边。
如果你选择翻第\(i\)个硬币,你可以一起翻它的关联硬币,具体怎么翻由你决定。
现在Alice和Bob要玩翻硬币,Alice先手,每次只能选择一个正面朝上的硬币,进行如上的操作。问谁必胜。
结论 局面的SG值为每个正面朝上的棋子单独正面朝上时SG值的异或和。
证明 直接归纳即可。
所以我们就得到了一个简单的dp。
CF1149E Election Promises
让你想起CF1451F。
于是考虑怎么划分状态。没啥想法。
JOISC 2020 Day3 星座 3
EIOI FJOI2020 异构序列码性态问题
打表你发现,\(n=4\)的时候只有3 1 4 2和3 2 4 1不能得到。
然后继续打表,你发现所有不能得到的序列,都存在一个离散化后与上面两个序列同构的子序列。
Day9
模拟赛
T1 sum
给一个序列\(a\),支持单点修改,求某个区间单独拿出来,求\(k\)阶前缀和得到的最后一项。\(n\leq 10^5,k\leq 8\)。
正解是\(O(nk\log n)\),但是我有一个\(O(nk^2\log n)\)的做法(
容易想到拆贡献,打表发现\(i\)对右端点\(j\)的贡献是\(a_i\binom{k+j-i-1}{j-i}\)。考虑组合意义,就是在一张网格图上从\((i,1)\)走到\((j,k)\)的方案数。
考虑线段树维护一个dp,每个点维护\(f(i)\),表示从区间中所有\((j,1)\)走到\((r,i)\)的方案数。合并的时候,我们让右儿子直接加上贡献,然后左儿子乘一个组合数转移。复杂度就是\(O(nk^2\log n)\)了。
T2 fall
原题CF781E。
有一块木板划分成\(w\)段,上方有\(n\)块挡板,每一块恰好覆盖了\([l_i,r_i]\)段,高度是\(h_i\),有一个强度\(s_i\)。
现在从极高处\(h+1\)扔下一些球(当然所有挡板都比极高处低),每个球撞到挡板会分裂成两个,从挡板的两边落下去。如果一个挡板左边贴着左边界,分裂的两个球都会从右边掉下去;反过来也是。
这个挡板非常智能,如果一个球从\(>h_i+s_i\)的高度掉下来,挡板为了避免被砸坏,会让且仅让这个球穿透过去,球的运动不会受到任何影响(也就是说它的下落高度不变,也不会分裂)。
求最后多少球落到地上。\(h\leq 10^9,w\leq 10^5\)。
从上往下处理挡板。考虑一个板子会干什么 :
-
把能接住的球接住,统计个数
-
往两边分别扔这么多球
所以,数据结构维护横轴,需要支持
-
查询区间内有多少高度在某个值以下的球,并把它们删掉
-
往一个横坐标插入一堆球
一堆球就很不好,我们可以用一个Pair(高度,个数)来存。
每个横坐标开一个堆,线段树维护区间\(\min\)来判断要不要递归下去删除即可。
实际上不需要堆,因为插入的高度递减,栈即可。
复杂度\(O(n\log n)\)。
T3 message
原题CF Gym101221F,2014 ACM-ICPC World Finals F. Messenger
有两个点\(A,B\)在平面上沿两条折线运动。两个点同时开始运动,速度都是\(1\),并且到达终点之后立刻消失。
\(A\)要给\(B\)发消息。\(A\)会向某个方向发出一条消息,消息可以看成一个点\(C\)。然后\(C\)会沿一条射线运动,速度也是\(1\)。\(B,C\)重合时\(B\)会接收消息\(C\)。
求消息\(C\)移动的最小距离。\(n,m\leq 5\times 10^4,x,y\leq 10^6\),其中\(n,m\)是两条折线的点数。
我们设\(A_t\)表示\(t\)时刻的\(A\)点位置,\(B_t\)同理。
考虑时刻\(t+d\)可行,当且仅当存在\(A_tB_{t+d}=d\)。
看到这个问题就想到二分答案\(d\),但是直接这么搞不一定具有单调性,我们改一下变成\(A_tB_{t+d}\leq d\)。
如果存在一个\(t\)使得这个式子成立,那么一定存在一个\(\leq d\)的解,否则一定不存在。这非常直觉,但是怎么证明?不知道,最后再说。
然后变成了判断有没有解。我们设一个新的折线\(P_t=A_t-B_{t+d}\),那么存在\(A_tB_{t+d}\leq d\),等价于存在\(P_tO\leq d\),当然\(O\)是原点。求一条折线到原点的最小距离,就是对于每条线段求到原点的最小距离然后取\(\min\),这个很好做。
于是复杂度就是\(O(n\log v)\)。
所以那个结论怎么证?显然的感性证法是先放宽限制允许选择曲线,然后利用折线的连续性,把曲线伸直。但是这太感性了。dwt给出了一个看起来很对的证法,大家可以前往他的博客康康。
期望得分100+100+1=201,实际得分100+100+10=210。
不知道哪位朋友往法塔爬上扔了qec,qsc,qsc,qwc,qlc,qqc,qbc,导致lyh把qyc也干掉了……
讲课
还是集训队作业。
CF582E Boolean Function
WC T2/jk
先表达式树。
考虑设\(dp(u,S)\)表示\(u\)子树内搞完了,对于第\(i\)个限制我们得到\(S_i\)的方案数。
直接转移会T飞,发现转移是and/or卷积,法哇塔即可。
CF568E Longest Increasing Subsequence
设\(dp(i,j)\)表示\(a_1,...,a_i\)的长\(j\) LIS中,最后一个数最小是多少。
发现对于每个\(i\)只会有一个\(dp(i,j)\)发生变化,这个东西可以二分。
考虑如果这个位置是确定的,可以直接转移。否则,我们直接枚举最小可以填哪个数,然后填上。这里爆力的复杂度是\(O(km)\),由于是CF完全可以跑。
注意到这里的LIS是严格的,所以不可能选一个数两次。
至于构造方案,我们就先找到LIS包含的位置,然后贪心填;剩下的位置随意。
CF521D Shop
收录于……忘掉了,反正收录过/cy
CF585F Digits of Number Pi
数位dp。先差分。
然后考虑建立SAM以匹配子串,枚举当前要计算的长度,设\(dp(i,u,flag=0/1,lim=0/1)\)表示长\(i\),走到\(u\),是否已经匹配了足够的长度,是否达到上界的方案数。爆搜即可。
实际上这个SAM可以用ACAM代替,可能有人觉得写起来更简单?
CF575I Robots Protection
先考虑\((x,y),(x+l,y),(x,y+l)\)的机器人。
考虑这个机器人能保护\((a,b)\),当且仅当
- \[x+y\leq a+b\leq x+y+l\]
- \[x\leq a,y\leq b\]
你发现第一个限制描述了一个斜着的条,第二个描述了一个右下1/4平面。
第一个限制很容易统计,我们可以直接每条斜线开一个BiT来做。
考虑容斥,用满足第一个的减去满足第一个而不满足第二个的。
你发现第二个也很容易统计,因为是一个平行四边形,可以直接用二维BiT。做完了。
CF587D Duff in Mafia
套娃机。
二分答案,然后进行2-SAT,并需要优化建图。2-SAT优化建图已经在咕了!
CF587F Duff is Mad
兔讲过(
CF571D Campus
奇妙差分。
不考虑清零操作,而是将每个询问拆成两个,每个询问的答案就是当前值减去上一次被清零时的值。注意这两个值都是不计清零的。
然后 当前的值 和 上一次被清零的时刻 都可以在启发式合并的时候很容易地维护,实际上你想线段树合并也没啥问题。
CF536D Tavas in Kansas
发现有用的距离实际上只有\(2n\)个,可以爆力dp,也就是设\(dp(i,j)\)表示A选到\(i\),B选到\(j\),A的得分减去B得分的最大值。
转移发现可以前缀和优化。
CF611H New Year and Forgotten Tree
强行构造。我们把点分成1到6位,然后可以注意到把每一类点缩起来一定得到一棵树,不然说明有环。
所以我们可以每一类钦定一个特殊点,让特殊点连成一棵树,剩下的边全都在每一类点之内。
所以接下来所有的边都变成在同一类点中的了。
CF528C Data Center Drama
收录于……鬼知道,反正收录过。
CF613E Puzzle Lover
路径只可能是,中规中矩地往一边走并绕回来,然后在另一边瞎走,然后往另一边继续走并绕回来。这三部分都可能只有\(0\)步。
分别处理这三种情况(实际上考虑不同的方向,是四种),可以用一个dp解决。
CF538G Berserk Robot
第一步非常妙。先转45度,\((x,y)\rightarrow(x+y,x-y)\),这样每走一步两维的变化只可能是\(\pm 1\),而不可能有\(0\)。
然后就变成了两个一维的问题。我们重新定义\(x\)为转化后一维问题中的坐标。
下一步是,考虑把\(x\)变成\(\frac{x+t}{2}\),\(t\)是时间。这样就把\(+1,-1\)变成了\(+1,0\)。
考虑如果知道了每一轮的位移\(d\),就可以很容易地解决剩下的问题。
然后考虑有解当且仅当任意\(i<j\)满足\(x_j-x_i\leq j-i\),而\(x_i,x_j\)都是关于位移的一次函数,比如对于\(x_i\)有\(x_i=d\lfloor\frac{i}{l}\rfloor+x_{i\bmod{l}}\)。所以我们可以得到一些关于\(d\)的线性不等式,解一下得到一个
CF566C Logistical Questions
发现是凸的,所以我们在静态Top tree上二分,复杂度\(O(n\log n)\)/jy
实际上有更简单的方法。点分治,要选择递归到哪一个儿子,可以求出走过去的变化量,这个使用导数容易算出来。利用凸性容易证明这样做的正确性。
Day10
模拟赛
T1 permutation
推了四个半小时,发现假了/cy***!***。
原题CF840C。
给一个序列\(a\),求有多少重排方式,使得重排之后任意相邻两项的乘积不是完全平方数。\(n\leq 300\)。
考虑 乘起来得到完全平方数 是一个等价关系,所以我们可以得到一堆等价类。问题变成相邻的不能在一个等价类。
容斥。我们把球看成无序的,最后乘上各等价类的阶乘
T2 route
原题。
平面上有一个点的序列\(A\),你现在要从\(A_1\)出发走到\(A_n\)。如果\(i,j\)之间的所有点都距离\(A_iA_j\)不超过\(d\),那么你可以一步从\(A_i\)走到\(A_j\)。求最小步数。\(n\leq 2000\)。
显然的dp是\(dp(i)\)表示走到\(A_i\)的最小步数。
T3 game
原题CF674F。
有\(n\)个人,
这题最妙的地方就是,我们根本不需要研究怎么构造方案。
发现一共有\(\sum_{i=0}^{\min(n-1,p)}\binom{}{}\)种方案
期望得分0+0+0=0,实际得分0+0+0=0。
讲课
CF670E Cross Sum
考虑一个更弱的问题 : 如何找到第\(m\)近的交点。
二分答案,然后画一个圆。如果两条直线跟圆的交点分别是\(a,b,c,d\),那么两条直线的交点在圆内,等价于\(a<c<b<d\)。
于是我们可以离散化+BiT维护这个东西。
然后我们得到了第\(m\)近的交点。然后呢?
注意到\(m\)很小,于是我们继续画圆,然后爆力找到所有圆内的交点即可。
CF674G Choosing Ads
考虑一个”出现次数超过一半的数”的经典做法,我们每次删掉\(\lfloor\frac{100}{p}\rfloor+1\)个不同的数,这样出现超过\(p\%\)的数一定会被留下来。
发现这个过程可以用线段树维护,就非常好。
AGC034F RNG and XOR
AGC038E Gachapon
min-max容斥。考虑怎么计算至少有一个数够了的期望时间。
AGC034D Manhattan Max Matching
考虑曼哈顿距离本身就是取\(\max\),具体地,\((x_1,y_1)\)和\((x_2,y_2)\)的曼哈顿距离是下面四个东西的\(\max\) :
- \[x_1-x_2+y_1-y_2\]
- \[x_2-x_1+y_1-y_2\]
- \[x_1-x_2+y_2-y_1\]
- \[x_2-x_1+y_2-y_1\]
于是我们就可以拆开绝对值。
接下来按颜色建两排点,按照上面的方式连边,也就是建立四个点分别表示取四种贡献,并红蓝点分别向这个四个点连边。
最大费用最大流即可。
CF704E Iron Man
考虑二分答案,然后差分成天天爱跑步。然后这个感觉失败了,因为差分之后问题就是交点个数了,而交点个数看起来非常复杂。
考虑树剖,然后变成链,链上就好做了。每个人是一条线段,在链上扫时间,用平衡树维护相对顺序,然后用一个可删堆维护相邻线段的交点,如果在一条线段删掉之前达到了交点,那就撞上了。复杂度\(O(n\log^2 n)\)。
CF674D Bearish Fanpages
还记得Qtree里的一道link-cut,同色连通块大小吗?
考虑在父亲处处理儿子们的信息,就做完了。
AGC033E Go around a Circle
冷 静 分 析
假设\(s_1\)是R,否则可以全部反过来。于是我们知道 结论1 环上不可能出现两个连续的B,证明 否则选在两个B中间开始就无了。
你发现这个完全不充分,它只是必要。
不过对于一种情况它是充分的 : 整个串只有R,没有B。这可以特判掉,接下来我们假设串里有B。
另一个结论 : 环上一段连续的R长度一定是奇数。如果是偶数,那么环上任意一个点到两个端点的距离奇偶性相同。考虑串