感觉完全没啥用啊。
呃口胡了一套智障符号化方法。
例题只有一道,所以算是还在施工吧。
换根dp解决一类性质比较好的子树为阶段的dp,其中看起来需要以每个点为根做一遍dp,不过实际上可以只dp一遍,然后通过父亲之类点的信息快速推出当前点为根的dp值。
我们设\(dp_r(u)\)表示以\(r\)为根时\(u\)的\(dp\)值,那么显然有
子树不变的结论 如果以\(u\)为根时,\(v,w\)在\(u\)的同一棵子树,那么以\(v,w\)分别为根时,\(u\)的子树不变,此时\(dp_v(u)=dp_w(u)\)。
子树不变是这一方法推式子的核心。
好了,让我们来
试看看!例题1.7
CF1375G Tree Modification
式子是
\[dp_r(u)=\sum_{v\in\mathrm{ch_r}(\mathrm{ch_r}(u))}(dp_r(v)+1)\]。这里的\(\mathrm{ch}_r\)当然是以\(r\)为根时的儿子集合。我以前都是用\(\mathrm{son}\)来着,不过那个现在感觉不如\(\mathrm{ch}\)舒服?
这个怎么做?先求出每个点的\(dp_1\),然后假设已经求出了\(dp_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{fa}(\mathrm{fa}(u)))\),我们从\(\mathrm{fa}(\mathrm{fa}(u))\)换根
\[dp_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{fa}(\mathrm{fa}(u)))=\sum_{v\in\mathrm{ch}_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{ch}_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{fa}(\mathrm{fa}(u))))}(dp_{\mathrm{fa}(\mathrm{fa}(u))}(v)+1)\]看起来很眼花缭乱。画画图,感觉我们可以把这个东西拆开,拆成三部分
- \[\color{red}{S_1}=\mathrm{ch}_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{ch}_{\mathrm{fa}(\mathrm{fa}(u))})\cap\mathrm{ch}_u(\mathrm{ch}_u(u))\]
- \[\color{blue}{S_2}=\mathrm{ch}_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{ch}_{\mathrm{fa}(\mathrm{fa}(u))})-S_1\]
- \[\color{green}{S_3}=\mathrm{ch}_u(\mathrm{ch}_u(u))-S_1\]
这三个集合的大概,可以画一张图表示 :
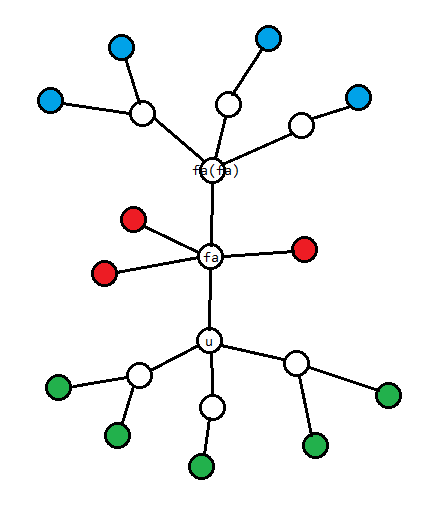
然后我们就可以得到\(dp_u(u)\)和\(dp_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{fa}(\mathrm{fa}(u)))\)的简洁式子
\[\begin{aligned} dp_u(u)&=&(dp_u+\mathbf{1})&(\color{red}{S_1}+\color{green}{S_3}+\mathrm{fa}(\mathrm{fa}(u)))\\ dp_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{fa}(\mathrm{fa}(u)))&=&(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})&(\color{red}{S_1}+\color{blue}{S_2}+u) \end{aligned}\],当然这个符号说的是一个集合的函数值之和。同时你还可以发现这样两个事情
\[\begin{aligned} dp_u(\mathrm{fa}(\mathrm{fa}(u)))&=(dp_{u}+\mathbf{1})(\color{blue}{S_2})\\ dp_{\mathrm{fa}(\mathrm{fa}(u))}(u)&=(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{green}{S_3}) \end{aligned}\]。然后考虑子树不变,你发现
分别以\(1,u,\mathrm{fa}(\mathrm{fa}(u))\)为根的时候,\(\color{red}{S_1},\color{green}{S_3}\)的子树都不变;
分别以\(u,\mathrm{fa}(\mathrm{fa}(u))\)为根的时候,\(\color{blue}{S_2}\)的子树不变;
分别以\(1,\mathrm{fa}(\mathrm{fa}(u))\)为根的时候,\(u\)的子树不变。
然后我们用上面的东西化式子,得到
\[\begin{aligned} dp_u(u)&=(dp_u+\mathbf{1})(\color{red}{S_1}+\color{green}{S_3}+\mathrm{fa}(\mathrm{fa}(u)))\\ &=(dp_u+\mathbf{1})(\color{red}{S_1})+(dp_u+\mathbf{1})(\color{green}{S_3})+(dp_u+\mathbf{1})(\color{blue}{S_2})+1\\ &=(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{red}{S_1})+(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{green}{S_3})+(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{blue}{S_2})+1\\ &=(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{red}{S_1})+dp_{\mathrm{fa}(\mathrm{fa}(u))}(u)+(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{blue}{S_2})+1\\ &=(dp_{\mathrm{fa}(\mathrm{fa}(u))}+\mathbf{1})(\color{red}{S_1}+\color{blue}{S_2}+u)\\ &=dp_{\mathrm{fa}(\mathrm{fa}(u))}(\mathrm{fa}(\mathrm{fa}(u)))\\ \end{aligned}\]草草草草草草草草怎么推出这么个东西?这太怪了……
不过这**实际上是对的。这题确实有这样的结论。
然后发现dp值只剩下两种,直接算就行了。
我以为这是换根dp,其实……
其实当我看到那个dp式子的时候就该反应过来它的意义 : 黑白染色,统计\(u\)子树内跟\(u\)同色点的个数。果然我是小拖拉机。