模拟赛考了一个轮廓线dp,然后输出样例走人……就爬来学了……
状压dp是什么
呃,就是当转移必须考虑前面做出的\(\omega(1)\)个决策的时候,把这些决策加入状态中进行转移。为什么是\(\omega(1)\)?因为\(O(1)\)的一般不叫状压dp。
基本的状态运算
二进制运算优先级,从高到低是 : ~最高,<<,>>其次,&再次,|最低。注意&,|的优先级低于比较运算符。
以下设\(S\)是全集。
补集 : a^S,S-a或~a&S,看个人喜好
交集 : a&b
并集 : a|b
\(a\)被\(b\)包含 : a|b==b或者a&b==a
遍历集合\(T\)的子集(不包含空集) :
1
2
for(int s=T;s;s=(s-1)&T)
//do something
遍历集合\(T\)的大小为\(k\)的子集 : 建议dfs。
有时候我们会用到三进制状压,这时候二进制的位运算就不那么好用了,不过我们有一种非常简单快速的方法就是爆搜预处理!
三进制状压一般不表示集合,所以一般不需要对状态各位做什么批量操作,只需要预处理出get[S][i]表示S的i位即可。当然对于状态集合大而稀疏的情况可以使用hash table或者离散化。
简单的例题
[SCOI2005] 互不侵犯
这个题非常经典啊!
考虑设\(dp(i,j,S)\)表示处理到第\(i\)行,已经放了\(j\)个国王,这一行状态为\(S\)的方案数。因为数据范围实在是小极了,可以直接枚举上一行状态来转移。
具体地,上一行跟这一行不冲突,等价于上一行、上一行左移一位、上一行右移一位之后都跟这一行没有交。
代码 :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<stdio.h>
int n,k;
long long dp[11][100][1000];
int popcnt[1000];
int main()
{
scanf("%d%d",&n,&k);
dp[0][0][0]=1;
for(int i=0;i<1<<n;i++)
popcnt[i]=popcnt[i>>1]+(i&1);
for(int i=1;i<=n;i++)
for(int j=0;j<=k;j++)
for(int S=0;S<1<<n;S++)
if(popcnt[S]<=j&&!((S<<1|S>>1)&S))
for(int T=0;T<1<<n;T++)
if(!((T|T<<1|T>>1)&S)) dp[i][j][S]+=dp[i-1][j-popcnt[S]][T];
long long ans=0;
for(int i=0;i<1<<n;i++)
ans+=dp[n][k][i];
printf("%lld",ans);
return 0;
}
[NOIP2017] 宝藏
过于经典!
考虑到这个树不是很好状压,但是实际上我们只需要知道一个点到根的距离,因此可以考虑bfs这棵树,我们设\(dp(i,S)\)表示当前考虑到第\(i\)层,已经开发的集合是\(S\)的最小代价,那么只需要枚举哪些点在第\(i\)层就可以了。这里状态数是\(O(n2^n)\)。
但是怎么知道这些点扩展出来的代价呢?考虑预处理\(g(S,T)\)表示从\(S\)走一层到\(T\)的最小代价,如果并不能这么走那就是-1。
复杂度?因为每个点只可能 : 在\(S\)中,在\(T\)中,都不在,所以状态数是\(O(3^n)\),那么总共就是\(O(n^23^n)\),大概是7e7,难度略大。
大吗?不大。因为常数实在是很小,还寻址连续,大概是可以跑过的。
转移的时候,枚举\(S\)的子集,然后使用预处理的转移来转移,复杂度可以用二项式定理分析,应该是\(O(n3^n)\)。总复杂度\(O(n^23^n)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<stdio.h>
#include<string.h>
const int inf=0x3f3f3f3f;
inline long long min(long long x,long long y){ return x<y?x:y; }
int n,m,e[20][20];
long long dp[13][4096],g[4096][4096];
int U;
int main()
{
scanf("%d%d",&n,&m);
U=(1<<n)-1;
memset(e,0x3f,sizeof(e));
for(int i=1,u,v,w;i<=m;i++)
scanf("%d%d%d",&u,&v,&w),e[v-1][u-1]=e[u-1][v-1]=min(e[u-1][v-1],w);
for(int S=0;S<=U;S++)
for(int T=S^U;T;T=(T-1)&(S^U))
for(int i=0;i<n;i++)
if(T&(1<<i))
{
int temp=inf;
for(int j=0;j<n;j++)
if(S&(1<<j))
temp=min(temp,e[j][i]);
g[S][T]+=temp;
}
for(int S=0;S<=U;S++) dp[0][S]=inf;
for(int i=0;i<n;i++) dp[0][1<<i]=0;
for(int i=1;i<=n;i++)
for(int S=0;S<=U;S++)
{
dp[i][S]=dp[i-1][S];
for(int T=S;T;T=(T-1)&S)
dp[i][S]=min(dp[i][S],dp[i-1][S^T]+i*g[S^T][T]);
}
printf("%lld",dp[n][U]);
return 0;
}
几种状态设计
非二进制状压
[CEOI2002] Bugs公司
给一个\(n\times m\)的矩阵,有一些位置有障碍,求放\(2\times 3\)或者\(3\times 2\)东西的方案数,\(n\leq 150,m\leq 10\)。
考虑三进制状压,\(dp(i,S)\)表示前\(i\)行,当前行状态为\(S\)的方案数,其中每一位表示这个格子上覆盖的东西,加上这一格还可以往下延伸的长度,如果没被覆盖就是0。预处理合法状态,dfs爆搜下一行可以放什么进行刷表转移。
轮廓线状压
轮廓线dp是一种状压dp,核心是把对后面决策有影响的轮廓线状压起来,其中轮廓线说的是已处理和未处理区域的分界线。一般用于在棋盘上摆东西的问题。
状压轮廓线上连通性的dp,也被称为插头dp。
对于一类行(列)之间转移复杂度带平方的状压dp可能有奇效,相当于是把枚举上/下一行的状态用另一个dp来优化,但是写起来并没有那么麻烦。
轮廓线是什么?它是已决策区域和未决策区域的分界线。
这里偷一张oi-wiki的图 :
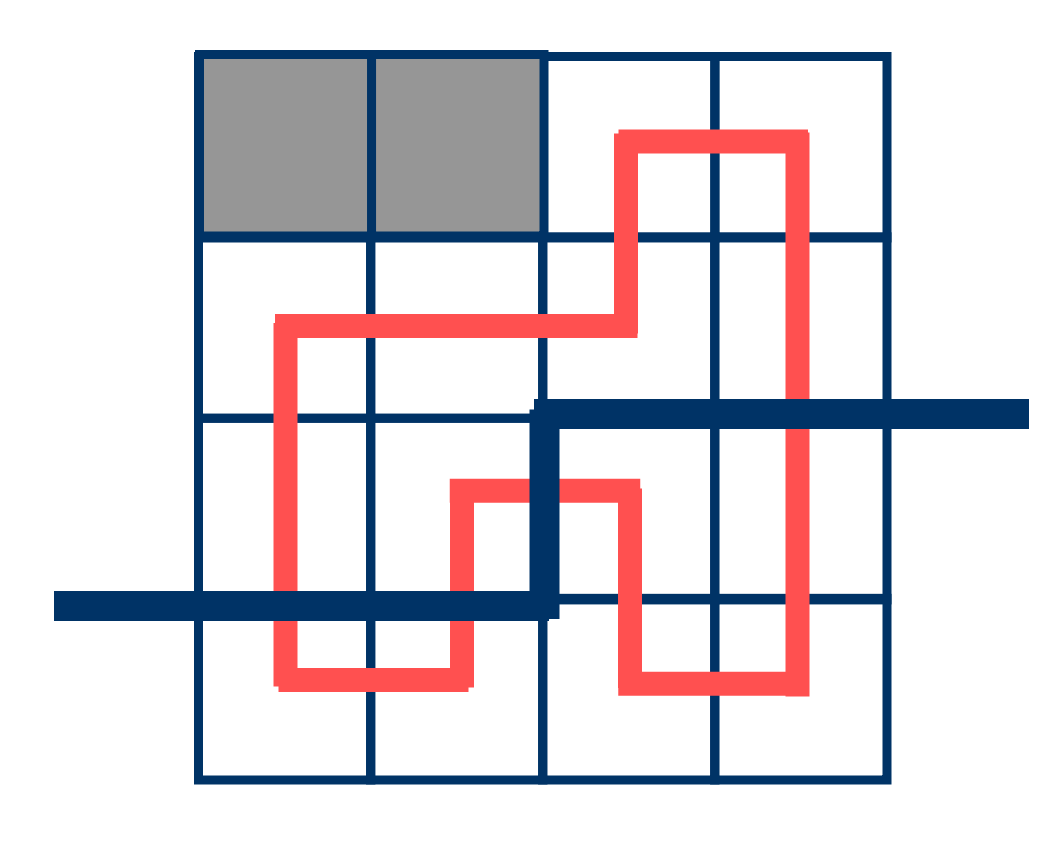
不要管那条红线(
如果我们从上往下、从左往右处理所有格子,那么那条粗线就是处理到第三行第三列时候的轮廓线。
状压轮廓线,说的就是把这条线上的有用信息,比如决策,状压起来方便转移。
hdu1400 Mondriaan’s Dream
太经典了!(好像每个题都很经典
题意 : 有一个\(n\times m\)的棋盘,保证大小是偶数,求往里面放满多米诺骨牌的方案数。
我们设\(dp(i,j,S)\)表示从上往下、从左往右处理到第\(i\)行第\(j\)列,已经放满了轮廓线上方所有格子,轮廓线下方的状态是\(S\)的方案数。其中\(S\)的状压方式是,第\(i\)位是\(1\)表示已经被放了(上方放了一个竖着的牌的上半部分),\(0\)表示没有被放。
如果\(S\)的第\(j\)位是\(1\),说明这个位置已经放了;否则说明它可以选择放不放,放还可以选择放一个横着的还是竖着的。转移可以使用刷表法。
没有代码(
一道模拟赛题
题意 : 咕咕咕。
总之就是斜着状压dp可以优化掉一个\(n\),当你可以斜着做的时候。
一些经典技巧
预处理可行状态
hdu1400 Mondriaan’s Dream 加强版
\(n\leq 10^9\)。
容易想到矩阵快速幂,我们可以把转移表示成矩阵,可是这个矩阵是\(2^{10}\times 2^{10}\)的啊?
发现很多状态是不合法的,具体地,连续的\(0\)数量不是偶数就不合法。这样状态数就会大幅减少,离散化一下,就可以通过了。
[NOI2001] 炮兵阵地
为了方便处理,我们先把行列反过来。
我们设\(dp(i,S_1,S_2)\)表示处理到第\(i\)行,这一行和上一行状态分别是\(S_1,S_2\)的方案数。
同样也有大量的不合法状态,可以预处理出合法状态。这题连离散化都不用(
也可以进行三进制状压dp,好像可以得到更好的速度,甚至更好的复杂度?不知道。
卡空间
[省选联考2020 A卷 D2T1/B卷 D2T2(应该是?)] 信号传递
首先信号传递的顺序是不重要的,所以可以预处理\(c_{i,j}\)表示\(i\)到\(j\)单向传递的次数。如果最后\(i\)在\(j\)左边那么\(i\)到\(j\)传递的贡献是\(c_{i,j}\),否则就是\(kc_{i,j}\)。
容易想到要贡献提前计算,考虑设\(dp(S)\)表示传完前面放着集合\(S\)里面的信号塔的最小代价,这个代价包括\(S\)内部的贡献和\(S\)对后面的贡献。
为了转移,我们预处理\(g(i,S)\),
\[g(i,S)=\sum_{j\in S}c_{i,j}\]这个可以很容易地对每个\(i\)递推获得(可以使用\(\mathrm{lowbit}\)来获取一个元素)。
那么我们枚举最后一个位置放了啥,有转移
\[dp(S)=\min_{i\in S}(dp(S-i)+g(i,U-S)+kg(i,S-i))\]然后你发现MLE 80pts。原因主要是\(g\)这个\(O(n2^n)\)太大了。
这里有很多方法卡这个空间,介绍最简单的一种。容易发现每个元素对\(g\)的贡献比较独立,我们考虑把\(g\)拆成\(g_1+g_2\),其中\(g_1\)考虑前\(12\)位,\(g_2\)考虑后\(11\)位,就给空间开了根号,而剩下的那个\(dp\)数组随便开也不会MLE。
啊事实上\(dp\)可以按\(\mathrm{popcnt}\)来滚,会优化掉一点空间,但是会增加极大的代码复杂度。
状态的最小表示和hash table
常用于头插dp,这种dp状态看起来巨大,但是实际上合法状态十分稀疏,同时还不很容易预处理合法状态。
等我学了头插dp再补。
头插dp
咕咕咕。