ddp通过把转移写成矩阵的形式来证明结合律并简单地合并转移。一般情况下,由于转移具有结合律并可以快速合并,我们使用线段树等数据结构来维护转移,从而解决带修改或range query的简单dp问题。
广义矩阵乘法,两个基本定理
首先我们要定义广义矩阵乘法。设\(\oplus,\otimes\)是两种运算,那么定义两个矩阵\(A,B\)的广义矩阵积\(C\)为 :
\[c_{i,j}=\bigoplus_{k=1}^{l}a_{i,k}\otimes b_{k,j}\]当然这里\(A\)是\(n\times l\)的矩阵,\(B\)是\(l\times m\)的矩阵,\(C\)就是\(n\times m\)的矩阵。
定理1 如果\(\otimes,\oplus\)都有结合律,并且\(\otimes\)对\(\oplus\)有分配律,那么这个广义矩乘也满足结合律。自证不难,爆力展开即可。
常见的一些有\(\oplus=\min/\max,\otimes=+\),结合律显然,分配律就是\(\min(a,b)+c=\min(a+c,b+c)\)。
还有\(\oplus=\mathrm{xor},\otimes=\mathrm{and}\),暴力计算可以证明对于\(01\)的情况是有分配律的,因此这个东西对于任意位也满足分配律。注意\(\mathrm{or}\)和\(\mathrm{xnor}\)并没有这么好的性质。
定理2 还是上面的条件,那么这个广义矩乘满足矩阵加法对矩阵乘法的分配律,或者说\((A\times B)\oplus(A\times C)=A\times(B\oplus C)\)。当然这里加法也是\(\otimes\)意义下的。自证也不难。
这个可以把一些”矩阵乘完什么东西之后加起来”变成”矩阵加起来再乘什么东西”,合并转移矩阵的时候可能用到(,虽然我没用过)。
左乘右还是右乘左
看你应用变换的顺序。我一般喜欢拿转移矩阵左乘dp数组进行转移,对于左乘的话,意义是从右往左应用变换。
对于从左往右转移的序列ddp,我们一般反着乘,也就是把左儿子的矩阵放在右边乘,因为左儿子的变换先被应用。从右往左转移则要正着乘。
对于以子树为阶段的树上ddp,如果采用dfn+hld的话,我们一般是正着乘,因为左儿子的变换后被应用;如果采用静态lct,也是正着乘。
序列上的ddp
CF618E Robot Arm
显然可以把每一节表示成一个平移,那么我们只要写出矩阵然后复合就好了。
注意到每次旋转会同时转后面所有的,这个可以通过旋转的差分来解决(旋转同时有交换律),更好的办法是从后往前应用线性变换,这样前面的旋转就可以作用于后面了。
单点修改区间最大子段和
题意 : 单点修改,区间最大子段和。
设\(dp_i\)为右端点为\(i\)的最大子段和,\(ans_i\)为只考虑前\(i\)个的答案,可以写出如下的转移 :
\[\begin{aligned} dp_i&=\max(dp_{i-1}+a_i,a_i)\\ ans_i&=\max(ans_{i-1},dp_i) \end{aligned}\]写成矩阵乘法的形式,就是
\[\begin{bmatrix} a_i&-\infty&a_i\\ a_i&0&a_i\\ -\infty&-\infty&0 \end{bmatrix} \begin{bmatrix} dp_{i-1}\\ ans_{i-1}\\ 0 \end{bmatrix} = \begin{bmatrix} dp_i\\ ans_i\\ 0 \end{bmatrix}\]不知道哪里来的题的加强版
题意 : 有一堆人要按某种顺序给你投票。每个人有一个理想评分\(a_i\)(当然可以是负数),如果他投票的时候,你得到的分数\(<a_i\),他会给你点+1;如果\(>a_i\)则点-1,如果\(=a_i\)则什么也不做。一开始每个人的理想评分都是\(0\),你需要支持修改一个人的理想评分,或者查询 如果你可以随便安排顺序,最多可以得到多少分。
贪心地,容易发现按理想评分从小到大排是最优的,然后容易发现得分变化是一开始一串连续的-1,接下来全是+1或不变。考虑我们分开讨论,对于第一段可以二分出 理想评分 和 一直-1的得分 的交点,第二段可以写成ddp的形式。如果我们设\(f_i\)表示前\(i\)个人打完之后的得分,那么有
\[f_i=\min(f_{i-1}+1,a_i)\]所以可以写出转移矩阵
\[\begin{bmatrix} 1&a_i\\ \infty&0\\ \end{bmatrix} \begin{bmatrix} f_{i-1}\\ 0 \end{bmatrix} = \begin{bmatrix} f_i\\ 0 \end{bmatrix}\]开一棵值域线段树维护即可。
CF750E New Year and Old Subsequence
考虑这是一个子序列自动机上乱蹦的模型,所以先画个自动机出来。
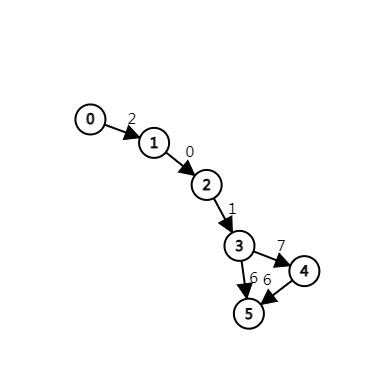
考虑设\(f_{i,j}\)表示考虑了前\(i\)个字符,走到自动机上的结点\(j\)至少需要删多少字符。
分别考虑四种字符,那么可以写出超大的转移矩阵(认为\(0\times\infty=0\)) :
\[\begin{bmatrix} 0 & \infty[a_i=6] & \infty[a_i\neq 6] & \infty & \infty & \infty\\ \infty & [a_i=6] & \infty[a_i\neq 7] & \infty & \infty & \infty\\ \infty & \infty & [a_i\in\{6,7\}] & \infty[a_i\neq 1] & \infty & \infty\\ \infty & \infty & \infty & [a_i=1] & \infty[a_i\neq 0] & \infty\\ \infty & \infty & \infty & \infty & [a_i=0] & \infty[a_i\neq 2]\\ \infty & \infty & \infty & \infty & \infty & [a_i=2]\\ \end{bmatrix} \begin{bmatrix} f_{i-1,5}\\ f_{i-1,4}\\ f_{i-1,3}\\ f_{i-1,2}\\ f_{i-1,1}\\ f_{i-1,0} \end{bmatrix} = \begin{bmatrix} f_{i,5}\\ f_{i,4}\\ f_{i,3}\\ f_{i,2}\\ f_{i,1}\\ f_{i,0} \end{bmatrix}\]注意这里因为是静态问题,使用矩阵乘向量可以大大减小常数。
树上的ddp
洛谷P4719 【模板】”动态 DP”&动态树分治
树上的ddp是什么呢?它一般用来解决一些从儿子们转移来的dp,当然它能解决的不止这些。
众所周知HLD之后树就是重链+轻边,重链上我们可以用序列上的ddp解决,而轻儿子的贡献就需要考虑一下。
树上的最大权独立集大家都会求。
考虑链上的问题,或者说序列上的问题,设\(f_{u,0/1}\)表示\(u\)子树内\(u\)选/不选的答案。假设现在\(u\)只有一个重儿子\(v\),那就有 :
\[\begin{bmatrix} 0&0\\ a_u&-\infty \end{bmatrix} \begin{bmatrix} f_{v,0}\\ f_{v,1} \end{bmatrix} = \begin{bmatrix} f_{u,0}\\ f_{u,1} \end{bmatrix}\]考虑菊花上的问题,如果一个点有一堆儿子,那么我们把儿子们的转移矩阵分别乘初始向量,得到的结果都加起来就好了。所以我们得到一个垃圾算法 : 从每个叶子开始,拿着初始向量乘这个点的矩阵,然后在每个结点处把儿子们的向量加起来。这个做法实在是太垃圾了,因为我们只会合并向量而不会合并矩阵!
换个想法,我们把轻儿子的转移并入父亲,设\(g_{u,0/1}\)表示强制不选/选\(u\),只考虑轻儿子的答案,枚举轻儿子\(v\),容易发现有 :
\[\begin{aligned} g_{u,0}&=\sum_{v}\max(f_{v,0},f_{v,1})\\ g_{u,1}&=\sum_{v}f_{v,0} \end{aligned}\]设重儿子是\(v\),于是可以得到这样的转移 :
\[\begin{bmatrix} g_{u,0}&g_{u,0}\\ g_{u,1}&-\infty \end{bmatrix} \begin{bmatrix} f_{v,0}\\ f_{v,1} \end{bmatrix} = \begin{bmatrix} f_{u,0}\\ f_{u,1} \end{bmatrix}\]考虑修改产生的影响,重链上的影响容易处理,对于每个重链头向上连的轻边,我们用重链头的转移矩阵乘初始向量得到重链头的dp值,然后去更新重链头的父亲的\(g\)。复杂度是\(O(n\log^2 n)\)。
洛谷P4751 【模板】”动态DP”&动态树分治(加强版)
把hld+线段树换成静态lct即可。
[SDOI2017] 切树游戏
显然是个背包。设\(f_{u,i,k}\)表示\(u\)为根,只考虑前\(i\)个儿子,权值为\(k\)的连通块方案数。令\(f_{u,k}\)表示考虑所有儿子的答案。设第\(i\)个儿子是\(v\),显然有转移
\[f_{u,i,k}=f_{u,i,k}+\sum_{j=0}^{m-1}f_{u,i-1,j}f_{v,k\space\mathrm{xor}\space j\space\mathrm{xor}\space a_u}\]直接做是单次\(O(nm^2)\)的。发现是个异或卷积(把\(k\)变成\(k\space\mathrm{xor}\space a_u\)就完全是那个形式了),于是可以用fwt优化到\(O(nm\log m)\)。还可以一上来就全fwt一遍,直接用fwt后的结果进行计算,最后fwt回来,应该是\(O(nm\log m)-O(nm+m\log m)\)的。本质是fwt-xor是个线性变换,类似的fwt-and/or以及fft也是线性变换。
说起来这里要是写成生成函数会很简单,但是好像没有广为人知的这一类东西的书写规范?不管了。
我们定义异或卷积意义下的生成函数\(F(z)\),使得它的乘法满足异或卷积的规则。
我们令\(F_u\)表示点\(u\)为根的答案数组的生成函数。继续设\(G_u\)表示把\(u\)的轻儿子们的\(F+1\)全异或卷积卷起来的结果(\(+1\)表示不选的决策)。
为了统计答案,设\(Ans_u\)表示\(u\)子树里的\(F\)之和,\(H_u\)表示\(u\)轻儿子们的\(ans\)之和。
如果设\(v\)是\(u\)的重儿子,那么有
\[\begin{aligned} F_u&=z^{a_u}G_u(F_v+1)\\ Ans_u&=H_u+Ans_v+F_u\\ &=H_u+Ans_v+z^{a_u}G_uF_v+z^{a_u}G_u \end{aligned}\]于是可以写出一个转移矩阵
\[\begin{bmatrix} z^{a_u}G_u & 0 & z^{a_u}G_u\\ z^{a_u}G_u & 1 & H_u+z^{a_u}G_u\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} F_v\\ Ans_v\\ 1\\ \end{bmatrix} = \begin{bmatrix} F_u\\ Ans_u\\ 1\\ \end{bmatrix}\]那么我们就可以愉快地上ddp板子了!复杂度\(O((n+q)m\log^2 n)\)。
不过有个小问题 : 更新链头对父亲的贡献时,需要先除去原来的贡献;如果计算过程中遇到了10007的倍数,那么我们没法进行除法。
这可以通过维护10007倍数的出现次数来搞定。具体地,我们乘/除10007的倍数的时候,并不真的去改变数值,而是开一个计数器计算已经乘了的10007倍数的个数。乘则给计数器+1,除则-1。要求实际值的时候,如果计数器非0那么值是0,否则是不考虑10007倍数得到的数值。注意这题空间限制并不松,如果被卡空间可以考虑使用short类型。
不过还有个小问题 : 这东西常数太**大了。\(3\times 3\)的矩阵,每个位置都是数组,常数可想而知。
如果你尝试一下或者打个表,你会发现这个转移矩阵的矩乘在形式上具有封闭性,换句话说
\[\begin{bmatrix} a_1 & 0 & b_1\\ c_1 & 1 & d_1\\ 0 & 0 & 1\\ \end{bmatrix}\begin{bmatrix} a_2 & 0 & b_2\\ c_2 & 1 & d_2\\ 0 & 0 & 1\\ \end{bmatrix} =\begin{bmatrix} a_1a_2 & 0 & a_1b_2+b_1\\ c_1a_2+c_2 & 1 & c_1b_2+d_1+d_2\\ 0 & 0 & 1\\ \end{bmatrix}\]不过发现初始向量并不是这样的形式,它的第三行第一列是个\(1\)而不是\(0\)。我们可以考虑硬拆开看一看转移矩阵和初始向量乘出来是什么东西,发现有
\[\begin{bmatrix} a & 0 & b\\ c & 1 & d\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 1\\ \end{bmatrix} = \begin{bmatrix} b\\ d\\ 1\\ \end{bmatrix}\]所以实际上我们只需要维护四个元素,矩乘的常数从\(27\)次乘法,\(27\)次加法变成了\(4\)次乘法,\(4\)次加法,块多了。
适当封装写起来还是很舒服的!只不过我写了近240行(。可以在这里看到。
洛谷上这题有两组毒瘤数据,常数不小的话只有LCT/静态LCT可以跑过去,于是我还写了一份静态LCT的版本。这个复杂度是\(O((n+q)m\log n)\)。