Rank-Pairing Heap(rp-heap,赋级配对堆)是一种堆。(废话
复杂度和Fib堆相同(如果不知道Fib堆什么复杂度,百度,请)。
论文里说rp堆更优秀(理由是维护的信息更少),但wiki说Fib堆更快一些。
不过至少我觉得rp-heap要好写得多(论文里好像也这么说了)。毕竟我这种菜鸡都能写出来
还有EtaoinWu的《配对堆与赋级配对堆(Rank Pairing Heaps)》。本文的大部分中文译名参考自此。
先膜为敬,EtaoinWu Orz
本文中采用中文还是英文名似乎很混乱。
写blog不易,给个赞吧(
以下默认是最小堆(小根堆)。
前置知识 : 二叉树,渐进记号,摊还分析,初中一年级数学(废话
不必要的前置知识 : 配对堆,二项堆,Fib堆
说几句闲话,学习Fib堆可以参考洛咕谷日爆报 :
#214[木木!]安塔的二项堆&斐波那契堆学习笔记
但是个人认为这篇文章讲得不够详细(就连势函数都是不完整的),如果想详细了解,还是推荐算法导论,或者这篇blog。
想要代码的话,LOJ的最短路板子按代码长度排序,第一页有两个Fib堆实现,分别是lcomyn的373378和qiyue7的187001。在上面那篇日报评论区和那个blog里也有。看出来Fib堆难写了
0.一些记号
$H$表示一个rp-heap,$x,y$表示结点或数值,$key$表示关键字。
$\operatorname{left}$和$\operatorname{right}$分别表示左儿子和右儿子。
$\operatorname{insert}(x,H)=\operatorname{merge}(\operatorname{make-heap}(x),H)$
$\operatorname{delete}(p,H)=\operatorname{decrease-key}(p,-\inf,H),\operatorname{extract-min}(H)$
文中提到”其它操作复杂度”时,不包括以上两操作的复杂度。
1.半树(half tree)
1.1.定义
rp-heap是由若干半树($\text{half tree}$)组成的。
$\text{half-ordered}$的定义是 : 每个结点的$key$比左子树任意结点的$key$小。
半树的定义是 : 根节点没有右儿子,且所有点满足$\text{half-ordered}$性质的二叉树。(请仔细读这句话
由此可以立刻得出根是树中最小的。
1.2.$\operatorname{link}$
$\operatorname{link}$是半树的基本操作,用于把两棵半树合并成一棵半树。它的过程如下 :
$\operatorname{link}$接受两棵半树的根$x,y$作为输入。不妨假设$x$的$key$更小。把$x$的左儿子拿下来,接到$y$的右儿子上,然后把$y$接到$x$的左儿子上。这是$O(1)$的。
这是从论文里拿的图 :
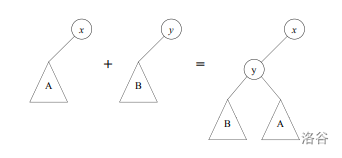
显然合并后仍然满足半树定义。
1.3.$\operatorname{rank}$(级)
定义$\operatorname{rank}:V \to \mathbb{N}$。单个节点的$\operatorname{rank}$是$0$。定义一棵半树的$\operatorname{rank}$是根的$\operatorname{rank}$值。
我们规定,$\operatorname{rank}$值相同的半树能进行$\operatorname{fair-link}$。操作之后,具有较大$key$的根$\operatorname{rank}+1$,其它结点不变。还是从论文拿的图 :
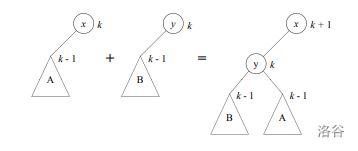
发现如果从若干只有一个结点的半树开始,不管怎样$\operatorname{fair-link}$,产生的半树的形态都是根的左子树挂着一个满二叉树。
更进一步,发现这样的半树跟二项树本质是相同的。画个图解释一下 :
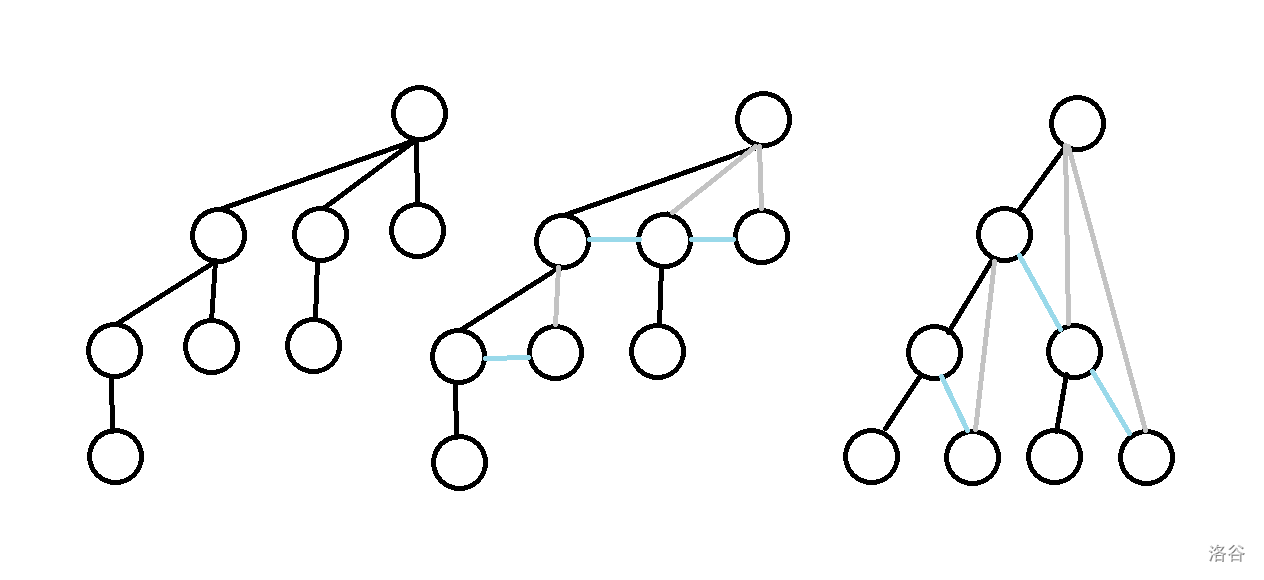
(希望dalao们可以给我一个能做这样动图的软件qwq)
所以这个数据结构可以看作二项堆的优化。(Fib堆似乎也是qwq)
实际上论文似乎就是这么认为的。
但由于复杂度分析里面用到了半树上的兄弟,使用二项树的理论可能会很难受。
2.rp-heap的结构
rp-heap使用一个称为根链表的双向循环链表串起一串的半树根(但是实际上根链表存在仅仅是为了方便插入删除,并不表示任何顺序),并且维护堆中有着最小值的结点的指针$H.min$。显然,$H.min$一定是某个根。
3.一个不够优秀的复杂度
对于$\operatorname{merge}$和$\operatorname{insert}$,我们直接连接/插入根链表。
对于$\operatorname{extract-min}$,和二项堆一样,把$H.min$删掉后,把它左子树的右链(或右脊柱,即从根一直走右儿子直到没有右儿子得到的路径)上所有边断开,得到若干棵半树(因为每个点都满足$\text{half-ordered}$,并且断开右链后右链上的点失去了右儿子)。将这个操作称为$\operatorname{disassembly}$(拆分)。
接下来把这些半树和根链表里的其它根一起进行一轮配对($\text{One-pass link}$) : 对每个$\operatorname{rank}$建立一个桶,先遍历$\operatorname{disassembly}$产生的半树根再遍历根链表,把当前半树扔进对应的桶里。如果桶里已经有树,把它们$\operatorname{fair-link}$起来,并删掉根链表里面两棵树的根,直接在根链表加入$\operatorname{link}$后的新根。最后把桶里剩下的也扔进根链表。
对于$\operatorname{decrease-key}$,为了达到$O(1)$,我们用被减值的结点$x$的右子树替换它原来的位置,把它和它的左子树拿出来扔到根链表里,这个操作称为对$x$的一次$\operatorname{cut}$(切断)。这样我们才能不必让$x$上浮。
但是它破坏了$\operatorname{rank}$为$r$的二项树至少有$2^r$个结点的性质(你把一部分拆出来了,结点数就不够了),因此可以造出$\operatorname{rank}$达到$\omega(\log n)$的半树,这样$\operatorname{extract-min}$就需要使用$\omega(\log n)$个桶。
这个东西可以摊到除了$\operatorname{extract-min}$是$O(\log n)$的(没有$\operatorname{decrease-key}$的情况下),其它都是$O(1)$的,即不带$\operatorname{decrease-key}$的Pairing Heap复杂度。因为我看不懂英文这不是重点,所以这里不给出证明。有兴趣可以自行阅读论文。
为了得到高效的$\operatorname{decrease-key}$,我们需要放宽一些限制,使$\operatorname{rank}$是$O(\log n)$的性质不会被$\operatorname{decrease-key}$打破后难以复原,并在优秀的实现中保持该性质。
4.一个优秀的复杂度
定义$\Delta \operatorname{rank}(x)=\operatorname{rank}(\operatorname{fa}(x))-\operatorname{rank}(x)$,称左儿子$\Delta \operatorname{rank}$为$i$的点为一个$i$-结点,两个儿子$\Delta \operatorname{rank}$分别为$i,j$(不分顺序)的点为一个$i,j$-结点。
在之前的做法和标准的二项堆里,每个根是$1$-结点,每个内部结点是$1,1$结点。rp-heap的核心思想是放宽内部结点的限制。
我们引入两种$\text{rank rule}$,它们是rp-heap对半树$\operatorname{rank}$的限制。
Type-1(甲类)条件 : 每个根是$1$-结点,而每个内部结点要么是$1,1$-结点,要么是$0,?$-结点,其中$?$是任意正整数。可以发现一棵满足Type-1条件的$\operatorname{rank}$为$r$的半树至少有$2^r$个结点。
Type-2(乙类)条件 : 每个根是$1$-结点,而每个内部结点是$1,1$-结点,$1,2$-结点或$0,?$-结点,其中$?$是任意正整数。可以发现一棵满足Type-2条件的$\operatorname{rank}$为$r$的半树至少有$\text{Fibonacci}_ {r+2}\geq\phi^r$个结点。
因此不管使用哪一种$\text{rank rule}$,最大$\operatorname{rank}$是$O(\log n)$的。
这不会影响前面其它操作的正确性。
接下来我们可以尝试实现$\operatorname{decrease-key}$了。
如果被减值结点$x$是根,不用做任何结构操作。
否则,先对$x$进行一次$\operatorname{cut}$,并把$\operatorname{rank}(x)$设为$\operatorname{rank}(\operatorname{left}(x))+1$。然后从$x$原来的父亲开始,判断当前结点是否仍然满足$\text{rank rule}$,如果不满足,则把当前结点的$\operatorname{rank}$减少到满足,并继续处理当前结点的父亲。如果没有破坏条件就结束。
这是论文中的图 : (图中是Type-1 rp-heap)
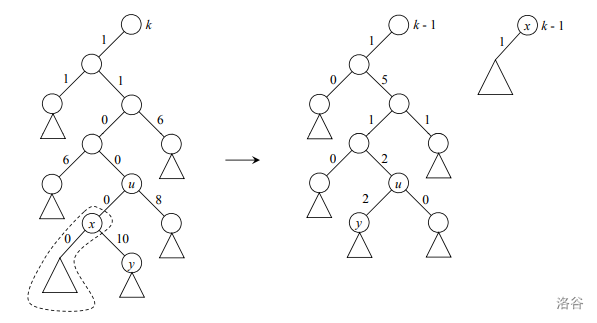
现在你知道这个数据结构名字的由来了,它使用类似于配对堆的配对方式,并用特殊的$\text{rank rule}$来放松二项堆对结点$\operatorname{rank}$的限制,从而得到优秀的复杂度。
Fib堆也用到了类似的思想 : 在Fib堆里,如果一个结点要破坏使$\operatorname{extract-min}$复杂度正确的性质时,就把它也拆下来,并把拆下来这部分的复杂度摊掉。一会你将看到,rp堆也会摊掉保持$\text{rank rule}$的代价。
说句闲话,看看进度条
5.复杂度分析
下面的内容比较毒瘤并且有很多显然,请自行选择是否看完。不想看可以向下翻到代码部分。
这里只分析常数更小的Type-2 rp-heap。对Type-1有兴趣的话,反正我不会请自行阅读论文。
定义一个结点$u$的基本势($\text{base potential}$)为,设$u$是一个$i,j$-结点($u$只有一个儿子则视$j=0$),则基本势为$i+j-1$,即$\Delta \operatorname{rank}(\operatorname{left}(u))+\Delta \operatorname{rank}(\operatorname{right}(u))-1$。
(这个译名是我口胡的,如果不标准,希望神仙们可以指出来)
定义一个结点$u$的额外势($\text{extra potential}$)为 :
-
如果$u$是根,额外势为$1$。
-
如果$u$是$1,1$-结点,额外势是$-1$。
-
否则,额外势是$0$。
(这个译名也是我口胡的,如果不标准,也希望神仙们可以指出来)
定义一个结点$u$的势为基本势和额外势的和。则立刻可得 :
-
如果$u$是根,势为$1$。
-
如果$u$是$1,1$-结点,势为$0$。
-
否则,设$u$是$i,j$-结点,势为$i+j-1$。
定义势函数为所有结点势的和。
$\operatorname{merge}$和$\operatorname{find-min}$实际代价是$O(1)$的并且不改变势。$\operatorname{make-heap}$和$\operatorname{insert}$实际代价是$O(1)$的并且将势增加$1$。所以这四个操作摊还复杂度都是$O(1)$。
考虑$\operatorname{extract-min}$。定义$h$为$\operatorname{disassembly}$后半树的总数。显然,$\operatorname{extract-min}$的实际代价是$O(h+\log n)$($\log n$是操作桶的时间,如果你每次最后遍历桶而不是记录非空桶的话)。考虑被删除根的左子树右链上最多有$\log_{\phi} n$个$1,1$-结点(每个使$\operatorname{rank}$减少$1$),它们变成根之后会增加最多$\log_{\phi} n$的势。除此之外其它任何结点变成根都不会使势增加,所以$\operatorname{disassembly}$使势增加最多$\log_{\phi} n$。接下来进行一轮配对,在这$h$棵半树中最少进行$(h-\log_{\phi}n-1)/2$次$\operatorname{fair-link}$,每一次会把一个根变成$1,1$-结点,使势减少$1$,因此配对至少使势减少$(h-\log_{\phi}n-1)/2=h/2-O(\log n)$。整个操作使势增加最多$\log_{\phi}n-(h/2-O(\log n))=O(\log n)-h/2$。我们可以把势的单位增加到可以消去实际代价$O(h)$,因此摊还复杂度是$O(\log n)$。
接下来是恶心的$\operatorname{decrease-key}$。假设我们对$x$做了一次减值。
如果$x$是根,实际代价是$O(1)$并且不改变势。
否则,我们就懒得往下分析了 定义$u_0=\operatorname{left}(x), u_1=x, u_i=\operatorname{fa}(u_{i-1})(1<i\leq k)$且$u_k$为在$\operatorname{decrease-key}$中维持$\text{rank rule}$时遇到的第一个不需要调整就满足$\text{rank rule}$的结点或是根(为根时是调整了根或根的儿子),定义$v_i$为$\operatorname{decrease-key}$前$u_i$除$u_{i-1}$之外的儿子,即$u_{i-1}$的兄弟。加$\mathrm{‘}$表示$\operatorname{decrease-key}$后的(真省事)(就是说,举个例子,$\operatorname{rank}$是$\operatorname{decrease-key}$前的$\operatorname{rank}$,$\operatorname{rank’}$是$\operatorname{decrease-key}$后的$\operatorname{rank}$)。
显然,这次操作的实际代价是$O(k)$。
显然,$\operatorname{decrease-key}$后势可能发生变化的只有$u_1,…,u_k$。
显然,$\operatorname{decrease-key}$后的结构变化只有$u_2$的原来是$u_1$的那个儿子变成了$v_1$,$u_1$变成了根并失去了右儿子。
先考虑基本势变化,即$u_1,…,u_k$的基本势变化。把它分成三部分。我们会在每部分最后列出一个式子,从它们可以推出关于基本势变化的结论。
-
考虑$v_1,u_1,u_2,…,u_{k-1}$的$\Delta \operatorname{rank}$和,在$\operatorname{decrease-key}$前它们在同一条链上,中间的部分拆开相消,得到$\operatorname{rank}(u_k)-\operatorname{rank}(v_1)$。
(说句闲话,这部分论文似乎出了点问题,把$v_1$写成了$v_0$)
考虑$v_1,u_2,u_3,…,u_{k-1}$的$\Delta \operatorname{rank’}$和,在$\operatorname{decrease-key}$后它们在同一条链上,中间的部分拆开相消,得到$\operatorname{rank’}(u_k)-\operatorname{rank’}(v_1)$。
因为$\operatorname{rank’}(v_1)=\operatorname{rank}(v_1)$且$\operatorname{rank’}(u_k)\leq\operatorname{rank}(u_k)$,$\operatorname{rank’}(u_k)-\operatorname{rank’}(v_1)\leq\operatorname{rank}(u_k)-\operatorname{rank}(v_1)$。这部分的基本势减少了至少$0$。(这是$u_i$对$u_{i+1}$的贡献,$\operatorname{decrease-key}$前$v_1$对$u_1$的贡献和$\operatorname{decrease-key}$后$v_1$对$u_2$的贡献)
-
显然,$\Delta\operatorname{rank’}(u_0)=1\leq\Delta\operatorname{rank}(u_0)+1$。这部分的基本势减少了至少$0$。(这是$u_0$对$u_1$的贡献)
-
因为$u_i$被调整了而$v_i$没有,$\Delta\operatorname{rank’}(v_j)\leq\Delta\operatorname{rank}(v_j)-1(2\leq j< k)$。因为$u_k$不一定被调整了,$\Delta\operatorname{rank’}(v_k)\leq\Delta\operatorname{rank}(v_k)$。这部分的基本势减少了至少$k-3$。(这是$v_i$对$u_i(2 \leq i)$的贡献)
我们已经计算了$u_1,…u_k$的每个儿子对它们的贡献。把它们加起来就得到基本势减少了至少$k-3$,即增加最多$3-k$。
然后考虑额外势变化。考虑额外势只会在$1,1$-结点变成其它结点时,或是某个结点变成根时增加$1$。
我们先证明在被调整的点中最多只有两个$1,1$-结点。考虑调整过程中遇到的第一个$1,1$-结点$u_j$,它会被调整为$1,2$-结点或$0,?$-结点。对于第一种,它的$\operatorname{rank}$没有改变,所以父亲的条件不会被破坏,所以它是最后一个被调整的结点,一共有一个$1,1$-结点。对于第二种,它的$\operatorname{rank}$减少了$1$,因此接下来所有需要调整点的$\operatorname{rank}$都只会减少$1$(不理解可以自己枚举情况)。接下来遇到的第二个$1,1$-结点只会被调整为$1,2$-结点,所以它是最后一个被调整的结点,一共有两个$1,1$-结点。因此,$1,1$-结点最多有两个,最多使额外势增加$2$。
在$\operatorname{decrease-key}$过程中,只有$u_1$变成了根,使额外势增加$1$。
把基本势和额外势的变化加起来,我们得到势的变化 : 势最多增加$6-k$。我们可以把势的单位增大到可以消去实际代价$O(k)$,所以$\operatorname{decrease-key}$的摊还复杂度是$O(1)$。
6.代码实现
请参考放在最前面的EtaoinWu的blog。
或者往下翻,是我自己写的代码,有注释。用指针没有可读性
优化Dijkstra到$O(n \log n+m)$是支持$O(\log n)$时间$\operatorname{insert}$和$\operatorname{extract-min}$,$O(1) \space\operatorname{decrease-key}$的堆的经典应用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
//Type-2 Rank-Pairing Heap优化Dijkstra
//luogu P4779(请自行调整MAXN和MAXM)
//没有merge操作,写起来大概也不难(
#define MAXN 100000
#define MAXM 1000000
#define Log_Phi_N 29
//点数,边数,桶数量
#ifndef NULL
#define NULL 0
#endif
#include<string.h>
#include<stdlib.h>
#include<stdio.h>
template<class T>
struct RP_Heap
{
struct ListNode;
struct Node
{
T val;
int rank;
Node *l,*r,*fa;
ListNode* p;
Node(){}
Node(T _val,int _rank=0,Node* _l=0,Node* _r=0,Node* _fa=0):val(_val),rank(_rank),l(_l),r(_r),fa(_fa){}
}t[MAXN+2],*p[MAXN+2],*min,*bucket[Log_Phi_N+1];
int cnt,siz;
bool has_min;
struct ListNode
{
Node* ptr;
ListNode *pre,*nxt;
};
struct List//手写链表
{
ListNode* head;
List()
{
head=new ListNode();
head->ptr=NULL;
head->nxt=head;
head->pre=head;
}
inline void insert(Node* _ptr)
{
ListNode* u=new ListNode();
u->ptr=_ptr;
u->pre=head;
u->nxt=head->nxt;
head->nxt->pre=u;
head->nxt=u;
_ptr->p=u;
}
inline void remove(ListNode* u)
{
u->pre->nxt=u->nxt;
u->nxt->pre=u->pre;
u->ptr->p=NULL;
delete u;
}
}list;
RP_Heap()
{
for(int i=0;i<MAXN;i++)
p[i]=&t[i];//p[i]指向t[i],便于分配空间
has_min=0;//has_min让extract-min之后不用把min赋为-inf
memset(bucket,0,sizeof(bucket));
}
inline Node* new_Node(T v)//这句话就是分配一个新结点,val为v的意思(
{
return ( & ( * p[cnt++] = Node(v,0,NULL,NULL,NULL) ) );
}
inline void swap(int &x,int &y){ int temp=x;x=y;y=temp; }
inline int max(int x,int y){ return x>y?x:y; }
inline int abs(int x){ return x>0?x:-x; }
inline void swap(Node* &x,Node* &y){ Node* temp=x;x=y;y=temp; }
inline Node* link(Node* u,Node* v)
{
if(v->val<u->val) swap(u,v);
v->r=u->l;
if(v->r)//记得判断是不是空指针,否则RE,以下类似的省略注释
v->r->fa=v;
u->l=v;
v->fa=u;
u->rank++;
return u;
}
inline Node* update_min(Node* u)//更新min,为了写起来舒服,返回值是给的指针
{
if(!has_min||u->val<min->val)
min=u,has_min=1;
return u;
}
inline Node* insert(T _val)
{
Node* u=new_Node(_val);
list.insert(update_min(u));//看出来update_min这么写舒服了qwq
siz++;
return u;
}
inline T find_min(){ return min->val; }
inline int size(){ return siz; }
inline bool empty(){ return siz==0; }
inline void extract_min()
{
siz--;
list.remove(min->p);
has_min=0;
int rk;
Node *next_node,*u;
ListNode *first=list.head->nxt;//第一个原有根位置
for(u=min->l;u;u=next_node)//拆分左子树右链
{
next_node=u->r;
u->fa=u->r=NULL;
rk=u->rank;
if(bucket[rk])//和桶里的合并,扔进根链表
list.insert(update_min(link(u,bucket[rk]))),bucket[rk]=NULL;
else//扔进桶
bucket[rk]=u;
}
for(ListNode *i=first,*next_node;i!=list.head;i=next_node)
{
u=i->ptr;
rk=u->rank;
next_node=i->nxt;
list.remove(i);
if(bucket[rk])
list.insert(update_min(link(u,bucket[rk]))),bucket[rk]=NULL;
else
bucket[rk]=u;
}
for(int i=0;i<=Log_Phi_N;i++)//遍历桶,把桶里的扔进根链表
if(bucket[i])
list.insert(update_min(bucket[i])),bucket[i]=NULL;
}
inline void decrease_key(Node* u,T key)//把u的值变成k(所以需要自己保证是减值不是增值)
{
u->val=key;
if(u->fa==NULL)//是根,更新min直接返回
{
update_min(u);
return;
}
if(u->l) u->rank=u->l->rank+1;//更新rank为左儿子rank+1
else u->rank=0;//没有左儿子,说明是单点
if(u->r) u->r->fa=u->fa;//把右儿子接到自己原来的位置
if(u==u->fa->l) u->fa->l=u->r;
else u->fa->r=u->r;
int temp,lrk,rrk;
for(Node* v=u->fa;v;v=v->fa)
{
lrk=v->l?v->l->rank:-1;//实现的小技巧,没有结点的rank视为-1
rrk=v->r?v->r->rank:-1;
temp=max(lrk,rrk)+(abs(lrk-rrk)<=1?1:0);//根据rank rule计算新的rank
if(temp==v->rank)//如果没有改变rank,break掉
break;
v->rank=temp;
}
u->fa=u->r=NULL;//最后断开父亲和右儿子是因为前面循环开头要用右儿子,懒得再搞临时变量了
list.insert(update_min(u));//插入根链表并更新min
}
};
//下面的是Dijkstra模板
struct Edge
{
int v,w,next;
}e[2*MAXM+2];
struct Node
{
int u;
int dis;
inline bool operator<(const Node &x) const
{
return this->dis<x.dis;
}
};
int h[MAXN+2],cnt=0;
inline void add_edge(int u,int v,int w)
{
e[++cnt]={v,w,h[u]};
h[u]=cnt;
}
int dis[MAXN+2];
int n,m,start,tu,tv,tw,to;
RP_Heap<Node> q;
RP_Heap<Node>::Node* node[MAXN+2];//对每个堆结点保留一个指针,才能进行decrease-key
inline void dij()//Dijkstra板子
//没有vis(表示是否已经扩展过的数组)是因为我们有decrease-key
{
int now;
for(int i=1;i<=n;i++)
dis[i]=i==start?0:0x7fffffff,node[i]=q.insert({i,dis[i]});
while(!q.empty())
{
now=q.find_min().u;
q.extract_min();
for(int i=h[now];i!=0;i=e[i].next)
if(dis[e[i].v]>dis[now]+e[i].w)
dis[e[i].v]=dis[now]+e[i].w,
q.decrease_key(node[e[i].v],{e[i].v,dis[e[i].v]});//减值
}
}
int main()
{
scanf("%d%d%d",&n,&m,&start);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&tu,&tv,&tw),add_edge(tu,tv,tw);
dij();
for(int i=1;i<=n;i++)
printf("%d ",dis[i]);
return 0;
}
7.说在后面&更新记录
看到这篇blog的dalao们,如果发现了什么问题,希望可以告诉我qwq
2020/4/15 完结撒花qwq
upd 2020/4/16: 增加了代码,修改了一些细节。
upd 2020/4/17: 修改了一些细节。连更三天可见有多少bug
upd 2020/4/22: 修改了一处错误。
upd 2020/5/22: 修改了一些细节。
upd 2020/9/20: 修改了一处错误。