胡乱说几句

Saying

我在打gen/fn ——数学皇冠上的明珠 wky

这句话说的很好，但是当你尝试理解，你会感到wky老师的神力。

数论是什么

数论主要研究整数的性质。

一个约定

提到模数的时候，用$m$表示任意数，$p$表示素数。

一句闲话

如果你掉线了，请在翻过一页之后立刻尝试重连。

整除，素数，$\gcd$，互素，整值函数

这些大家应该都接触过了。

几个我们将会用到的定义和性质

$n\bmod{k}=n-k\left\lfloor\frac{n}{k}\right\rfloor$

$\left\lfloor\frac{\left\lfloor\frac{n}{a}\right\rfloor}{b}\right\rfloor=\left\lfloor\frac{n}{ab}\right\rfloor$

素数筛，唯一分解

筛指的是求解关于$1,...,n$中具有某种性质的数的问题的算法。

有些时候我们需要求出$1,...,n$的所有素数，此时我们需要素数筛。

埃氏筛

最简单的素数筛。我们从$2$开始从小到大考虑每个数，如果一个数是素数，则标记它的所有倍数不是素数。如果扫到一个数的时候，它还没被标记，那么它必然是素数。

复杂度是$O(n\log\log n)$。这里给出一个感性的分析，假设素数是随机分布的，根据素数定理，$k$有$\frac{1}{\ln k}$的概率是素数，并且如果它是，则会贡献$\frac{n}{k}$的代价。所以复杂度就是$\displaystyle n\int_2^n\frac{1}{x\ln x}\mathrm{d}x$之类的，积出来就是$n\ln\ln n$。理性分析存在，但是比较复杂，大家可以自己百度一下。

线性筛

线性筛把复杂度优化到线性，其核心是考虑每个合数都可以表示成它的最小素因子乘上另一个数，我们在枚举到那另一个数的时候把它筛掉，这样每个数只会筛掉一次。

具体一点，我们从小到大枚举，假设现在枚举到$i$，那么再枚举一个已经扫过的素数$p$，把$ip$标记为合数。然后如果$i$中含有一个$p$，我们就该停下来了，因为继续进行的话，比如枚举到$p^\prime$，那么$ip^\prime$的最小素因子就不是$p^\prime$了，而是$p$。

素数定理

$n$以内的素数个数$\pi(n)=\Theta(\frac{n}{\log n})$。更精确地，$\pi(n)\sim\frac{n}{\ln n}$。

唯一分解定理

每个数有且仅有一种方式分解成若干个素数的乘积。

证明比较显然。首先归纳一下显然每个数都有至少一种方式分解。

考虑如果一个数有两种方式分解成若干个素数的乘积，那么约掉两种方式中都出现了的素数，我们就得到一些素数乘起来等于另一些素数，并且这两个素数集合都非空且不交。

考虑一个素数的性质，实际上它是素数的另一种定义 : 如果$p\mid ab$，那么必然有$p\mid a$或$p\mid b$，一会我们会证明这个。

于是如果这两个集合分别是$p_1,p_2,...$和$q_1,q_2,...$，那么必然有$p_1\mid q_1q_2...$，而素数都是互素的，所以必然有$p_1=q_i$，但是刚才我们已经约干净了，所以就矛盾了。

计算唯一分解

一个数超过根号的素因数最多有一个。我们枚举$\leq\sqrt{n}$的素数去除，然后如果剩下的部分不是$1$，它必然是一个超过根号的素因数。

轮子筛(spoj PRIMES2)

可以在$O(\frac{n}{\log\log n})$内筛出前$n$个素数。

考虑我们取前$k$个素数，设它们的乘积是$L$，那么$n$和$n+L$是否被这$k$个素数整除的情况是相同的，所以我们考虑把$kL+1,...,(k+1)L$作为一段处理，这看起来就像用一个长$L$的轮子滚过数轴。

取最大的$k$使得$L\leq\sqrt{n}$，素数定理分析一下可以知道$k$是$\Theta(\log n)$的。

mertens定理指出这$L$个数里面有$O(\frac{L}{\log k})$个数不被前$k$个素数整除，也就是说我们一共有$O(\frac{n}{\log k})=O(\frac{n}{\log\log n})$个数还没被筛掉。

这些还没筛掉的数就是所有最小素因数在$k+1$个及以后的素数。我们只用$k+1$及以后的素数，在这些数里面跑一个线筛，复杂度就是$O(\frac{n}{\log\log n})$。

扩展欧几里得算法(exgcd)

最简单的欧几里得算法用于求解$\gcd(a,b)$。

这个太拉了。我们给出结论 : 对于不都是$0$的整数$a,b$，必然存在整数$x,y$，满足$ax+by=\gcd(a,b)$，这称为Bezout(裴蜀/贝祖)定理。

接下来描述如何用欧几里得算法计算$x,y$，以及证明这个结论和算法本身的正确性。

考虑我们现在知道了$bx+(a\bmod{b})y=\gcd(a,b)$的解，展开然后对照一下 :

接下来我们进行证明。它求出的解显然确实满足$ax+by=g$，只需要证明$g$确实是$\gcd(a,b)$。

首先$ax+by$必然是$\gcd(a,b)$的倍数，所以我们求出的$g$必然是$\gcd(a,b)$的倍数。

于是自然考虑如何证明它也是$\gcd(a,b)$的因数。注意到它必然同时是$a,b$的因数，因为它同时是$b,a\bmod{b}$的因数，而$a\bmod{b}=a-kb=a-k^\prime\gcd(a,b)$。

所以我们同时证明了结论$\gcd(a,b)=\gcd(b,a\bmod{b})$。

回去证明在唯一分解定理里面用到的结论，也就是如果$p\mid ab$，则$p\mid a$或$p\mid b$。

如果$p\not\mid a$，那么由于$p$是素数，必然有$p\perp a$，所以存在$x,y$满足$px+ay=1$，所以$b=b(px+ay)=bpx+bay$。由于$p\mid ab$，所以必然有$p\mid b$。

随便切几个

乘法逆元

给$a,b$，求$ax\equiv 1\pmod{b}$。

等价于$ax-by=1$，所以解一组，然后取$x\bmod{b}$即可。

一般来说我们会膜素数，此时有费马小定理$a^{p-1}\equiv 1\pmod{p}$，所以可以快速幂。

在你不需要比较大小的时候，逆元的性质和倒数非常接近，你可以大胆使用它。在答案是有理数的计数问题中很容易见到它。

exCRT

给$a_1,m_1,a_2,m_2$，求$x\equiv a_1\pmod{m_1},x\equiv a_2\pmod{m_2}$的通解。

考虑一些简单的情况，容易感觉到通解具有$x\equiv a\pmod{m}$的形式，其中必然有$m\equiv\operatorname{lcm}(m_1,m_2)$。

两个式子分别改写成$x=a_1+k_1m_1,x=a_2+k_2m_2$，于是$k_1m_1-k_2m_2=a_2-a_1$，解可以得到一组$k_1,k_2$，然后就可以得到$x$。

试看看!

线性逆元

给一个序列$a$和模数$m$，保证$a_i\perp m$，求其中每一项的逆元。$n\leq 10^7,m\leq 10^9$，不要管怎么读入。

hint : 我们只需要对整个序列的乘积求一次逆元。

求出整个序列乘积的逆元$b$，跑前后缀积$\mathrm{pre},\mathrm{suf}$，那么$a_i$的逆元就是$b\mathrm{pre}_i\mathrm{suf}_i$。

thupc2018 密码学第三次小作业

给$a_1,a_2,e_1,e_2,m$，其中$e_1\perp e_2$且$m$只有两个素因数，求解$x^{e_1}\bmod{m}=a_1,x^{e_2}\bmod{m}=a_2$，保证答案中$x\perp m$。$v<2^{64}$。

hint : $e_1\perp e_2$和$x^1$有啥关系?

解出$e_1i+e_2j=1$，那么我们要求的就是$x^{e_1i+e_2j}=a_1^ia_2^j$。但是$i,j$可能是负数，不过发现如果$x\perp m$的话，$a_1,a_2$必须也$\perp m$，所以求个逆就好了。

noio22 pj B. 数学游戏

给$z,x$，解$z=xy\gcd(x,y)$。$v\leq 2^{63}$。

考虑一个素因子$p$的幂次，我们得到$z=x+y+\min(x,y)$。也就是说现在我们知道$x,z,z-x=y+\min(x,y)$，要求$y$。

讨论就行了。当$x\leq y$，我们得到$z=y+x,y=z-x$。当$x\geq y$，我们得到$z=2y,y=\frac{z}{2}$。考虑如何才能搞出一个东西，它在$x\leq y$的时候得到$z-x$，在$x\geq y$的时候得到$\frac{z}{2}$。

这个$\frac{1}{2}$看起来不是很好，我们最后开根号，问题变成凑一个$2z-2x,z$。

考虑它看起来像是这样的 :

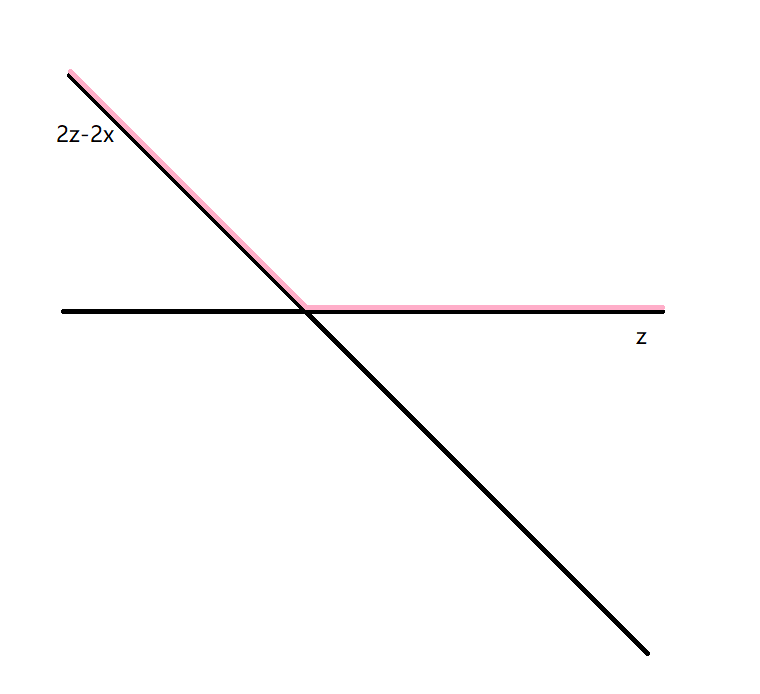
所以我们所要的东西就是$\max(2z-2x,z)$。答案就是$\sqrt{\operatorname{lcm}(\frac{z^2}{x^2},z)}$，但是$x$不一定整除$z$ ，所以我们把它改成$\displaystyle\sqrt{\frac{z\operatorname{lcm}(z,x^2)}{x^2}}$，就结束了。

求和

整除分块

求$\sum_{i=1}^n\lfloor\frac{n}{i}\rfloor$。

注意到$\lfloor\frac{n}{i}\rfloor$只有$O(\sqrt{n})$种不同的取值。如果$i\leq\sqrt{n}$，那么只有根号个$i$；如果$i\geq\sqrt{n}$，那么$\frac{n}{i}\leq\sqrt{n}$，于是只有根号个$\lfloor\frac{n}{i}\rfloor$。实际上取值个数确实几乎是$2\sqrt{n}$。

由于它是单调的，我们知道相同的取值肯定是连续的一段。为了找到每一段，可以考虑二分，复杂度$O(\sqrt{n}\log n)$。

为了砍$\log$，我们需要$O(1)$求一段的端点。考虑如果这一段的$\lfloor\frac{n}{i}\rfloor=d$，那么也就是$d\leq\frac{n}{i}< d+1$，于是$\frac{n}{d+1}< i\leq\frac{n}{d}$，于是这一段的右端点就是$\lfloor\frac{n}{d}\rfloor$。各种整除分块都可以如此分析。

cqoi2007 余数求和

求$\displaystyle\sum_{i=1}^nk\bmod{i}$。

模板 整除分块。

根据定义，$k\bmod{i}=k-i\lfloor\frac{k}{i}\rfloor$，所以答案就是$\displaystyle nk-\sum_{i=1}^ni\lfloor\frac{k}{i}\rfloor$。

注意到$\lfloor\frac{k}{i}\rfloor$只有根号段，每一段中都可以把它提出来，剩下的问题就是求$i$的区间和，可以$O(1)$。

经典数论函数

狄利克雷卷积

定义$h=f\ast g$为$\displaystyle h(n)=\sum_{d\mid n}f(d)g(\frac{n}{d})$。

在只考虑一个素数的所有幂时，狄利克雷卷积即为普通卷积。

这导出贝尔级数，不过我还是比较喜欢dgf，不过这都是闲话了。

简单函数

定义$\mathrm{id}_k(n)=n^k,\mathbf{1}(n)=1,\epsilon(n)=[n=1]$。

$\mu$

$\mu$定义为容斥系数$\mu\ast\mathbf{1}=\mathrm{id}$。从低往高递推容易知道$\mu$是存在且唯一的。

接下来尝试直接获得$\mu$的值。唯一分解定理实际上说明了每个素数表示一个维度。可以猜测，如果我们构造一组函数$q_i(n)$满足只考虑所有$p_i^k$的时候它能完成容斥$q_i\ast\mathbf{1}=\mathrm{id}$，则把所有$q_i$狄利克雷卷积起来就得到$\mu$。

刚才我们说过只考虑一个素数的所有幂时，狄利克雷卷积即为普通卷积，而此时卷上$\mathbf{1}$的意义就是做前缀和。容易感觉到或算出$q_i$是差分$q_i(1)=1,q_i(p_i)=-1$，其它取值都为$0$。

所以我们把它们合起来，就得到$\mu(n)$的值 : 如果$n$所有的非零次素因数次数都是$1$，则$\mu(n)=(-1)^{\omega(n)}$，其中$\omega$是素因数个数；否则，也就是说有出现次数超过$1$的素因数，则$\mu(n)=0$。爆力可以验证它确实满足$\mu\ast\mathbf{1}=\mathrm{id}$。

如果一个函数像$\mu$这样是各个素因数幂的函数值乘起来，或者说它对各素数是独立的，那么就称它为积性的。等价定义是如果$a\perp b$，那么$f(ab)=f(a)f(b)$。

显然$\mathbf{1},\mathrm{id}$也是积性的。并且，它们不光对各素数独立，对一个素数的每次出现也是独立的，也就是说它的那个$q_i$满足$q_i(p_i^k)=q_i^k(p_i)$，或者说它不要求$a\perp b$也有$f(ab)=f(a)f(b)$。这样的函数称为完全积性的。

$\varphi$

$\varphi$定义为$n$以内和$n$互素的数的个数。

$\varphi$的等价定义是系数$\varphi\ast\mathbf{1}=\mathrm{id}$，容易感觉到它也是积性的。

我们如法炮制，从第二种定义获得$\varphi$的值。卷$\mathbf{1}$相当于前缀和，所以可以感觉到它是$\mathrm{id}$的差分$q_i(p_i^k)=p_i^k-p_i^{k-1}$。

然后我们证明这确实是$n$以内和$n$互素的数的个数。可以发现$n\perp m$等价于$n$包含的每个素数都$\perp m$，证明考虑Bezout定理，$nx+my=1$，如果我们对每个素因数$p$构造了$px+my=1$，那么给每个方程乘上$\frac{n}{p}$就可以构造$nx+my=1$，而如果存在$p\mid n$满足$p\not\perp m$，必然也有$n\not\perp m$。

可以看出Bezout定理是用一个方程描述了互素，让难以直接处理的数论性质变得比较容易进行代数操作了。

考虑一个数和$n$的素因数$p$互素，当且仅当它不是$p$的倍数。为了计算不被任何$n$的素因数整除的数的个数，考虑容斥，钦点一个素因数集合$S$，设它里面素因数们的乘积是$c(S)$，则有$\frac{n}{c(S)}$个数被它们同时整除，所以我们知道答案就是$\displaystyle\sum_S(-1)^{\vert S\vert}\frac{n}{c(S)}$，也就是$\displaystyle n\sum_S\prod\limits_{p\in S}\left(-\frac{1}{p}\right)$。注意到这是一个多项式定理，它就是$\displaystyle n\prod_p\left(1-\frac{1}{p}\right)$，展开可以知道它和我们刚才推出的东西是相等的。

$d$

$d$定义为$n$的因数个数，包括$1$和它本身。$1$的因数个数是$1$。

$d$是积性的。考虑$d$是$n$的因数，当且仅当$d$在每一个素数上次数都$\leq n$的次数，所以如果$n$分解之后各次数分别是$e_1,e_2,...$，那么$d(n)=\prod(e_i+1)$。

考虑如何求$d$的前缀和，也就是$\sum_{i=1}^nd(i)$。

注意到它就是$\sum_{i=1}^n\left\lfloor\frac{n}{i}\right\rfloor$，整除分块即可。

存在$O(n^{\frac{1}{3}}\log n)$计算它的方法，可以搜索divcnt1。

莫比乌斯反演

(noi2010 能量采集)转化后是求$\displaystyle\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)$，$n,m\leq 10^5$。

看我推式子。

如果代入$\varphi\ast 1=\mathrm{id}$呢

看我推式子。

可以发现这个题里面进行代换的目的就是交换求和号，因为$\gcd(i,j)$对$i,j$不独立，但是$d\mid\gcd(i,j)$对$i,j$独立，它就等价于$d\mid i,d\mid j$。

yy的gcd

求$\displaystyle\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)\text{ is prime}]$，$n,m\leq 10^7$，$10^4$组询问。

看我推式子。

可以线筛我们所要的东西。更好的方法是使用线性积性函数狄利克雷卷积。

线性狄利克雷卷积

我们爆力计算素数幂，然后线筛得到所有数处的值。

后半部分是线性，而前半部分复杂度是$\sum\limits_p\log_p^2 n$。

考虑$\leq\sqrt{n}$的$p$，它们的贡献总和不超过$\sqrt{n}\log^2 n$。$\geq\sqrt{n}$的$p$，它们的$\log_p n\leq 2$，所以总和是$\frac{n}{\ln n}$。

试看看!

luogu6222 简单题 加强版

给$k$，每次询问给$n$，求$\displaystyle\sum_{i=1}^n\sum_{j=1}^n\gcd(i,j)\mu^2(\gcd(i,j))$，$n\leq 10^7$，$10^4$组询问。

和yy的gcd一样做。

luogu4240 毒瘤之神的考验

求$\displaystyle\sum_{i=1}^n\sum_{j=1}^m\varphi(ij)$，$n,m\leq 10^5$，$10^4$组询问。

hint : $\varphi(ij)=\frac{\varphi(i)\varphi(j)\gcd(i,j)}{\varphi(\gcd(i,j))}$。

看我推式子。

当我们有两个做法的时候，根号分治。

$\mu^2$

求$\displaystyle\sum_{i=1}^n\mu^2(i)$，$n\leq 10^{12}$，$1000$组询问。

hint : $\mu^2(n)=1$等价于$n$无平方因子。

hint : $n$无平方因子等价于$n$的最大平方因子是$1$，对它莫反。

看我推式子。

于是可以做到$O(n^{\frac{1}{2}})-O(n^{\frac{1}{3}})$。

一些别的

bsgs

给$a,b,p$，求解$a^x\equiv b\pmod{p}$。

考虑折半，取$B=\Theta(\sqrt{p})$，把$x$分解为$x=iB-j$，方程变为$(a^B)^i\equiv ba^j\pmod{p}$。左边有根号种，右边有根号种，预处理一边塞进hash table，枚举另一边查询。

lucas

求$\binom{n}{m}\bmod{p}$，$n,m\leq 10^{18},p\leq 10^6$，$10^5$组询问。

lucas定理指出$\binom{n}{m}\equiv\binom{\lfloor n/p\rfloor}{\lfloor m/p\rfloor}\binom{n\bmod{p}}{m\bmod{p}}\pmod{p}$。递归即可，复杂度$O(\log_p n)$。

kummer

(cf582D Number of Binominal Coefficients)给$p^e,L$，求$k\leq n\leq L$且$p^e\mid\binom{n}{k}$的$n,k$对数。$p,e\leq 10^9,L<10^{1000}$，答案膜$10^9+7$。

kummer定理指出$\displaystyle\nu_p\left(\binom{a+b}{a}\right)$就是$p$进制下$a$加上$b$时进位的次数，或者$a+b$减去$a$时退位的次数。

考虑$\displaystyle\nu_p((a+b)!)-\nu_p(a!)-\nu_p(b!)=\sum_k\left(\left\lfloor\frac{a+b}{p^k}\right\rfloor-\left\lfloor\frac{a}{p^k}\right\rfloor-\left\lfloor\frac{b}{p^k}\right\rfloor\right)$，可以发现右边这个描述的就是每一位是否进位。

考虑数位dp。设$dp(i,j,0/1,lim)$表示前$i$位，已经进位了$j$次，低位没有/有进位，$a+b$是否卡上限的方案数。转移的时候钦点下下位是否进位，如果这一位还卡着则决策下一位是否还卡着，如果卡着下一位是确定的，把这个和分到$a,b$里面即可；如果不卡着则随意分配，只要进位情况对就行，两个方案数显然都可以$O(1)$计算。复杂度$O(\log^2 L)$。

exEuler

(cf906D Power Tower)序列和一个数$m$，每次查询一个区间$l,...,r$，求$a_l^{a_{l+1}^{a_{l+2}^{...}}}\bmod{m}$。$n,q\leq 10^5$。

对底数我们可以直接取膜，但是对指数不行。比如大家都知道费马小定理$a^{p-1}\equiv 1\pmod{p}$，也就是在膜素数下给指数取膜要膜$p-1$。

exEuler定理指出，$a^n\bmod{m}=a^{\varphi(m)+n\bmod{\varphi(m)}}\bmod{m}$。注意到奇数的$\varphi$是偶数，而偶数的$\varphi$折半，所以$\log$次之后就没了，爆力即可，复杂度$O(q\log^2 v)$。

Euler定理指出，如果$a\perp m$，那么$a^n\bmod{m}=a^{n\bmod{\varphi(m)}}\bmod{m}$。

试看看!

如果有时间就讲的题。

hdu5848 hdu多校16 D9 E. Easy Homework 弱化版 弱化版 加强版

给$a,x,p,l,r,f_0,f_1,f_n$，求膜$p$下以$f_0,f_1$为首项的fib数列的区间$[l,r]$中值$f_n$的出现次数。$a,p\leq 10^9,l,r\leq 10^{18}$，保证$5$是膜$p$的二次剩余。

hint : fib数列膜任意数必然纯循环。如果$5$是膜$p$的二次剩余，并且循环节是$p-1$的因数。你可以通过枚举一个$p-1$的因数然后矩阵快速幂来计算循环节长度。

hint : 卡西尼恒等式 : $f_{n+1}f_{n-1}-f_n^2=(-1)^{n-1}(f_0^2+f_1f_0-f_1^2)$，可以通过考虑fib数的转移矩阵得到。

hint : cipolla算法可以$O(\log v)$对一个数开平方根，现在假设你可以随意使用它。

通过卡西尼恒等式和递推式，我们可以解二次方程得到$\displaystyle f_{n-1}=\frac{-f_n\pm\sqrt{f_n^2+4(f_n^2+(-1)^n)}}{2}$，枚举$n$的奇偶性可以得到四个$f_{n-1}$。

考虑bsgs。fib数的转移矩阵设为$M$，初值是$\mathrm{x}$，我们解出来的是$\mathrm{y}$，则有$M^k\mathrm{x}=\mathrm{y}$。可以bsgs解出一次循环中$\mathrm{y}$出现的所有位置，于是对四种可能的$\mathrm{y}$分别解一下就得到$f_n$在这个循环中出现的所有可能位置，于是容易统计答案。

loj6222 幂数！ 加强版 加强版

定义powerful number是它的每个素因数都$\geq 2$次的数。求$n$以内powerful number的$k$次方和。$n\leq 10^{30},k=O(1)$，2s。

hint : 我们需要第一步转化得到一个阳间一点的式子。一个数$n$是powerful number，当且仅当它可以表示成$n=a^2b^3$，其中$\mu^2(b)=1$。

答案即为$\displaystyle\sum_{i=1}^{\lfloor\sqrt[3]{n}\rfloor}\mu^2(i)i^{3k}\sum_{j=1}^{\left\lfloor\sqrt{\frac{n}{i^3}}\right\rfloor}j^{2k}$。化一化。

也就是$\displaystyle\sum_{i^3j^2d^6\leq n}(i^3j^2d^6)^k\mu(d)$。

外层枚举$i$，对$j$整除分块，$d$不超过$O(n^{\frac{1}{6}})$，可以爆力预处理。$j$的整除分块，取值只有$O(n^{\frac{1}{5}})$种，总复杂度$O(n^{\frac{1}{5}})$。

luogu4466 集训队互测2012 和与积

求$a,b\leq n$，且$a+b\mid ab$的$a,b$对数，也就是$\displaystyle\sum_{i=1}^n\sum_{j=1}^n[a+b\mid ab]$。$n<2^{31}$。

hint : 我们需要第一步转化得到一个阳间一点的式子。

考虑使用$d=\gcd(a,b)$来表示这个限制。改写成$[id+jd\mid ijd^2]$，也就是$[i+j\mid ijd]$。

注意到$i\perp j$，所以$\gcd(ij,i+j)=\gcd(i,i+j)\gcd(j,i+j)=1$。也就是说$[i+j\mid ijd]=[i+j\mid d]$。也就是说我们转化成了计算三元组$i,j,d$的数量，需要满足$i>j,i\perp j,id\leq n$这样的。看我推式子。

接下来我们先考虑枚举$k,i$的做法。

然后考虑枚举$i,i+j$的做法。

Saying again

我在打gen/fn ——数学皇冠上的明珠 wky

这句话说的很好，但是当你尝试理解，你会感到wky老师的神力。

Thanks for Listening!

感谢数学皇冠上的明珠 wky的指导。洛谷关注wkywkywky喵，关注wkywkywky谢谢喵!

Powered by reveal.js